hdu4389 X mod f(x)[数位dp]

X mod f(x)

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 3020    Accepted Submission(s): 1182

Problem Description

Here is a function f(x):
　　　int f ( int x ) {
　　　    if ( x == 0 ) return 0;
　　　    return f ( x / 10 ) + x % 10;
　　　}

　　　Now, you want to know, in a given interval [A, B] (1 <= A <= B <= 10⁹), how many integer x that mod f(x) equal to 0.

 

Input

　　　The first line has an integer T (1 <= T <= 50), indicate the number of test cases.
　　　Each test case has two integers A, B.

 

Output

　　　For each test case, output only one line containing the case number and an integer indicated the number of x.

 

Sample Input

2 1 10 11 20

 

Sample Output

Case 1: 10 Case 2: 3

 

Author

WHU

 

Source

2012 Multi-University Training Contest 9

 

Recommend

zhuyuanchen520   |   We have carefully selected several similar problems for you:  4385 4383 4388 4387 4386 

 

由于f(x)最大就是81，所以可以算对于1-81每一个数都求一下就可以

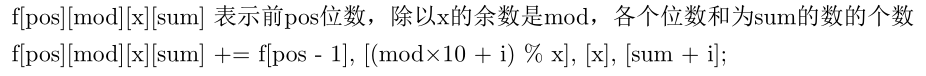
#include<cstdio>
#include<cstring>
using namespace std;
int cas,T,bits[20];
int f[11][82][82][82];
int dfs(int pos,int mod,int x,int sum,bool lim){
    if(!pos){return x==sum&&!mod;}
    int &res=f[pos][mod][x][sum],ans=0;
    if(!lim&&(~res)) return res;
    int up=!lim?9:bits[pos];
    for(int i=0;i<=up;i++){
        ans+=dfs(pos-1,(mod*10+i)%x,x,sum+i,lim&&i==bits[pos]);
    }
    if(!lim) res=ans;
    return ans;
}
int solve(int x){
    int len=0;int ans=0;
    for(;x;x/=10) bits[++len]=x%10;
    for(int fx=1;fx<=81;fx++) ans+=dfs(len,0,fx,0,1);
    return ans;
}
int main(){
    int l,r;
    memset(f,-1,sizeof f);
    for(scanf("%d",&T);T--;){
        scanf("%d%d",&l,&r);
        printf("Case %d: %d
",++cas,solve(r)-solve(l-1));
    }
    return 0;
}