Oh My Holy FFF
Time Limit: 5000/2500 MS (Java/Others) Memory Limit: 65535/65535 K (Java/Others)
Total Submission(s): 1047 Accepted Submission(s): 291
Problem Description
N soldiers from the famous "*FFF* army" is standing in a line, from left to right.
You, as the captain of *FFF*, want to divide them into smaller groups, but each group should still be continous in the original line. Like this:
In your opinion, the number of soldiers in each group should be no more than L.
Meanwhile, you want your division be "holy". Since the soldier may have different heights, you decide that for each group except the first one, its last soldier(which is the rightmost one) should be strictly taller than the previous group's last soldier. That is, if we set bi as the height of the last soldier in group i. Then for i >= 2, there should be bi > bi-1.
You give your division a score, which is calculated as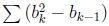 , b0 = 0 and 1 <= k <= M, if there are M groups in total. Note that M can equal to 1.
, b0 = 0 and 1 <= k <= M, if there are M groups in total. Note that M can equal to 1.
Given the heights of all soldiers, please tell us the best score you can get, or declare the division as impossible.
o o o o o o o o o o o o o o o o o o
/F /F /F /F /F /F /F /F /F /F /F /F /F /F /F /F /F /F
/ / / / / / / / / / / / / / / / / /
You, as the captain of *FFF*, want to divide them into smaller groups, but each group should still be continous in the original line. Like this:
o o o | o o o o | o o o o o o | o o o o o
/F /F /F | /F /F /F /F | /F /F /F /F /F /F | /F /F /F /F /F
/ / / | / / / / | / / / / / / | / / / / /
In your opinion, the number of soldiers in each group should be no more than L.
Meanwhile, you want your division be "holy". Since the soldier may have different heights, you decide that for each group except the first one, its last soldier(which is the rightmost one) should be strictly taller than the previous group's last soldier. That is, if we set bi as the height of the last soldier in group i. Then for i >= 2, there should be bi > bi-1.
You give your division a score, which is calculated as
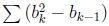 , b0 = 0 and 1 <= k <= M, if there are M groups in total. Note that M can equal to 1.
, b0 = 0 and 1 <= k <= M, if there are M groups in total. Note that M can equal to 1.Given the heights of all soldiers, please tell us the best score you can get, or declare the division as impossible.
Input
The first line has a number T (T <= 10) , indicating the number of test cases.
For each test case, first line has two numbers N and L (1 <= L <= N <= 105), as described above.
Then comes a single line with N numbers, from H1 to Hn, they are the height of each soldier in the line, from left to right. (1 <= Hi <= 105)
For each test case, first line has two numbers N and L (1 <= L <= N <= 105), as described above.
Then comes a single line with N numbers, from H1 to Hn, they are the height of each soldier in the line, from left to right. (1 <= Hi <= 105)
Output
For test case X, output "Case #X: " first, then output the best score.
Sample Input
2
5 2
1 4 3 2 5
5 2
5 4 3 2 1
Sample Output
Case #1: 31
Case #2: No solution
Source


#include<cstdio> #include<cstring> #include<algorithm> #include<iostream> #define lc k<<1 #define rc k<<1|1 using namespace std; typedef long long ll; const int N=1e5+5; struct node{ll a,p;}d[N]; int n,T,L,cas;ll f[N];ll mx[N<<2]; void change(int k,int l,int r,int p,ll v){ if(l==r){mx[k]=v;return ;} int mid=l+r>>1; if(p<=mid) change(lc,l,mid,p,v); else change(rc,mid+1,r,p,v); mx[k]=max(mx[lc],mx[rc]); } ll query(int k,int l,int r,int x,int y){ if(l==x&&r==y) return mx[k]; int mid=l+r>>1; if(y<=mid) return query(lc,l,mid,x,y); else if(x>mid) return query(rc,mid+1,r,x,y); else return max(query(lc,l,mid,x,mid),query(rc,mid+1,r,mid+1,y)); } bool operator <(const node &x,const node &y){ return x.a!=y.a?x.a<y.a:x.p>y.p; } void work(){ ll nv,pre; scanf("%d%d",&n,&L); for(int i=1;i<=n;i++) scanf("%I64d",&nv),d[i].a=nv,d[i].p=i; sort(d+1,d+n+1); memset(f,-1,sizeof f); fill(mx,mx+(n<<2),-1); change(1,0,n,0,0); for(int i=1,ni;i<=n;i++){ ni=d[i].p; nv=d[i].a; pre=query(1,0,n,max(0,ni-L),ni-1); if(pre>=0){ f[ni]=pre+nv*nv; change(1,0,n,ni,f[ni]-nv); } if(ni==n) break; } if(f[n]>0) printf("%I64d ",f[n]); else puts("No solution"); } int main(){ for(scanf("%d",&T);T--;){ printf("Case #%d: ",++cas);work(); /*for(int i=1;i<=n;i++) scanf("%d",a+i); for(int i=1;i<=n;i++){ for(int j=max(0,i-L);j<i;j++){ if(a[i]>a[j]){ f[i]=max(f[i],f[j]+a[i]*a[i]-a[j]); } } } if(!f[n]) puts("No solution"); else printf("%d ",f[n]);*/ } return 0; }