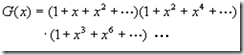找单词
Problem Description
假设有x1个字母A, x2个字母B,..... x26个字母Z,同时假设字母A的价值为1,字母B的价值为2,..... 字母Z的价值为26。那么,对于给定的字母,可以找到多少价值<=50的单词呢?单词的价值就是组成一个单词的所有字母的价值之和,比如,单词 ACM的价值是1+3+14=18,单词HDU的价值是8+4+21=33。(组成的单词与排列顺序无关,比如ACM与CMA认为是同一个单词)。
Input
输入首先是一个整数N,代表测试实例的个数。
然后包括N行数据,每行包括26个<=20的整数x1,x2,.....x26.
Output
对于每个测试实例,请输出能找到的总价值<=50的单词数,每个实例的输出占一行。
Sample Input
2 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 9 2 6 2 10 2 2 5 6 1 0 2 7 0 2 2 7 5 10 6 10 2 10 6 1 9
Sample Output
7 379297
这道题的算法是母函数。
先解释下母函数
n称函数G(x)是序列a0,a1,a2,…的母函数
(1+x)n是序列C(n,0),C(n,1),...,C(n,n)的母函数。
如若已知序列a0,a1,a2,…则对应的母函数G(x)便可根据定义给出。反之,如若已经求得序列的母函数G(x),则该序列也随之确定。
序列a0,a1,a2,…可记为{an} 。
例1:若有1克、2克、3克、4克的砝码各一枚,能称出哪几种重量?各有几种可能方案?
如何解决这个问题呢?考虑构造母函数。
如果用x的指数表示称出的重量,则:
1个1克的砝码可以用函数1+x表示,
1个2克的砝码可以用函数1+x2表示,
1个3克的砝码可以用函数1+x3表示,
1个4克的砝码可以用函数1+x4表示
几种砝码的组合可以称重的情况,可以用以上几个函数的乘积表示:
(1+x)(1+x2)(1+x3)(1+x4)=(1+x+x2+x3)(1+x3+x4+x7)=1+x+x2+2x3+2x4+2x5+2x6+2x7+x8+x9+x10
从上面的函数知道:可称出从1克到10克,系数便是方案数。
例如右端有2x5 项,即称出5克的方案有2:5=3+2=4+1;同样,6=1+2+3=4+2;10=1+2+3+4。
故称出6克的方案有2,称出10克的方案有1
编程:
// Author by lwg
#include <iostream>
using namespace std;
const int lmax=10000;
int c1[lmax+1],c2[lmax+1];
int main(){
int n,i,j,k;
while (cin>>n){
for (i=0;i<=n;i++){
c1[i]=0;
c2[i]=0
}
for(i=0;i<=n;i++)c1[i]=1;
for(i=2;i<=n;i++){
for(j=0;j<=n;j++)
for (k=0;k+j<=n;k+=i)
c2[j+k]+=c1[j];
for (j=0;j<=n;j++){
c1[j]=c2[j];
c2[j]=0;
}
}
cout<<c1[n]<<endl;
}
return 0;
}
这里第一个式子(1+x^1+x^2+x^3+…+x^n)
第二个式子 (1+x^2+x^4+x^6+…+x^n)
首先,明确一点:c1[]数组存储原式(当前为式1)的系数c2[]存储原式每项去乘新式(现为式2)每项的系数。
然后以此类推先计算前面k-1个式子的乘积的系数数组,然后计算前k-1式与第k式的乘积。。。
然后明确:j表原多项式次数那么当j=1时,指式1当中x^1当中的1次。
k表示新多项式次数。i表示已经遍历到了第几个多项式。第二个多项式的幂增幅为i=2.
最重要的就是明确c2[j+k]+=c1[j];
它表示原式j次幂项*新式k次幂项得到新式j+k次幂项,也就是将原式j次项系数放到新式系数数组的第j+k位
然后,如上程序一直循环到遍历完原式,使其中每个x^之前的系数都与新式x^之前系数相乘(即程序中的+)
然后把当前新式当作原式,新式清0,继续直到遍历完所有式子,使他们都相乘。
得到的c1数组就是所有式子相乘之后的系数数组。
#include <iostream>
#include <iomanip>
#include <string>
using namespace std;
void main(){
int N;
cin>>N;
int c1[1000],c2[1000],words;
for(int i=0;i<N;i++){
for(int j=0;j<1000;j++)
c1[j]=c2[j] = 0;
c1[0] = 1;
for(int l=1;l<=26;l++){
cin>>words;
if(!words)continue;
for(int j=0;j<1000;j++)
for(int k=0;k<=words && k*l+j<=50;k++)
//用l*k表示该字幕的重
c2[j+l*k] += c1[j];
for(int j=0;j<1000;j++){
c1[j] = c2[j];
c2[j] = 0;
}
}
words = 0;
//l要从1开始计数,因为一个字幕也不取不能构成单词
for(int l=1;l<1000;l++)
words+=c1[l];
cout<<words<<endl;
}
}