算法的开章,递归是实现其他高级算法如深度优先、分治等的基础;
碰到一个题目就找它的重复性,重复性有最近的重复性(根据重复性怎么构造怎么分解-->分治、回溯等办法,本质就是递归),或者最优重复性(即动态规划)。
本质上就是找它的重复性。
找重复性以及分解问题,最后组合每个子问题的结果。
1. 分治 Divide & Conquer
先把一个大的问题剖析成一个个的子问题,子问题再一一的解决;
庖丁解牛,依次对子问题进行分析;
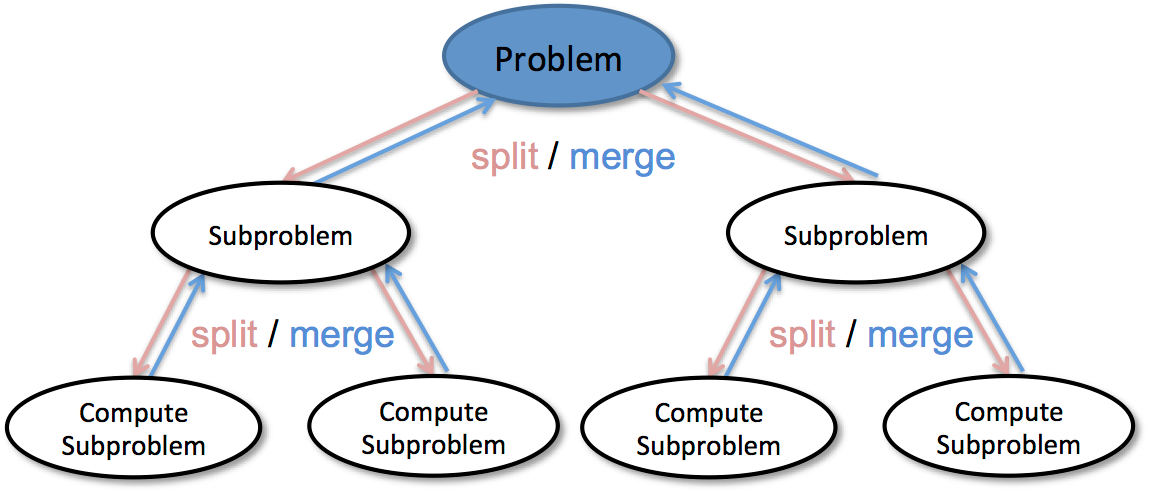
一个大问题分成小问题,小问题依次解决后再合并结果返回数据,有点像分布式系统中的mapReduce。
例子:给定一个字符串,把它的每个字符都变成大写;
可以写循环,或者递归

如上图做法的好处是可以并行计算,每个子问题是互不相关的,可以在多核CPU中跑。
分治可以解决的问题,它没有所谓的中间结果(重复计算),如果有大量重复计算如递归分治的效率并不高,这时可以有更适合的算法,比如动态规划、 把中间结果先保存下来下次直接使用。
分治的代码模板:分治一般是用递归来处理的

怎么拆分为子问题,怎么merge这些subresult,得到这些子结果怎么合并起来; 中间的这些子结果如何做质量控制和质量保证,下面的人给你个返回结果你咋知道他做的好还是坏。
专注本层,不要下探。
2. 回溯 Backtrackin
回溯法采用试错的思想,它尝试分步的去解决一个问题。在分步解决问题的过程 中,当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候,它将 取消上一步甚至是上几步的计算,再通过其它的可能的分步解答再次尝试寻找问 题的答案。
回溯法通常用最简单的递归方法来实现,在反复重复上述的步骤后可能出现两种情况:
- 找到一个可能存在的正确的答案;
- 在尝试了所有可能的分步方法后宣告该问题没有答案。
在最坏的情况下,回溯法会导致一次复杂度为指数时间的计算。
就是不断的在每一层进行试,经典应用是八皇后问题以及数独问题上,简单的比如括号的生成。归去来兮的感觉。
*回溯算法框架。解决一个回溯问题,实际上就是一个决策树的遍历过程。你只需要思考 3 个问题:
* 1、路径:也就是已经做出的选择。
* 2、选择列表:也就是你当前可以做的选择。
* 3、结束条件:也就是到达决策树底层,无法再做选择的条件。
* 回溯算法框架代码:
*
* result = []
* def backtrack(路径, 选择列表):
* if 满足结束条件:
* result.add(路径)
* return
*
* for 选择 in 选择列表:
* 做选择
* backtrack(路径, 选择列表) -- 递归
* 撤销选择
* 链接:https://leetcode-cn.com/problems/permutations/solution/hui-su-suan-fa-xiang-jie-by-labuladong-2/
* 来源:力扣(LeetCode)