1. 图的概念
图(Graph)另一种非线性表数据结构。
树中的元素称为节点,图中的元素叫作顶点(vertex)。图中的一个顶点可以与任意其他顶点建立连接关系。这种建立的关系叫作边(edge)。比如社交网络就是一种典型的图结构。
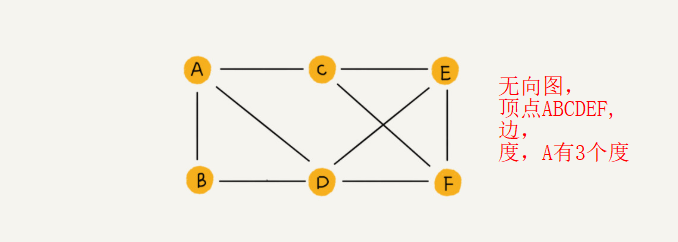
跟顶点相连接的边的条数叫作顶点的度(degree)。(如微信中 把每个用户看作一个顶点。如果两个用户之间互加好友,那就在两者之间建立一条边;其中,每个用户有多少个好友,对应到图中,就叫作顶点的度。 )
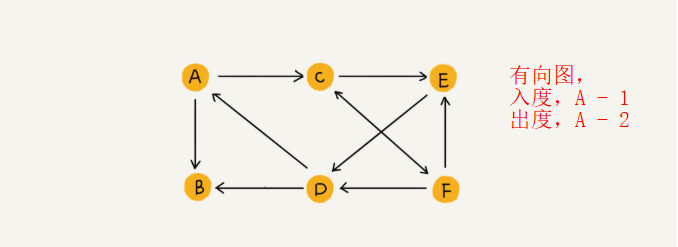
有方向的图叫作“有向图”。 (微博中可以单向关注,如果用户 A 关注了用户 B,我们就在图中画一条从 A 到 B 的带箭头的边,来表示边的方向。如果用户 A 和用户 B 互相关注了,那我们就画一条从 A 指向 B 的边,再画一条从 B 指向 A 的边)
以此类推,我们把边没有方向的图就叫作“无向图”。
无向图中有“度”这个概念,表示一个顶点有多少条边。在有向图中,把度分为入度(In-degree)和出度(Out-degree)。
顶点的入度,表示有多少条边指向这个顶点;顶点的出度,表示有多少条边是以这个顶点为起点指向其他顶点。 (微博的例子,入度就表示有多少粉丝,出度就表示关注了多少人。)
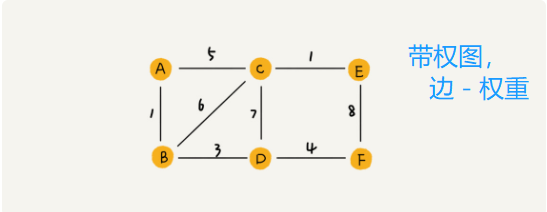
带权图(weighted graph)。在带权图中,每条边都有一个权重(weight),我们可以通过这个权重来表示 QQ 好友间的亲密度。 (QQ 不仅记录了用户之间的好友关系,还记录了两个用户之间的亲密度)
2. 图的存储
2.1 邻接矩阵(Adjacency Matrix)
图最直观的一种存储方法就是,邻接矩阵(Adjacency Matrix), 邻接矩阵的底层依赖一个二维数组。
对于无向图来说,如果顶点 i 与顶点 j 之间有边,我们就将 A[i][j] 和 A[j][i] 标记为 1;
对于有向图来说,如果顶点 i 到顶点 j 之间,有一条箭头从顶点 i 指向顶点 j 的边,那我们就将 A[i][j] 标记为 1。
同理,如果有一条箭头从顶点 j 指向顶点 i 的边,我们就将 A[j][i] 标记为 1。对于带权图,数组中就存储相应的权重。

邻接矩阵来表示一个图,虽然简单、直观,但是比较浪费存储空间。
对于无向图来说,如果 A[i][j] 等于 1,那 A[j][i] 也肯定等于 1。实际上,我们只需要存储一个就可以了。也就是说,无向图的二维数组中,如果我们将其用对角线划分为上下两部分,那我们只需要利用上面或者下面这样一半的空间就足够了,另外一半白白浪费掉了。
还有,如果我们存储的是稀疏图(Sparse Matrix),也就是说,顶点很多,但每个顶点的边并不多,那邻接矩阵的存储方法就更加浪费空间了。
优点:
首先,邻接矩阵的存储方式简单、直接,因为基于数组,所以在获取两个顶点的关系时,就非常高效。
其次,用邻接矩阵存储图的另外一个好处是方便计算。这是因为,用邻接矩阵的方式存储图,可以将很多图的运算转换成矩阵之间的运算。比如求解最短路径问题时会提到一个Floyd-Warshall 算法,就是利用矩阵循环相乘若干次得到结果。
2.2 邻接表(Adjacency List)
在图中,如果两个点相互连通,即通过其中一个顶点,可直接找到另一个顶点,则称它们互为邻接点。(邻接指的是图中顶点之间有边或者弧的存在。)
邻接表存储图的实现方式是,给图中的各个顶点独自建立一个链表,用节点存储该顶点,用链表中其他节点存储各自的临界点。
每个顶点对应一条链表,链表中存储的是与这个顶点相连接的其他顶点。
下图是一个有向图的邻接表存储方式,每个顶点对应的链表里面,存储的是指向的顶点。
对于无向图来说,也是类似的,不过,每个顶点的链表中存储的,是跟这个顶点有边相连的顶点

邻接矩阵 VS 邻接表
邻接矩阵存储起来比较浪费空间,但是使用起来比较节省时间。
相反,邻接表存储起来比较节省空间,但是使用起来就比较耗时间。(时间、空间复杂度互换的设计思想)
就像图中的例子,如果我们要确定,是否存在一条从顶点 2 到顶点 4 的边 ?
那我们就要遍历顶点 2 对应的那条链表,看链表中是否存在顶点 4。而且,我们前面也讲过,链表的存储方式对缓存不友好。所以,比起邻接矩阵的存储方式,在邻接表中查询两个顶点之间的关系就没那么高效了。
在基于链表法解决冲突的散列表中,如果链过长,为了提高查找效率,可以将链表换成其他更加高效的数据结构,比如平衡二叉查找树等。邻接表长得很像散列。所以,可以将邻接表同散列表一样进行“改进升级”。
可以将邻接表中的链表改成平衡二叉查找树。实际开发中,我们可以选择用红黑树。这样就可以更加快速地查找两个顶点之间是否存在边了。当然,这里的二叉查找树可以换成其他动态数据结构,比如跳表、散列表等。除此之外,我们还可以将链表改成有序动态数组,可以通过二分查找的方法来快速定位两个顶点之间否是存在边。
3. 应用
在微博中,两个人可以互相关注;在微信中,两个人可以互加好友。 微博、微信是两种“图”,前者是有向图(入度和出度概念),后者是无向图(度的概念)。
微博,微博允许单向关注,微博的入度就表示有多少粉丝,出度就表示关注了多少人。
QQ 不仅记录了用户之间的好友关系,还记录了两个用户之间的亲密度 --- 带权图(weighted graph)。在带权图中,每条边都有一个权重(weight),我们可以通过这个权重来表示 QQ 好友间的亲密度。