1. BF和 RK算法
2. BM(Boyer-Moore)算法
对于工业级的软件开发来说,我们希望算法尽可能的高效,并且在极端情况下,性能也不要退化 的太严重。那么,对于查找功能是重要功能的软件来说,比如一些文本编辑器,它们的查找功能 都是用哪种算法
来实现的呢? 有没有比 BF 算法和 RK 算法更加高效的字符串匹配算法呢? 即 BM(Boyer-Moore)算法。它是一种非常高效的字符串匹配算法,有实验统计,它的性能是著名的KMP 算法的 3 到 4 倍。
BM 算法的核心思想
模式串和主串的匹配过程,看作模式串在主串中不停地往后滑动。当遇到不匹配的字符时,BF 算法和 RK 算法的做法是,模式串往后滑动一位,然后从模式串的第一个字符开始重新匹配。
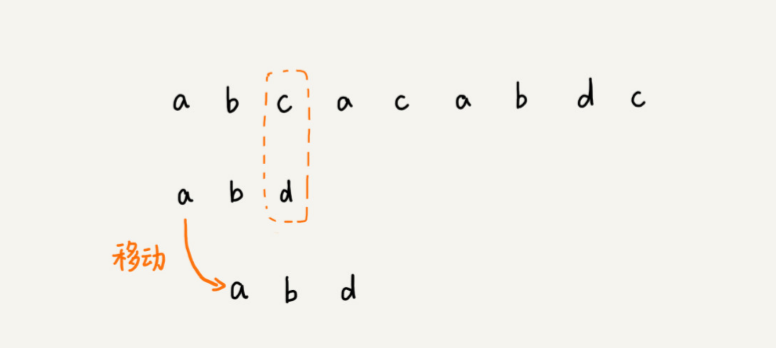
主串中的 c,在模式串中是不存在的,所以,模式串向后滑动的时候,只要 c 与模式串有重合,肯定无法匹配。所以,可以一次性把模式串往后多滑动几位,把模式串移动 到 c 的后面。
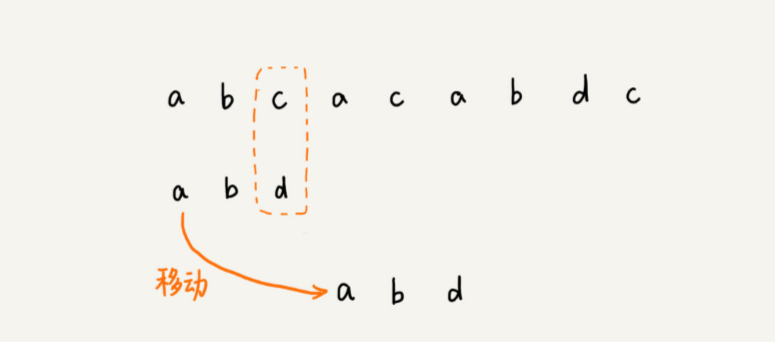
由现象找规律,当遇到不匹配的字符时,有什么固定的规律,可以将模式串往后多滑动几位呢?这样一次性往后滑动好几位,那匹配的效率岂不是就提高了?
BM 算法,本质上其实就是在寻找这种规律。借助这种规律,在模式串与主串匹配的过程中,当模式串和主串某个字符不匹配的时候,能够跳过一些肯定不会匹配的情况,将模式串往后多滑动几位。
BM 算法原理分析
BM 算法包含两部分,分别是坏字符规则(bad character rule)和好后缀规则(good suffix shift)
1. 坏字符规则
之前在匹配的过程中,都是按模式串的下标从小到大的顺序,依次与主串中 的字符进行匹配的。这种匹配顺序比较符合我们的思维习惯,而 BM 算法的匹配顺序比较特 别,它是按照模式串下标从大到小的顺序,倒着匹配的。
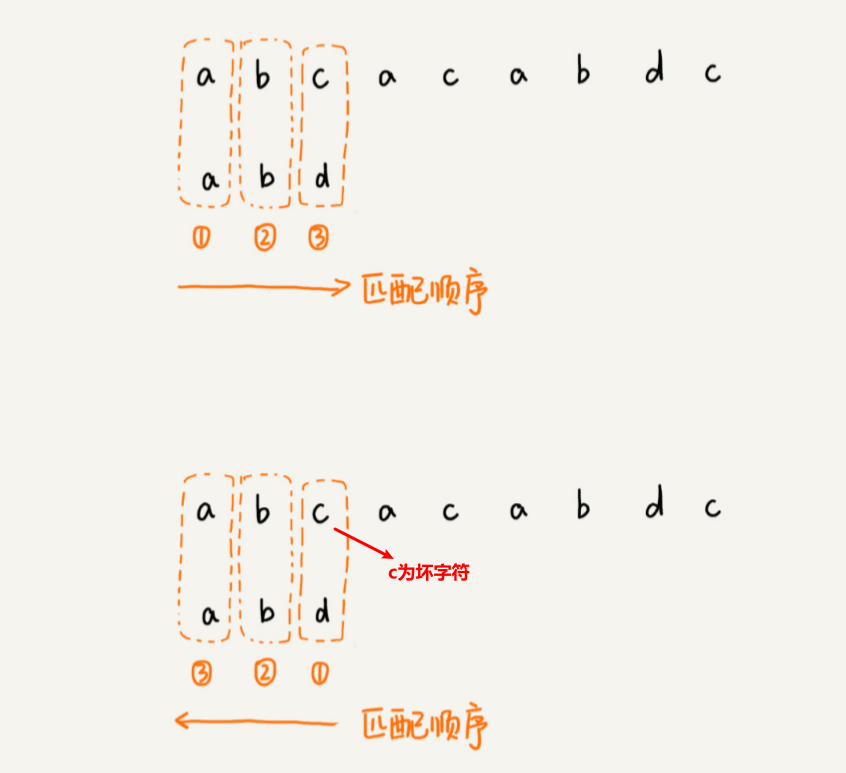
从模式串的末尾往前倒着匹配,当发现某个字符没法匹配的时候。把这个没有匹配的字符叫作坏字符(主串中的字符)。
拿坏字符 c 在模式串中查找,发现模式串中并不存在这个字符,也就是说,字符c 与模式串中的任何字符都不可能匹配。这个时候,我们可以将模式串直接往后滑动三位,将模式串滑动到c 后面的位置,再从模式串的末尾字符开始比较。

发现,模式串中后一个字符 d,还是无法跟主串中的 a 匹配,这个时候,还能将模式串往后滑动三位吗?答案是不行的。因为这个时候,坏字符 a 在模式串中是存在的, 模式串中下标是 0 的位置也是字符 a。这种情况下,我们可以将模式串往后滑动两位,让两个 a 上下对齐,然后再从模式串的末尾字符开始,重新匹配。
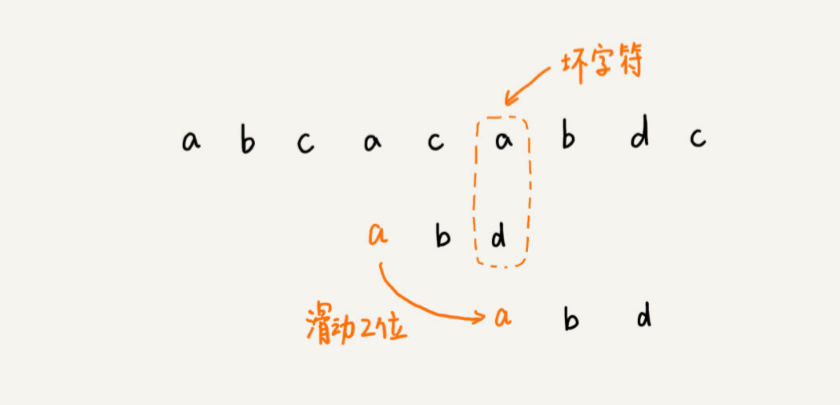
第一次不匹配的时候,滑动了三位,第二次不匹配的时候,将模式串后移两位,那具体滑动多少位,到底有没有规律呢?
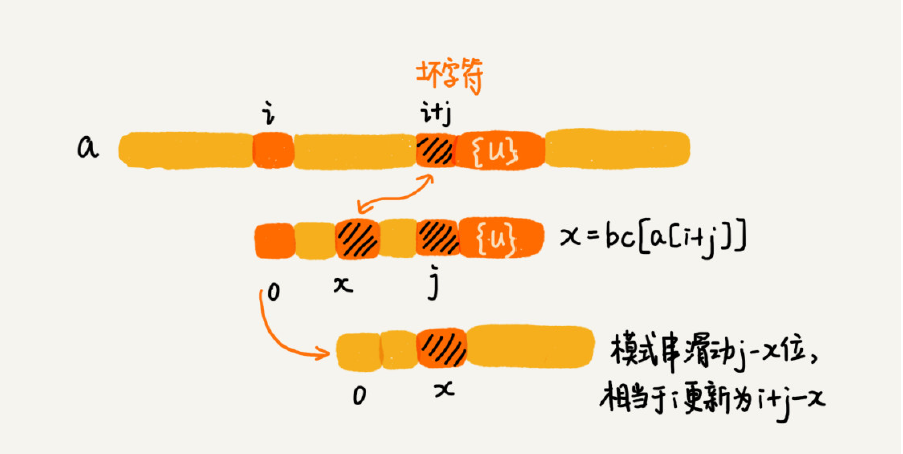
当发生不匹配的时候,把坏字符对应的模式串中的字符下标记作 si。如果坏字符在模式串中存在,我们把这个坏字符在模式串中的下标记作 xi。
如果不存在,我们把 xi 记作 -1。那模式串 往后移动的位数就等于 si - xi。(注意,这里说的下标,都是字符在模式串的下标)。
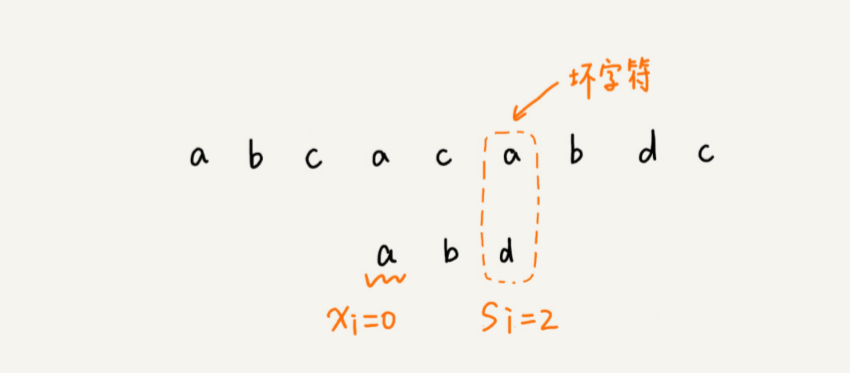
如果坏字符在模式串里多处出现,那我们在计算 xi 的时候,选择靠后的那个,因为这样不会让模式串滑动过多,导致本来可能匹配的情况被滑动略过。
利用坏字符规则,BM 算法在好情况下的时间复杂度非常低,是 O(n/m)。比如,主串是 aaabaaabaaabaaab,模式串是 aaaa。每次比对,模式串都可以直接后移四位,所以,匹配具 有类似特点的模式串和主串的时候,BM 算法非常高效。
不过,单纯使用坏字符规则还是不够的。因为根据 si-xi 计算出来的移动位数,有可能是负数, 比如主串是 aaaaaaaaaaaaaaaa,模式串是 baaa。不但不会向后滑动模式串,还有可能倒退。 所以,BM 算法还需要用到“好后缀规则”。
2. 好后缀规则
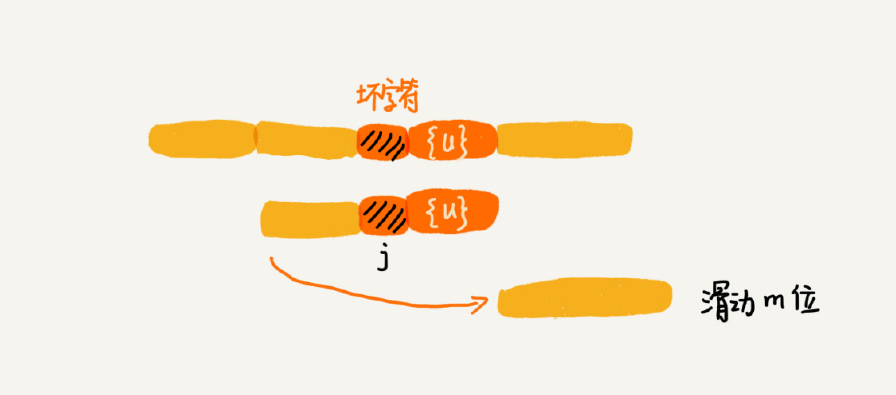
好后缀规则实际上跟坏字符规则的思路很类似。当模式串滑动到图中位置的时候,模式串和主串有 2 个字符是匹配的,倒数第 3 个字符发生了不匹配的情况。
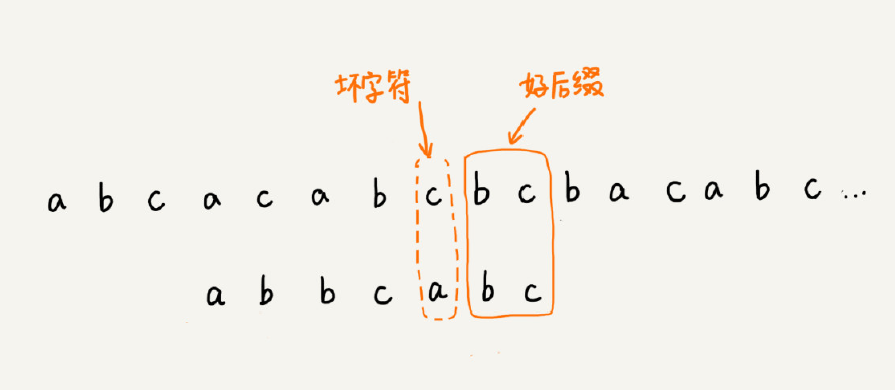
把已经匹配的 bc 叫作好后缀,记作{u}。我们拿它在模式串中查找,如果找到了另一个跟{u}相匹配的子串{u*},就将模式串滑动到子串{u*}与主串中{u}对齐的位置。
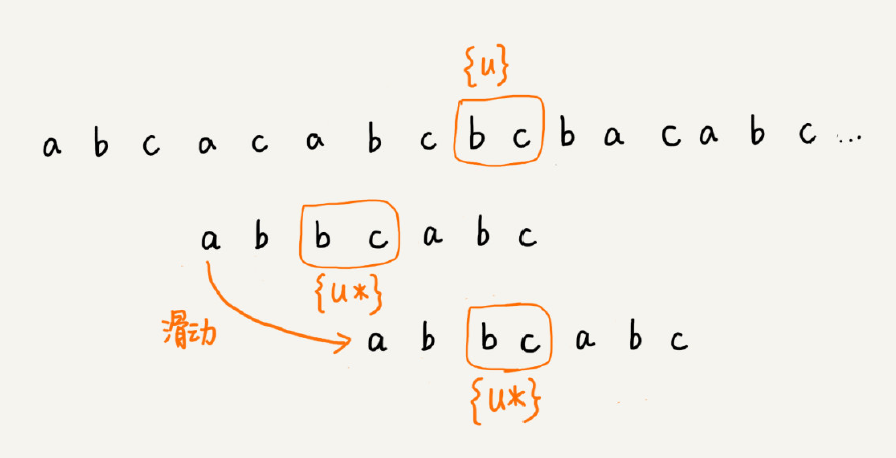
如果在模式串中找不到另一个等于{u}的子串,就直接将模式串,滑动到主串中{u}的后面,因为之前的任何一次往后滑动,都没有匹配主串中{u}的情况。
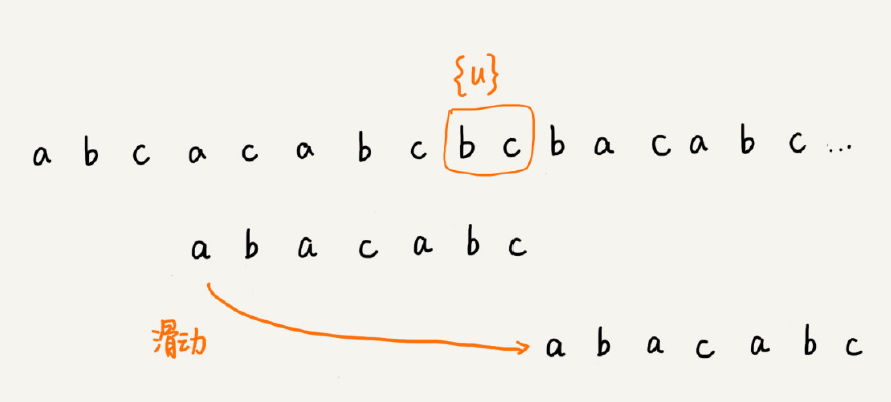
当模式串中不存在等于{u}的子串时,直接将模式串滑动到主串{u}的后面。这样做是否有点太过头呢?看下面这个例子。这里面 bc 是好后缀,尽管在模式串中没有另外一个
相匹配的子串{u*},但是如果我们将模式串移动到好后缀的后面,如图所示,那就会错过模式串和主串可以匹配的情况。
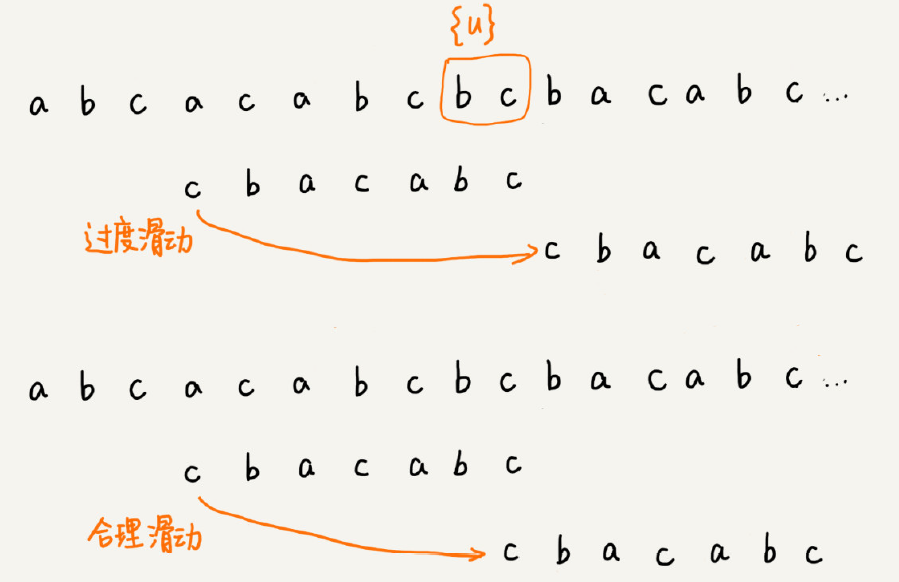
如果好后缀在模式串中不存在可匹配的子串,那在我们一步一步往后滑动模式串的过程中,只要主串中的{u}与模式串有重合,那肯定就无法完全匹配。但是当模式串滑动到前缀与主串中{u}的后缀有部分重合的时候,并且重合的部分相等的时候,就有可能会存在完全匹配的情况。
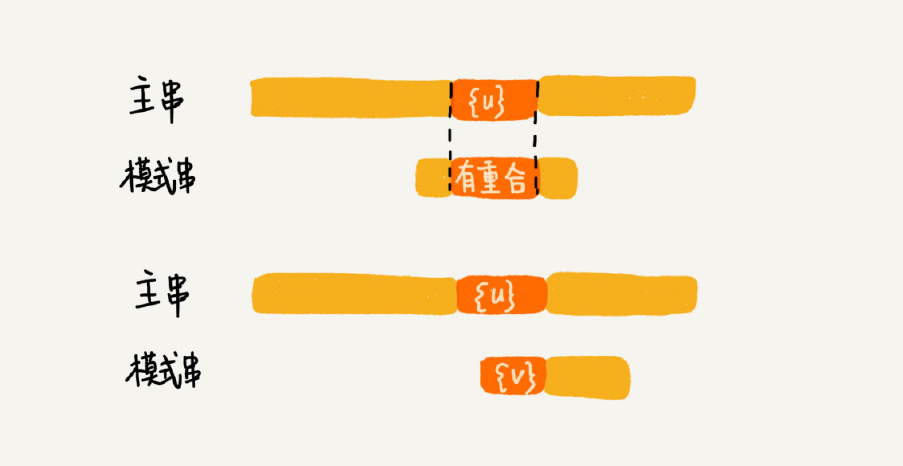
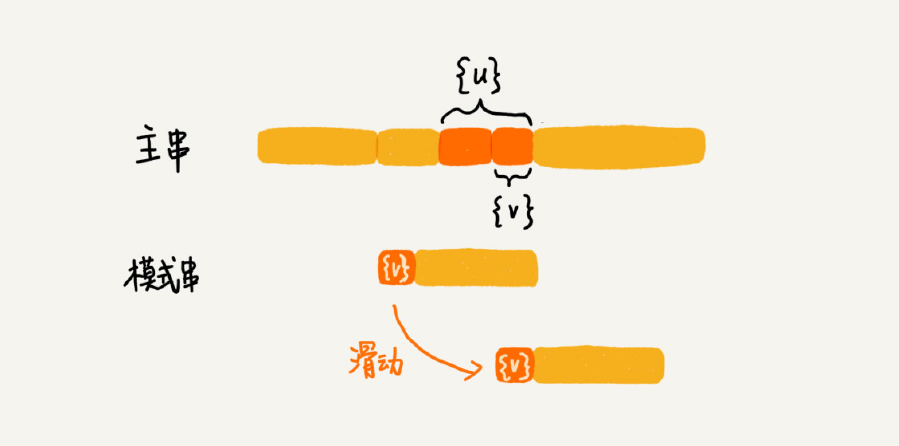
针对这种情况,我们不仅要看好后缀在模式串中,是否有另一个匹配的子串,我们还要考察好后缀的后缀子串,是否存在跟模式串的前缀子串匹配的。
所谓某个字符串 s 的后缀子串,就是最后一个字符跟 s 对齐的子串,比如 abc 的后缀子串就包括 c, bc。所谓前缀子串,就是起始字符跟 s 对齐的子串,比如 abc 的前缀子串有 a,ab。我们从好后缀的后缀子串中,找一个最长的并且能跟模式串的前缀子串匹配的,假设是{v},然后将模式串滑动到如图所示的位置。
当模式串和主串中的某个字符不匹配的时候,如何选择用好后缀规则还是坏字符规则,来计算模式串往后滑动的位数?
我们可以分别计算好后缀和坏字符往后滑动的位数,然后取两个数中最大的,作为模式串往后滑动的位数。这种处理方法还可以避免我们前面提到的,根据坏字符规则,计算得到的往后滑动的位数,有可能是负数的情况。
BM 算法代码实现

/** * BM 算法 */ public class BM { private static final int SIZE = 256; // 全局变量或成员变量 /** * 将模式串中的每个字符及其下标都存到散列表中。这样就可以快速找到坏字符在模式串的位置下标了 * @param b 模式串 * @param m 模式串的长度 * @param bc 散列表, 只实现一种简单的情况, 假设字符串的字符集不是很大, 每个字符长度是1字节,用大小为256的数组来记录每个字符在模式串中出现的位置。 * 数组的下标对应字符的 ASCII 码值, 数组中存储这个字符在模式串中出现的位置. * 散列表下标为 模式串的字符所对应的ASCII数值, * 散列表的value值为 模式串的下标; */ private void generateBC(char[] b, int m, int[] bc) { for (int i = 0; i < SIZE; i++) { bc[i] = -1; // 初始化 bc即散列表 } for (int i = 0; i < m; i++) { int ascii = (int) b[i]; // 计算 b[i] 的 ASCII 值 bc[ascii] = i; } } /** * 暴力解法, 框架的搭建 * @param a 主串 * @param n 主串的长度 * @param b 模式串 * @param m 模式串的长度 * @return */ public int bm(char[] a, int n, char[] b, int m) { int[] bc = new int[SIZE]; generateBC(b, m, bc); //i, j,双指针(头指针和 尾指针) int i = 0; while (i <= n - m) { int j; for (j = m - 1; j >= 0; j--) { if (a[i+j] != b[j]) break; } if (j < 0) { return i; } i = i + (j - bc[(int) a[i+j]]); //往后移动i 位 } return -1; } /** * suffix 数组和 prefix 数组的计算过程 * @param b 模式串 * @param m 模式串的长度 * @param suffix suffix 数组的下标k 表示后缀子串的长度, 下标对应的数组值存储的是在模式串中跟好后缀{u}相匹配的子串{u*}的起始下标值 * @param prefix prefix数组来记录模式串的后缀子串 是否能匹配模式串的前缀子串 */ private void generateGS(char[] b, int m, int[] suffix, boolean[] prefix) { for (int i = 0; i < m; i++) { suffix[i] = -1; prefix[i] = false; } for (int i = 0; i < m - 1; i++) { int j = i; int k = 0; while (j >= 0 && b[j] == b[m-1-k]) { j--; k++; suffix[k] = j+1; } if (j == -1) prefix[k] = true; } } // a,b 表示主串和模式串;n,m 表示主串和模式串的长度。 public int bm2(char[] a, int n, char[] b, int m) { int[] bc = new int[SIZE]; // 记录模式串中每个字符最后出现的位置 generateBC(b, m, bc); // 构建坏字符哈希表 int[] suffix = new int[m]; boolean[] prefix = new boolean[m]; generateGS(b, m, suffix, prefix); int i = 0; // j 表示主串与模式串匹配的第一个字符 while (i <= n - m) { int j; for (j = m - 1; j >= 0; --j) { // 模式串从后往前匹配 if (a[i+j] != b[j]) break; // 坏字符对应模式串中的下标是 j } if (j < 0) { return i; // 匹配成功,返回主串与模式串第一个匹配的字符的位置 } int x = j - bc[(int)a[i+j]]; int y = 0; if (j < m-1) { // 如果有好后缀的话 y = moveByGS(j, m, suffix, prefix); } i = i + Math.max(x, y); } return -1; } private int moveByGS(int j, int m, int[] suffix, boolean[] prefix) { int k = m - 1 - j; // 好后缀长度 if (suffix[k] != -1) return j - suffix[k] +1; for (int r = j+2; r <= m-1; ++r) { if (prefix[m-r] == true) { return r; } } return m; } }
“坏字符规则”,当遇到坏字符时,要计算往后移动的位数 si-xi,其中 xi 的计算是重点,我们如何求得 xi 呢?或者说,如何查找坏字符在模式串中出现的位置呢?
如果我们拿坏字符,在模式串中顺序遍历查找,这样就会比较低效,势必影响这个算法的性能。有没有更加高效的方式呢?
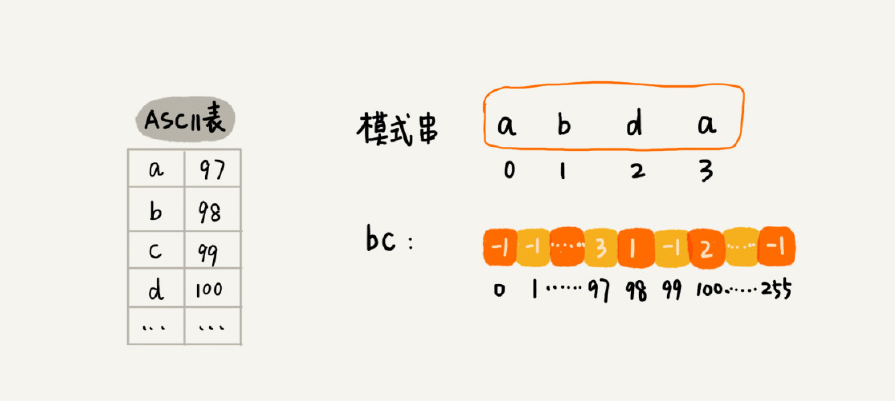
散列表,可以将模式串中的每个字符及其下标都存到散列表中。这样就可以快速找到坏字符在模式串的位置下标了。
假设字符串的字符集不是很大,每个字符长度是 1 字节,用大小为 256 的数组,来记录每个字符在模式串中出现的位置。数组的下标对应字符的 ASCII 码值,数组中存储这个字符在模式串中出现的位置。
如何实现好后缀规则。它的实现要比坏字符规则复杂一些。好后缀的处理规则中最核心的内容:
- 在模式串中,查找跟好后缀匹配的另一个子串;
- 在好后缀的后缀子串中,查找最长的、能跟模式串前缀子串匹配的后缀子串;
在不考虑效率的情况下,这两个操作都可以用很“暴力”的匹配查找方式解决。但是,如果想要BM 算法的效率很高,这部分就不能太低效。如何来做?
因为好后缀也是模式串本身的后缀子串,所以,我们可以在模式串和主串正式匹配之前,通过预处理模式串,预先计算好模式串的每个后缀子串,对应的另一个可匹配子串的位置。这个预处理过程比较有技巧,很不好懂。
我们先来看,如何表示模式串中不同的后缀子串呢?因为后缀子串的最后一个字符的位置是固定的,下标为 m-1,只需要记录长度就可以了。通过长度,可以确定一个唯一的后缀子串。
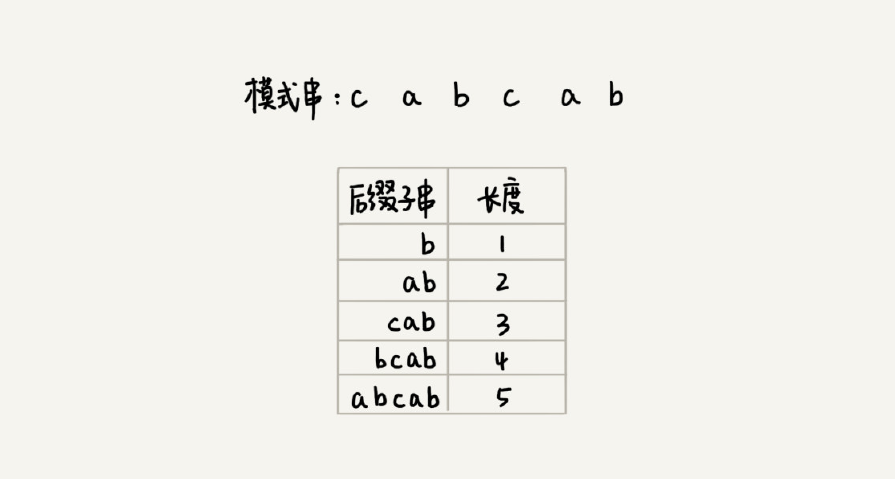
引入最关键的变量 suffix 数组。suffix 数组的下标 k,表示后缀子串的长度,下标对应的数组值存储的是,在模式串中跟好后缀{u}相匹配的子串{u*}的起始下标值。

但是,如果模式串中有多个(大于 1 个)子串跟后缀子串{u}匹配,那 suffix 数组中该存储哪一个子串的起始位置呢?为了避免模式串往后滑动得过头了,肯定要存储模式串中最靠后的那个子串的起始位置,也就是下标最大的那个子串的起始位置。不过,这样处理就足够了吗?
实际上,仅仅是选最靠后的子串片段来存储是不够的。好后缀规则:我们不仅要在模式串中,查找跟好后缀匹配的另一个子串,还要在好后缀的后缀子串中,查找最长的能跟模式串前缀子串匹配的后缀子串。
如果我们只记录刚刚定义的 suffix,实际上,只能处理规则的前半部分,也就是,在模式串中,查找跟好后缀匹配的另一个子串。所以,除了 suffix 数组之外,我们还需要另外一个 boolean类型的 prefix 数组,来记录模式串的后缀子串是否能匹配模式串的前缀子串。

如何来计算并填充这两个数组的值?这个计算过程非常巧妙。
我们拿下标从 0 到 i 的子串(i 可以是 0 到 m-2)与整个模式串,求公共后缀子串。如果公共后缀子串的长度是 k,那我们就记录 suffix[k]=j(j 表示公共后缀子串的起始下标)。如果 j 等于0,也就是说,公共后缀子串也是模式串的前缀子串,我们就记录 prefix[k]=true。

有了这两个数组之后,我们现在来看,在模式串跟主串匹配的过程中,遇到不能匹配的字符时,如何根据好后缀规则,计算模式串往后滑动的位数?
假设好后缀的长度是 k。先拿好后缀,在 suffix 数组中查找其匹配的子串。如果 suffix[k]不等于 -1(-1 表示不存在匹配的子串),那我们就将模式串往后移动 j-suffix[k]+1 位(j 表示坏字符对应的模式串中的字符下标)。如果 suffix[k] 等于 -1,表示模式串中不存在另一个跟好后缀匹配的子串片段。我们可以用下面这条规则来处理。
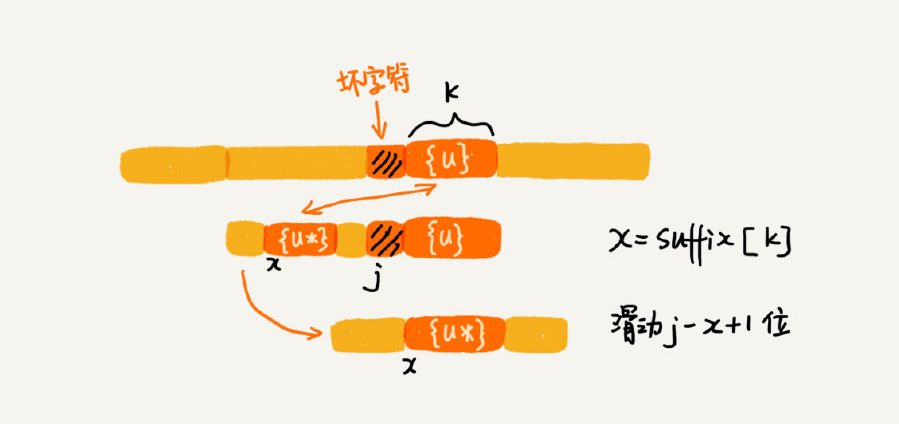
好后缀的后缀子串 b[r, m-1](其中,r 取值从 j+2 到 m-1)的长度 k=m-r,如果 prefix[k] 等于 true,表示长度为 k 的后缀子串,有可匹配的前缀子串,这样我们可以把模式串后移 r 位。
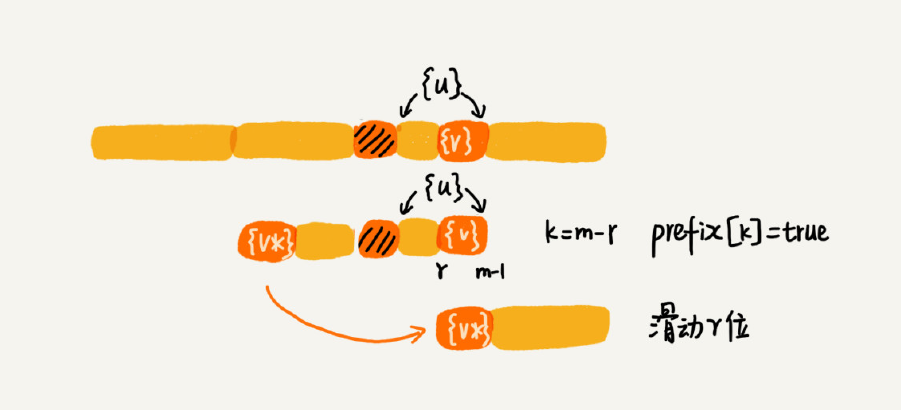
如果两条规则都没有找到可以匹配好后缀及其后缀子串的子串,我们就将整个模式串后移 m位。
BM 算法的性能分析及优化
BM 算法的内存消耗。整个算法用到了额外的 3 个数组,其中 bc 数组的大小跟字符集大小有关,suffix 数组和 prefix 数组的大小跟模式串长度 m 有关。
如果我们处理字符集很大的字符串匹配问题,bc 数组对内存的消耗就会比较多。因为好后缀和坏字符规则是独立的,如果我们运行的环境对内存要求苛刻,可以只使用好后缀规则,不使用坏字符规则,这样就可以避免 bc 数组过多的内存消耗。不过,单纯使用好后缀规则的 BM 算法效率就会下降一些了。
对于执行效率来说,可以先从时间复杂度的角度来分析。
实际上,前面讲的 BM 算法是个初级版本。为了让你能更容易理解,有些复杂的优化没讲。基于我目前讲的这个版本,在极端情况下,预处理计算 suffix 数组、prefix 数组的性能会比较差。
比如模式串是 aaaaaaa 这种包含很多重复的字符的模式串,预处理的时间复杂度就是O(m^2)。当然,大部分情况下,时间复杂度不会这么差。关于如何优化这种极端情况下的时间复杂度退化,如果感兴趣,你可以自己研究一下。
实际上,BM 算法的时间复杂度分析起来是非常复杂,这篇论文“A new proof of the linearityof the Boyer-Moore string searching algorithm”证明了在最坏情况下,BM 算法的比较次数上限是 5n。这篇论文“Tight bounds on the complexity of the Boyer-Moore string matching algorithm” 证明了在最坏情况下,BM 算法的比较次数上限是 3n
3. KMP 算法
Boyer-Moore 算法:https://www.ruanyifeng.com/blog/ 2013/05/boyer-moore_string_search_algorithm.html
Sunday 算法:https://blog.csdn.net/u012505432/article/ details/52210975
BM 算法,是工程中非常常用的一种高效字符串匹配算法。它是高效、常用的字符串匹配算法。不过,在所有的字符串匹配算法里,知名的非 KMP算法莫属。提到字符串匹配,首先想到的就是 KMP 算法。
在实际的开发中,几乎不大可能自己亲手实现一个 KMP算法。但是,可以学这个算法的思想,开拓眼界、锻炼下逻辑思维。
KMP 算法基本原理
KMP 算法是根据三位作者(D.E.Knuth,J.H.Morris 和 V.R.Pratt)的名字来命名的,算法的全称是 Knuth Morris Pratt 算法,简称为 KMP 算法。
KMP 算法的核心思想,跟BM 算法非常相近。
假设主串是a,模式串是b。在模式串与主串匹配的过程中,当遇到不可匹配的字符时,我们希望找到一些规律,可以将模式串往后多滑动几位,跳过那些肯定不会匹配的情况。
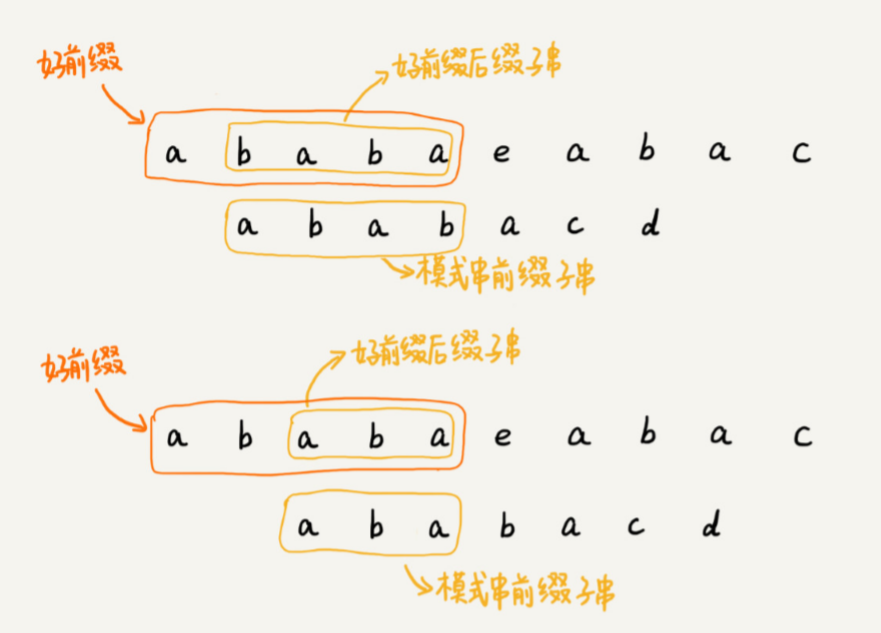
BM 算法中好后缀和坏字符吗?类比一下,在模式串和主串匹配的过程中,把不能匹配的那个字符仍然叫作坏字符,把已经匹配的那段字符串叫作好前缀。

当遇到坏字符的时候,就要把模式串往后滑动,在滑动的过程中,只要模式串和好前缀有上下重合,前面几个字符的比较,就相当于拿好前缀的后缀子串,跟模式串的前缀子串在比较。这个比较的过程能否更高效了呢?可以不用一个字符一个字符地比较了吗?
KMP算法就是在试图寻找一种规律:
在模式串和主串匹配的过程中,当遇到坏字符后,对于已经比对过的好前缀,能否找到一种规律,将模式串一次性滑动很多位?
只需要拿好前缀本身,在它的后缀子串中,查找长的那个可以跟好前缀的前缀子串匹配的。假设长的可匹配的那部分前缀子串是{v},长度是k。我们把模式串一次性往后滑动 j-k 位,相当于,每次遇到坏字符的时候,我们就把j更新为k,i不变,然后继续比较。

为表述方便,把好前缀的所有后缀子串中,最长的可匹配前缀子串的那个后缀子串,叫作最长可匹配后缀子串;
对应的前缀子串,叫作最长可匹配前缀子串。

如何来求好前缀的最长可匹配前缀和后缀子串呢?这个问题其实不涉及主串,只需要通过模式串本身就能求解。所以,能不能事先预处理计算好,在模式串和主串匹配的过程中,直接拿过来就用呢?
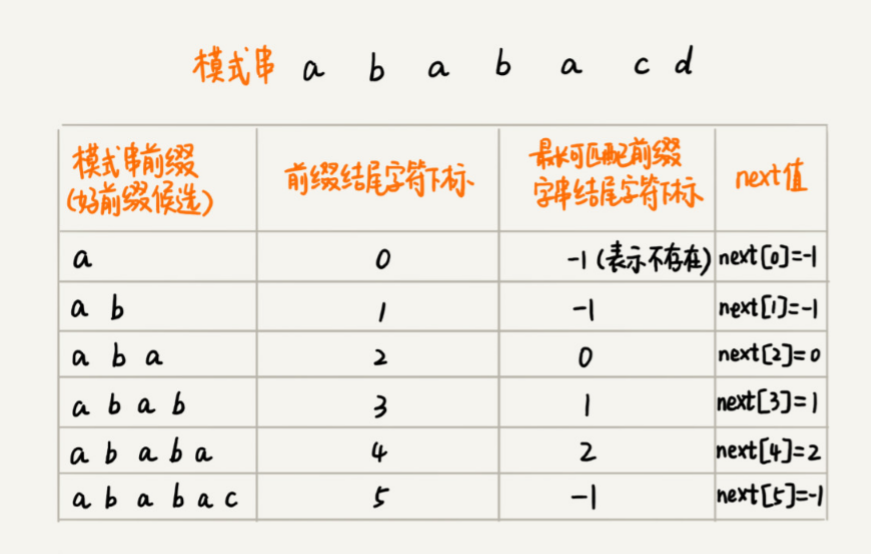
类似BM算法中的bc、suffix、prefix数组,KMP算法也可以提前构建一个数组,用来存储模式串中每个前缀(这些前缀都有可能是好前缀)的最长可匹配前缀子串的结尾字符下标。把这个数组定义为next 数组,也叫失效函数(failure function)。
数组的下标是每个前缀结尾字符下标,数组的值是这个前缀的长可以匹配前缀子串的结尾字符下标,如下图所示:
失效函数next数组计算方法
最复杂的部分,next数组是如何计算出来的?
当然,可以用非常笨的方法,比如要计算下面这个模式串 b 的 next[4],我们就把 b[0, 4] 的所有后缀子串,从长到短找出来,依次看看,是否能跟模式串的前缀子串匹配。很显然,这个方法也可以计算得到next数组,但是效率非常低。有没有更加高效的方法呢?

这里的处理非常有技巧,类似于动态规划。
按照下标从小到大,依次计算next数组的值。当我们要计算 next[i]的时候,前面的 next[0],next[1],……,next[i-1] 应该已经计算出来了。利用已经计算出来的next值,是否可以快速推导出 next[i]的值呢?
如果next[i-1]=k-1,也就是说,子串 b[0, k-1]是 b[0, i-1]的长可匹配前缀子串。如果子串 b[0, k-1] 的下一个字符 b[k],与 b[0, i-1] 的下一个字符 b[i] 匹配,那子串 b[0, k] 就是 b[0, i] 的长可匹配前缀子串。所以,next[i] 等于 k。但是,如果 b[0, k-1] 的下一字符 b[k] 跟 b[0, i-1] 的下一个字符 b[i] 不相等呢?这个时候就不能简单地通过 next[i-1] 得到 next[i] 了。这个时候怎么办呢?
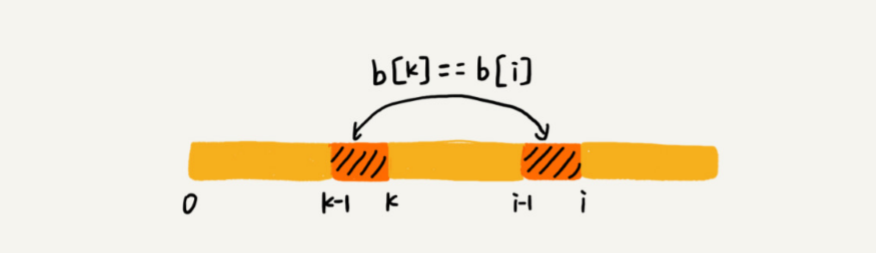
假设 b[0, i]的长可匹配后缀子串是 b[r, i]。如果把后一个字符去掉,那 b[r, i-1] 肯定是 b[0, i-1] 的可匹配后缀子串,但不一定是长可匹配后缀子串。所以,既然 b[0, i-1] 长可匹配后缀子串对应的模式串的前缀子串的下一个字符并不等于 b[i],那么我们就可以考察 b[0, i-1] 的次长可匹配后缀子串 b[x, i-1] 对应的可匹配前缀子串 b[0, i-1-x] 的下一个字符 b[ix] 是否等于 b[i]。如果等于,那 b[x, i] 就是 b[0, i] 的长可匹配后缀子串。
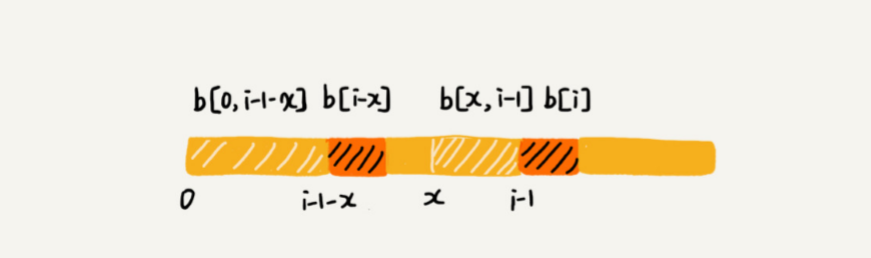
如何求得 b[0, i-1] 的次长可匹配后缀子串呢?次长可匹配后缀子串肯定被包含在长可 匹配后缀子串中,而长可匹配后缀子串又对应长可匹配前缀子串 b[0, y]。于是,查找 b[0, i-1] 的次长可匹配后缀子串,这个问题就变成,查找 b[0, y] 的长匹配后缀子串的问题了。

按照这个思路,我们可以考察完所有的b[0, i-1] 的可匹配后缀子串 b[y, i-1],直到找到一个可匹配的后缀子串,它对应的前缀子串的下一个字符等于 b[i],那这个 b[y, i] 就是 b[0, i] 的最长可匹配后缀子串
代码如下:

/** * @param a 主串 * @param n 主串长度 * @param b 模式串 * @param m 模式串的长度 * @return 匹配后的主串起始下标 */ public static int kmp(char[] a, int n, char[] b, int m) { int[] next = getNexts(b, m); int j = 0; for (int i = 0; i < n; i++) { while (j > 0 && a[i] != b[j]) { // 一直找到 a[i] 和 b[j] j = next[j - 1] + 1; } if (a[i] == b[j]) { j++; } if (j == m) { // 找到匹配模式串的了 return i - m + 1; } } return -1; } /** * next数组,失效函数 * 按照下标 i 从小到大,依次计算 next[i],并且 next[i] 的计算通过前面已经计算出来的 next[0],next[1],……,next[i-1]来推导 * @param b 表示模式串 * @param m 表示模式串的长度 * @return next数组也叫失效函数(failure function),用来存储模式串中每个前缀(这些前缀都有可能是好前缀)的最长可匹配前缀子串的结尾字符下标 * 数组的下标是每个前缀结尾字符下标, 数组的值是这个前缀的最长可以匹配前缀子串的结尾字符下标 */ private static int[] getNexts(char[] b, int m) { int[] next = new int[m]; next[0] = -1; int k = -1; for (int i = 1; i < m; i++) { while (k != -1 && b[k + 1] != b[i]) { k = next[k]; } if (b[k + 1] == b[i]) { k++; } next[i] = k; } return next; }
KMP算法复杂度分析
空间复杂度很容易分析,KMP算法只需要一个额外的next数组,数组的大小跟模式串相同。所以空间复杂度是 O(m),m 表示模式串的长度。
KMP算法包含两部分,第一部分是构建next数组,第二部分才是借助next数组匹配。
第一部分的时间复杂度。
计算next数组的代码中,第一层 for 循环中 i 从 1 到 m-1,也就是说,内部的代码被执行了 m-1 次。for 循环内部代码有一个 while 循环,如果我们能知道每次 for 循环、while 循环平均
执行的次数,假设是k,那时间复杂度就是O(k*m)。但是,while循环执行的次数不怎么好统 计,所以我们放弃这种分析方法。
我们可以找一些参照变量,i 和 k。i 从 1 开始一直增加到 m,而 k 并不是每次 for 循环都会增 加,所以,k 累积增加的值肯定小于 m。而 while 循环里 k=next[k],实际上是在减小 k 的 值,k 累积都没有增加超过 m,所以 while 循环里面 k=next[k] 总的执行次数也不可能超过 m。因此,next 数组计算的时间复杂度是 O(m)。
第二部分的时间复杂度。分析的方法是类似的
i 从 0 循环增长到 n-1,j 的增长量不可能超过 i,所以肯定小于 n。而 while 循环中的那条语句 j=next[j-1]+1,不会让 j 增长的,那有没有可能让 j 不变呢?也没有可能。因为 next[j-1] 的值 肯定小于 j-1,所以 while 循环中的这条语句实际上也是在让 j 的值减少。而 j 总共增长的量都 不会超过 n,那减少的量也不可能超过 n,所以 while 循环中的这条语句总的执行次数也不会超 过 n,所以这部分的时间复杂度是 O(n)。
所以,综合两部分的时间复杂度,KMP 算法的时间复杂度就是 O(m+n)。
KMP算法和BM算法的本质非常类似,都是根据规律在遇到坏字符的时候,把模式串往后多滑动几位。
BM算法有两个规则,坏字符和好后缀。KMP算法借鉴BM算法的思想,可以总结成好前缀规则。这里难懂的就是next数组的计算。如果用笨的方法来计算,确实不难,但是效率会比较低。所以讲了一种类似动态
规划的方法,按照下标i从小到大,依次计算next[i],并且 next[i]的计算通过前面已经计算出来的 next[0],next[1],……,next[i-1] 来推导。
KMP算法的时间复杂度是 O(n+m),不过它的分析过程稍微需要一点技巧,不那么直观,只要看懂就好了,并不需要掌握,在我们平常的开发中,很少会有这么难分析的代码。
