一、堆排序原理
1、什么是堆?
采用树形结构‘实现优先队列的一种有效技术称为堆。堆就是节点里存储数据的完全二叉树。堆包括大根堆和小根堆:
- 大顶堆 一颗完全二叉树,满足任一节点都比其孩子节点大,在堆排序算法中用于升序排列。
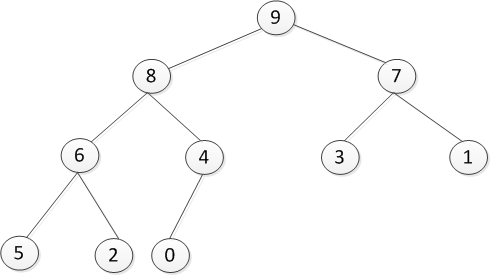
- 小顶堆 一颗完全二叉树,满足任一节点都比其孩子节点小,在堆排序算法中用于降序排列。
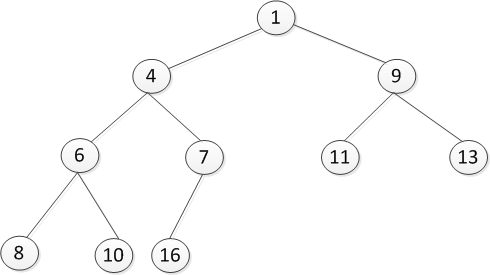
2、堆向下调整性质

可以看到,如果出现上图这种情况,根节点是4不符合大顶堆,但是其他节点符合,可以通过向下调整,将12放到4的位置,然后4放到12的位置,但是明显是不可行的,于是在6和9中选取9放到以前12的位置,于是出现下面的结果:

二、堆排序
1、算法步骤
- 建立堆
- 得到堆顶元素为最大元素
- 去掉堆顶,将堆最后一个元素放到堆顶,此时可通过一次调整重新使堆有序
- 堆顶元素为第二大元素
- 重复步骤三,直到堆为空
2、实现
def sift(li, start, last): temp = li[start] #表示每一棵树顶部的元素 i = start j = 2 * i + 1 #表示i节点左侧孩子的下标位置 while j <= last: # 退出循环条件:当前位置是叶子节点,j的位置超过了last if j + 1 <= last and li[j + 1] > li[j]: j = j + 1 # 如果右边的孩子更大,j就选择右边孩子 if temp < li[j]: li[i] = li[j] i = j j = 2 * i + 1 else: # 退出循环条件:temp的值大于两个孩子的值 li[i] = temp break else: li[i] = temp def heapSort(li): # 建立堆 n = len(li) for i in range(n // 2 - 1, -1, -1):#从最后一个非叶子节点的下标位置开始循环 sift(li, i, n - 1) # 出数 for i in range(n - 1, -1, -1): li[i], li[0] = li[0], li[i] sift(li, 0, i - 1) li = [12, 58, 69, 2, 0, 5, 4, 3, 56] heapSort(li) print(li)#[0, 2, 3, 4, 5, 12, 56, 58, 69]
这是怎么实现的呢?
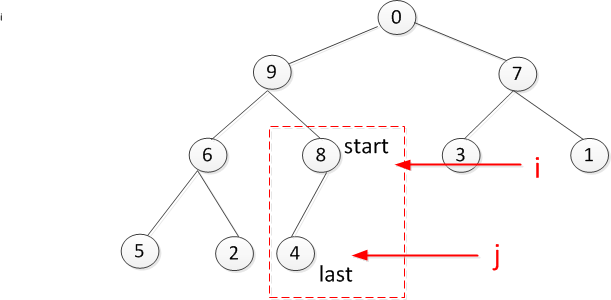
构建堆时是从最后一个叶子节点4开始,此时sift调整4,8的大小顺序,调整后接着循环,看叶子节点6是否符合要求
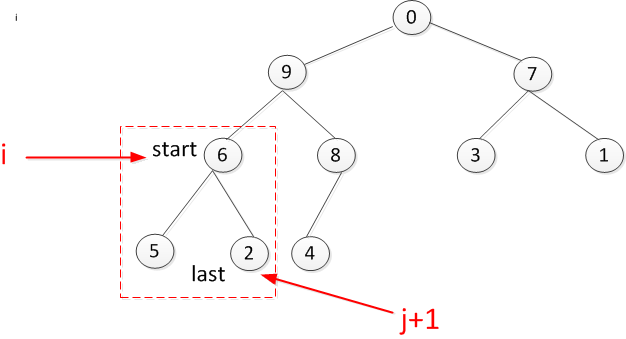
接着是叶子节点7是否符合要求
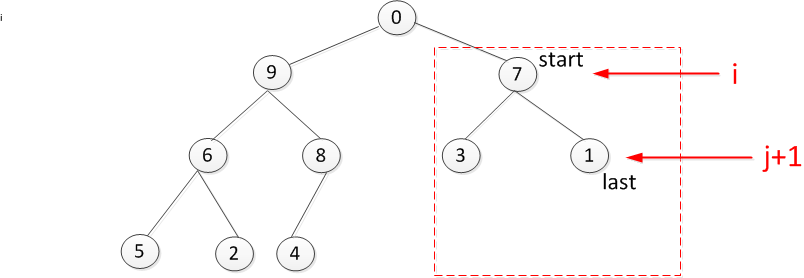
叶子节点9是否符合要求
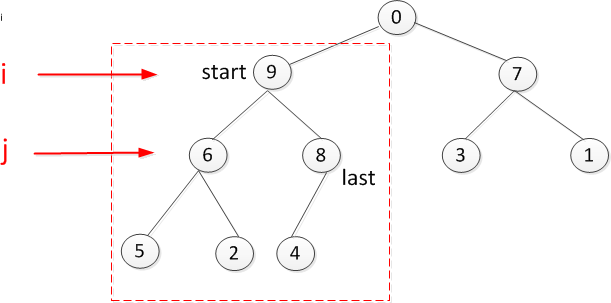
最后是根节点

这样就完成了堆排序的构建以及调整了,剩下的就是出数了,此时无须另外开辟空间,就在对结构的基础上进行就可以了,如下是调整后的堆:
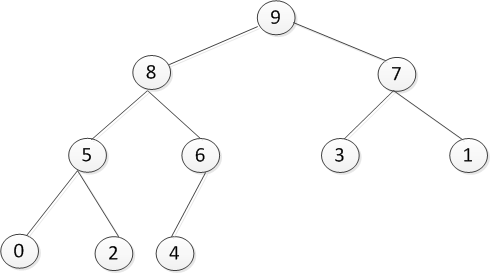
出数是首先将最后的4拿出来,然后将将顶部的9补上
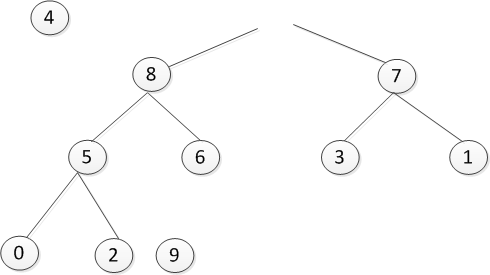
很明显4放不上,还需要进行调整,如下图所示:

每一个都是如此,最后的结果就是这样的:
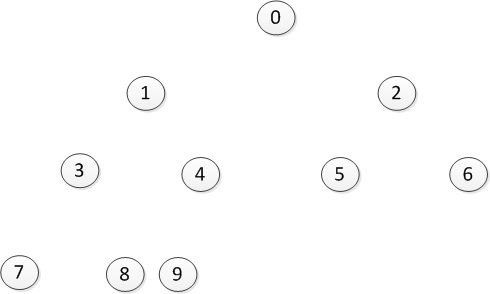
这就完成最终的出数,到此堆排序就完成了。
上面构造的是大顶堆,如果构建小顶堆,只需要修改sift函数的两个地方即可:
... while j <= last: # 退出循环条件:当前位置是叶子节点,j的位置超过了last if j + 1 <= last and li[j + 1] < li[j]: j = j + 1 # 如果右边的孩子更大,j就选择右边孩子 if temp > li[j]: li[i] = li[j] i = j ...
3、python内置堆排序
python已经有现成的堆排序,可以直接使用。
import heapq li = [12, 58, 69, 2, 0, 5, 4, 3, 56] heapq.heapify(li) #将列表中的数据转化为一个堆 print(li)#[0, 2, 4, 3, 58, 5, 69, 12, 56] ln=heapq.nsmallest(len(li),li) print(ln)#[0, 2, 3, 4, 5, 12, 56, 58, 69]
三、topK问题
现在有n个数,设计算法,找出前k大的数(k<n)
1、解决思路
- 取列表前k各元素,组成小顶堆,堆顶就是目前第k大的元素
- 依次遍历原列表后面的元素,如果元素小于堆顶元素,则忽略该元素;如果大于堆顶元素,则将堆顶更换为该元素,并且对堆进行一次调整
- 遍历列表剩余的所有元素后,倒序弹出堆项
只需要在上面的heapSort方法中,出数之前进行堆顶元素的置换以及堆的调整,此时heapSort方法除了传入这个序列,还需要传入k

def topK(li,k): heap=li[0:k] # 建立堆 for i in range(k//2-1,-1,-1): sift(heap,i,k-1) #顶部元素置换及调整堆 for i in range(k,len(li)): if li[i]>heap[0]: heap[0]=li[i] sift(heap,0,k-1) #出数 for i in range(k-1,-1,-1): heap[0],heap[i]=heap[i],heap[0] sift(heap,0,i-1)
2、利用python内置heapq
import heapq import random li=list(range(100)) random.shuffle(li) lm=heapq.nlargest(10,li) print(lm)#[99, 98, 97, 96, 95, 94, 93, 92, 91, 90]
