『图论』LCA最近公共祖先

概述篇

LCA（Least Common Ancestors），即最近公共祖先，是指这样的一个问题：在一棵有根树中，找出某两个节点 u 和 v 最近的公共祖先。

LCA可分为在线算法与离线算法

• 在线算法：指程序可以以序列化的方式一个一个处理输入，也就是说在一开始并不需要知道所有的输入。
• 离线算法：指一开始就需要知道问题的所有输入数据，而在解决一个问题后立即输出结果。

算法篇

对于该问题，很容易想到的做法是从 u、v 分别回溯到根节点，然后这两条路径中的第一个交点即为 u、v 的最近公共祖先，在一棵平衡二叉树中，该算法的时间复杂度可以达到(O(logn))，但是对于某些退化为链状的树来说，算法的时间复杂度最坏为(O(n))，显然无法满足更高频率的查询。

本节将介绍几种比较高效的算法来解决这一问题，常见的算法有三种：在线DFS+ST算法、倍增算法、离线Tarjan算法。

接下来我们来一一解释这两种的算法。

在线 DFS + ST 算法

首先看到 ST 你会想到什么呢？（脑补许久都没有想到它会是哪个单词的缩写）LCA的在线算法是可以建立在RMQ问题的基础上的

我们设 LCA(T,u,v) 为在有根树 T 中节点 u、v 的最近公共祖先， RMQ(A,i,j) 为线性序列 A 中区间 [i,j] 上的最小（大）值。

如下图这棵有根树：

我们令节点编号满足父节点编号小于子节点编号（编号条件）

可以看出 LCA(T,4,5) = 2, LCA(T,2,8) = 1, LCA(T,3,9) = 3 。

设线性序列 A 为有根树 T 的中序遍历，即 A = [4,2,5,1,8,6,9,3,7] 。

由中序遍历的性质我们可以知道，任意两点 u、v 的最近公共祖先总在以该两点所在位置为端点的区间内，且编号最小。

举个栗子：

假设 u = 8, v = 7 ，则该两点所确定的一段区间为 [8,6,9,3,7] ，而区间最小值为 3 ，也就是说，节点 3 为 u、v 的最近公共祖先。

解决区间最值问题我们可以采用RMQ问题中的 ST 算法 。

但是在有些问题中给出的节点并不一定满足我们所说的父节点编号小于子节点编号，因此我们可以利用节点间的关系建图，然后采用前序遍历来为每一个节点重新编号以生成线性序列 A ，于是问题又被转化为了区间最值的查询，和之前一样的做法咯~

时间复杂度：(n imes O(logn))预处理+$ O(1)$查询

(RMQ)问题的解法

---

以上部分介绍了LCA如何转化为RMQ问题，而在实际中这两种方案之间可以相互转化

类比之前的做法，我们如何将一个线性序列转化为满足编号条件的有根树呢？

1. 设序列中的最小值为(A_{k})，建立优先级为(A_{k})的根节点(T_{k})
2. 将(A[1...k−1])递归建树作为(T_{k})的左子树
3. 将(A[k+1...n])递归建树作为(T_{k})的右子树

读者可以试着利用此方法将之前的线性序列 A=[4,2,5,1,8,6,9,3,7] 构造出有根树 T ，结果一定满足之前所说的编号条件，但却不一定唯一。

离线 Tarjan 算法

Tarjan算法是一种常见的用于解决LCA问题的离线算法，它结合了深度优先搜索与并查集，整个算法为线性处理时间。

首先来介绍一下Tarjan算法的基本思路：

1. 任选一个节点为根节点，从根节点开始
2. 遍历该点u的所有子节点v，并标记v已经被访问过
3. 若v还有子节点，返回2，否则下一步
4. 合并v到u所在集合
5. 寻找与当前点u有询问关系的点e
6. 若e已经被访问过，则可以确定u、e的最近公共祖先为e被合并到的父亲节点

伪代码：

Tarjan(u)//merge和find为并查集合并函数和查找函数
{
    for each(u,v)//遍历u的所有子节点v
    {
        Tarjan(v);//继续往下遍历
        merge(u,v);//合并v到u这一集合
        标记v已被访问过;
    }
    for each(u,e)//遍历所有与u有查询关系的e
        if (e被访问过) u,e的最近公共祖先为find(e);
}

感觉讲到这里已经没有其它内容了，但是一定会有好多人没有理解怎么办呢？

我们假设在如下树中模拟Tarjan过程（节点数量少一点可以画更少的图）

存在查询： LCA(T,3,4)，LCA(T,4,6)，LCA(T,2,1) 。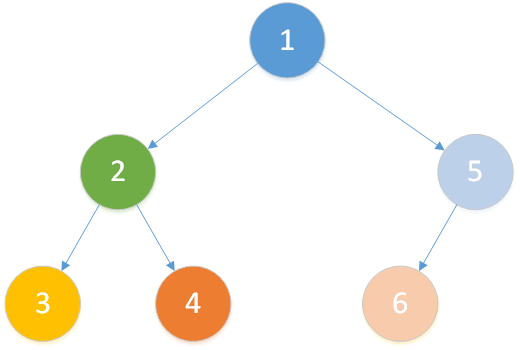

注意：每个节点的颜色代表它当前属于哪一个集合，橙色线条为搜索路径，黑色线条为合并路径。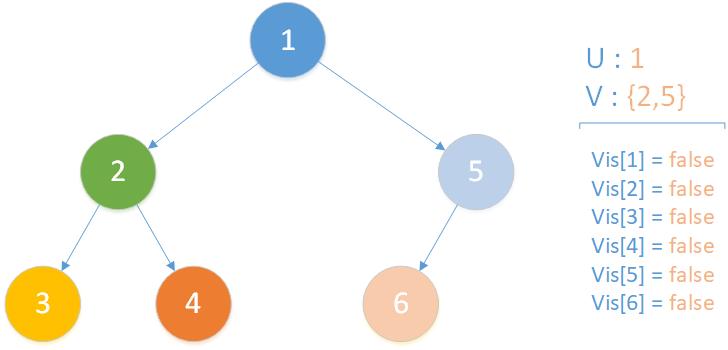

当前所在位置为 u = 1 ，未遍历孩子集合 v = {2,5} ，向下遍历。

当前所在位置为 u = 2 ，未遍历孩子集合 v = {3,4} ，向下遍历。

当前所在位置为 u = 3 ，未遍历孩子集合 v = {} ，递归到达最底层，遍历所有相关查询发现存在 LCA(T,3,4) ，但是节点 4 此时标记未访问，因此什么也不做，该层递归结束。

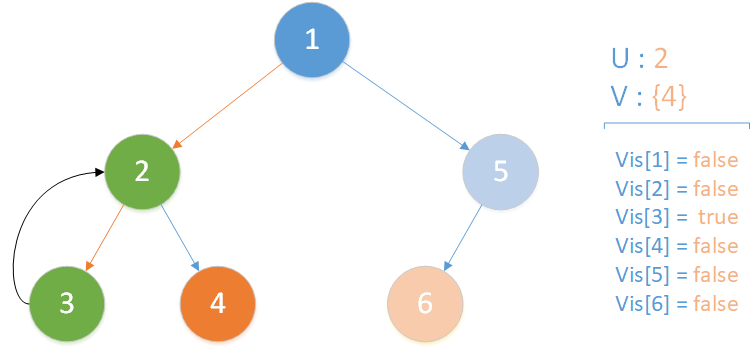
递归返回，当前所在位置 u = 2 ，合并节点 3 到 u 所在集合，标记 vis[3] = true ，此时未遍历孩子集合 v = {4} ，向下遍历。

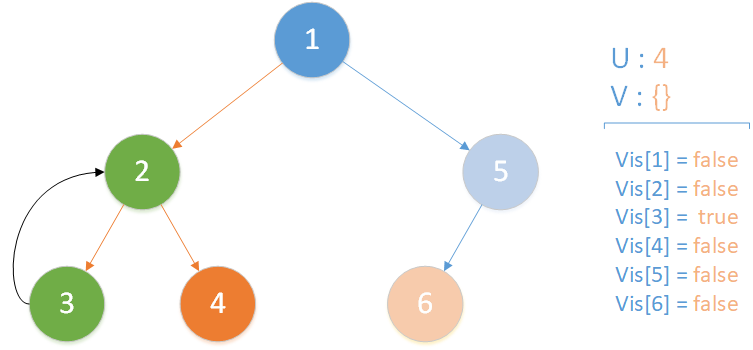
当前所在位置 u = 4 ，未遍历孩子集合 v = {} ，遍历所有相关查询发现存在 LCA(T,3,4) ，且 vis[3] = true ，此时得到该查询的解为节点 3 所在集合的首领，即 LCA(T,3,4) = 2 ；又发现存在相关查询 LCA(T,4,6) ，但是节点 6 此时标记未访问，因此什么也不做。该层递归结束。

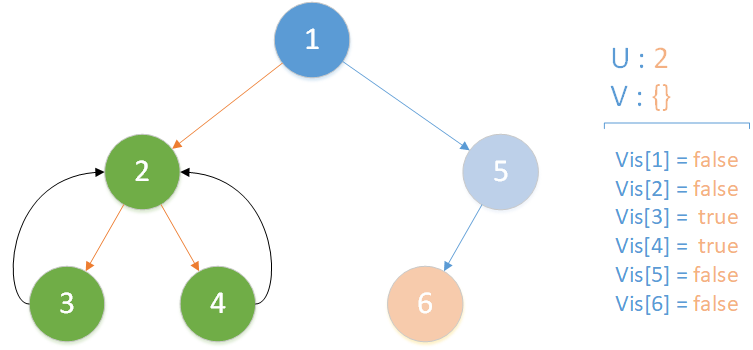
递归返回，当前所在位置 u = 2 ，合并节点 4 到 u 所在集合，标记 vis[4] = true ，未遍历孩子集合 v = {} ，遍历相关查询发现存在 LCA(T,2,1) ，但是节点 1 此时标记未访问，因此什么也不做，该层递归结束。

递归返回，当前所在位置 u = 1 ，合并节点 2 到 u 所在集合，标记 vis[2] = true ，未遍历孩子集合 v = {5} ，继续向下遍历。

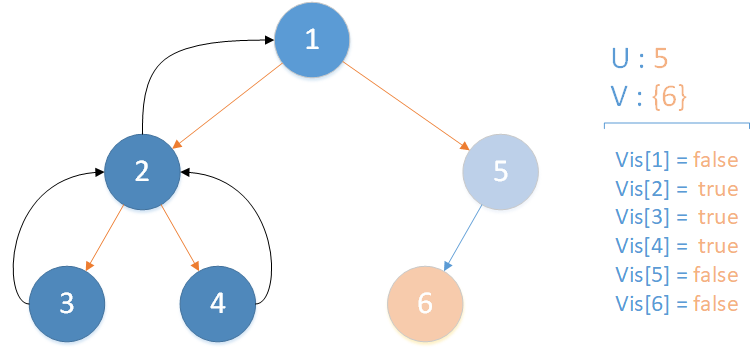
当前所在位置 u = 5 ，未遍历孩子集合 v = {6} ，继续向下遍历。

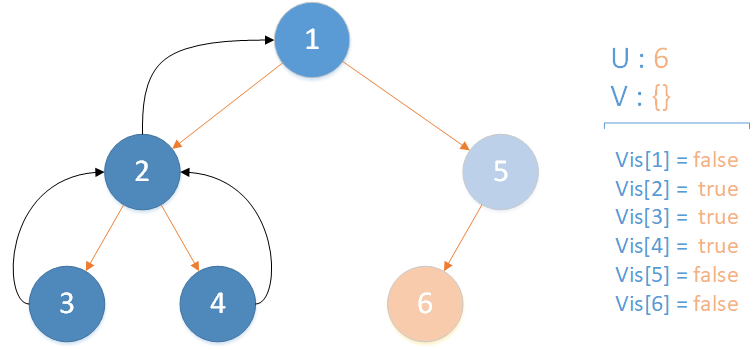
当前所在位置 u = 6 ，未遍历孩子集合 v = {} ，遍历相关查询发现存在 LCA(T,4,6) ，且 vis[4] = true ，因此得到该查询的解为节点 4 所在集合的首领，即 LCA(T,4,6) = 1 ，该层递归结束。

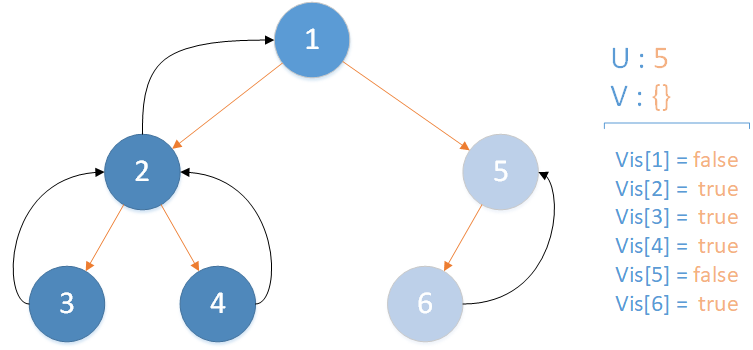
递归返回，当前所在位置 u = 5 ，合并节点 6 到 u 所在集合，并标记 vis[6] = true ，未遍历孩子集合 v = {} ，无相关查询因此该层递归结束。

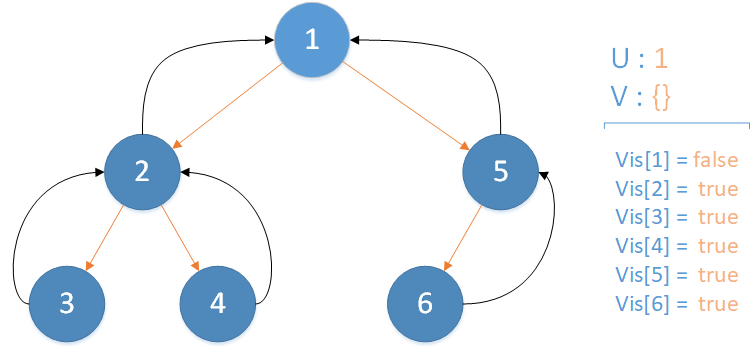
递归返回，当前所在位置 u = 1 ，合并节点 5 到 u 所在集合，并标记 vis[5] = true ，未遍历孩子集合 v = {} ，遍历相关查询发现存在 LCA(T,2,1) ，此时该查询的解便是节点 2 所在集合的首领，即 LCA(T,2,1) = 1 ，递归结束。

至此整个Tarjan算法便结束了

总结篇

对于不同的LCA问题我们可以选择不同的算法。

假若一棵树存在动态更新，此时离线算法就显得有点力不从心了，但是在其他情况下，离线算法往往效率更高。

另外， LCA和RMQ 问题是两个非常基础的问题，很多复杂问题都可以转化为这两类问题来解决。（当然这两类问题之间也可以相互转化）