PRML中,说到,概率图模型中,有向图的典型代表是贝叶斯网络,无向图模型的典型代表是马尔科夫随机场。
朴素贝叶斯其实是一种简单的贝叶斯网络。
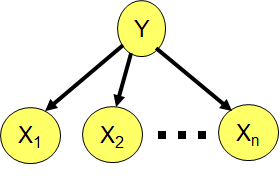
Priors P(Y) and conditionals P(Xi|Y) for Naïve Bayes provide CPTs for the network.
同时包含离散随机变量和连续随机变量的网络称为混合贝叶斯网络(hybrid Bayesian network)。
贝叶斯网络的精确推理:
(1)枚举法(低效,会重复计算)
(2)变量消元法
(3)团算法(也称“联合树”算法。基本思想是将网络中的单独节点联合起来形成团cluster节点)
大规模多连通网络中的精确推理(需要花费与网络规模呈线性关系的时间)是不可操作的,故,考虑近似的推理方法是必要的。随机采样算法,也称蒙特卡洛算法(Monte Carlo algorithm)能够给出一个问题的近似解答,而其近似的精度依赖于所生成采样点的多少。
模拟退火算法就是一种用于优化问题的蒙特卡洛算法。
贝叶斯网络的近似推理:
应用于后验概率计算的采样方法的两个算法族:
(1)直接采样方法
a. 拒绝采样(Rejection sampling):reject samples disagreeing with evidence.
这是一类由一个易于采样的分布出发,为一个难以直接采样的分布产生采样样本的通用算法。首先,它根据网络指定的先验概率分布生成采样样本;然后,它拒绝所有与证据不匹配的样本;最后通过在剩余样本中对事件X=x的出现频繁程度计数从而得到估计概率 P(X=x|e)。
存在的最大问题:它拒绝了太多的样本!随着证据变量个数的增多,与证据e 相一致的样本再所有样本中所占的比例呈指数下降,所以对于复杂问题这种方法是完全不可用的。
注意拒绝采样方法与直接根据现实世界对条件概率进行估计的过程非常相似。
例如,要估计 P(Rain | RedSkyAtNight=true)(晚上出现红色天空时,第二天下雨的概率分布),我们可以简单地对前一天晚上观察到红色天空后下雨的频度计数——而忽略天空不红的那些夜晚。(这里,现实世界本身扮演了采样生成算法的角色)。显然,如果天空很少发红,这个过程可能要花很长时间,而这就是拒绝采样方法的弱点。
b. 似然加权(Likelihood weighting):use evidence to weight samples.
只生成与证据 e 一致的事件,从而避免拒绝采样算法的低效率。它固定证据变量 E 的值,只对证据以外的其余变量X和Y进行采样,这保证了生成的每个采样样本都与证据一致。
(2)马尔科夫链采样方法
Markov Chain Monte Carlo(MCMC):sample from a stochastic process whose stationary distribution is the true posterior.
MCMC方法的随机近似技术能够提供对网络的真实后验概率的合理统计,并能够处理比精确算法规模大得多的网络。
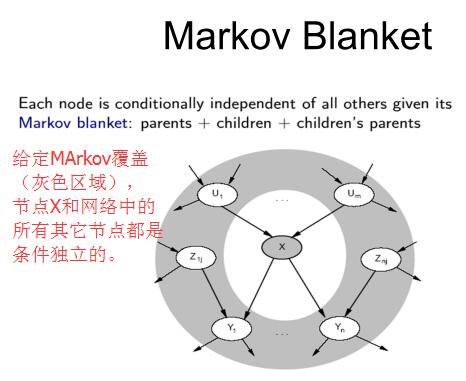
相比于直接采样的拒绝采样和似然加权这两种为每个事件都重新生成样本的采样算法不同,MCMC算法总是通过对前一个事件进行随机改变而生成每个事件样本。因此可以认为网络处于为每一个变量指定了值的一个特定的当前状态;而下一个状态则通过对某个非证据变量X_i进行采样来产生,取决于X_i的马尔科夫覆盖中的变量当前值。(单变量马尔科夫覆盖是由节点的父节点、子节点以及子节点的父节点组成的。the Markov blanket for a node in a Bayesian network is the set of nodes composed of its parents, its children, and its children‘s other parents.)
如下图:给定MArkov覆盖(灰色区域),节点X和网络中的所有其它节点都是条件独立的。
采样的例子:π的计算
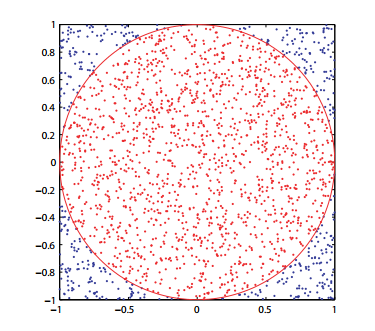
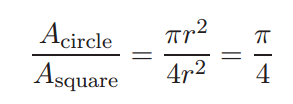
计算机采样:也称Monte Carlo
采样需要用随机数发生器,比如上图需要一个产生0-1 间的随机数发生器。
马尔可夫链的数学描述:马尔可夫链是一种简化的随机过程,假设一个状态只依赖于前一状态(称为马尔可夫性质)
吉布斯采样是一个简单的并且广泛应用的马尔科夫链蒙特卡洛(MCMC)算法,可以被看做Metropolis-Hastings算法的一个具体的情形。
MCMC算法执行过程示例:
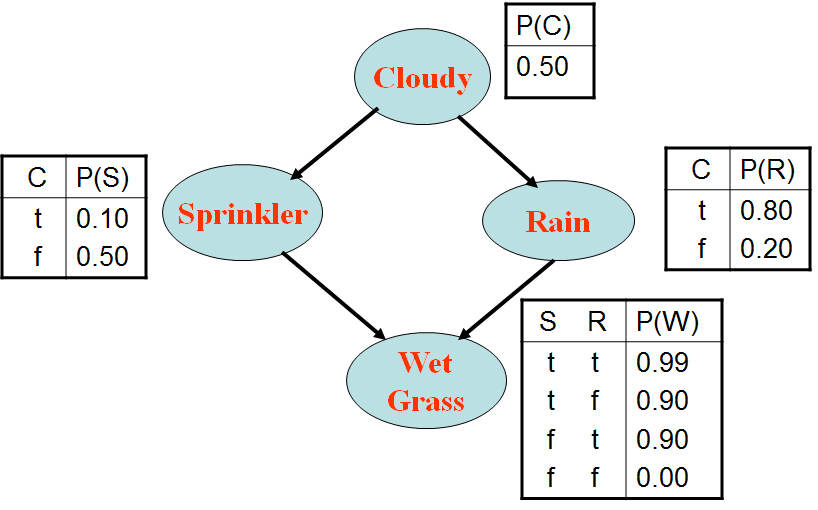
【要求】:计算P(Rain | Sprinkler = true, WetGrass = true)的概率
MCMC算法执行步骤:
- 证据变量Sprinkler, WetGrass固定为true
- 隐变量Cloudy和查询变量Rain随机初始化,例如,Cloudy = true, Rain = false,初始状态为:[C=true,S=true,R=false,W=true]
3. 反复执行如下步骤:
(1)根据Cloudy的马尔可夫覆盖(MB)变量的当前值,对Cloudy采样,即根据P(Cloudy|Sprinkler= true, Rain=false)来采样:
P(C|S, ~R) = P(C,S,~R) / P(S, ~R)
= P(C)P(S|C)P(~R|C) / [P(C)P(S|C)P(~R|C)+P(~C)P(S|~C)P(~R|~C)]
=(0.5´0.1´0.2) / [0.5´0.1´0.2+0.5´ 0.5´0.8]
=0.04762
假设采样结果为:Cloudy = false。故新的当前状态为:
[C=false, S=true, R=false, W=true]
(2)根据Rain节点的马尔可夫覆盖(MB)变量的当前值,对Rain采样,即根据P(Rain | Cloudy = false, Sprinkler = true, WetGrass = true)来采样。假设采样结果为:Rain = true。故新的当前状态为:
[C=false, S=true, R=true, W=true]
【注】: 上述过程中所访问的每一个状态都是一个样本,能对查询变量Rain的估计有贡献。
(3)重复上述步骤,直到所要求的访问次数N。
若为true, false的次数分别为n1, n2,则查询解为:
Normalize(<n1, n2>) = < n1 /N, n1 /N>
若上述过程访问了20个Rain=true的状态和60个Rain = false的状态,则所求查询的解为<0.25, 0.75>。
【References】
[1] Artificial Intelligence _A Modern Approach(Second Edition)
[2] Pattern Recognition and Machine Learning