Python实现梯度下降法

梯度下降法是机器学习算法更新模型参数的常用的方法之一。

【一些基本概念】

• 梯度 : 表示某一函数在一点处变化率最快的方向向量(可理解为这点的导数/偏导数)
• 样本 : 实际观测到的数据集，包括输入和输出(本文的样本数量用 m 表述,元素下标 i 表示)
• 特征 : 样本的输入(本文的特征数量用 n 表示,元素下标 j 表示)
• 假设函数 : 用来拟合样本的函数，记为 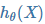(θ 为参数向量, X 为特征向量)
• 损失函数 : 用于评估模型拟合的程度，训练的目标是最小化损失函数，记为 J(θ)
  

• 线性假设函数 : 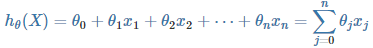     其中 X 为特征向量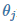，为模型参数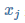，是特征向量的第 j 个元素(令x0=1)。

•  经典的平方差损失函数如下：

　　

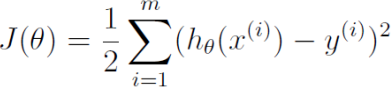
其中 m 为样本个数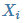，为样本特征集合的第 i 个元素（是一个向量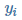），是样本输出的第 i 个元素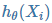，是假设函数。

【梯度下降法】

Goal：通过合理的方法更新假设函数 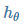 的参数 θ 使得损失函数 J(θ) 对于所有样本最小化。

步骤：

• 根据经验设计假设函数和损失函数，以及假设函数所有 θ  的初始值
• 对损失函数求所有 θ 的偏导（梯度）: 

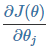
• 使用样本数据更新假设函数的 θ ，更新公式为：

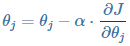
  其中 α  为更新步长（调整参数的灵敏度，灵敏度太高容易振荡，灵敏度过低收敛缓慢）

 <批量梯度下降算法>

 由之前所述，求Θ^T的问题演变成了求J(Θ)的极小值问题，这里使用梯度下降法。而梯度下降法中的梯度方向由J(Θ)对Θ的偏导数确定，由于求的是极小值，因此梯度方向是偏导数的反方向。

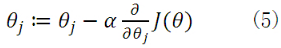
 公式(5)中α为学习速率，当α过大时，有可能越过最小值，而α当过小时，容易造成迭代次数较多，收敛速度较慢。

假如数据集中只有一条样本，那么样本数量，所以公式(5)中的求导为：

     

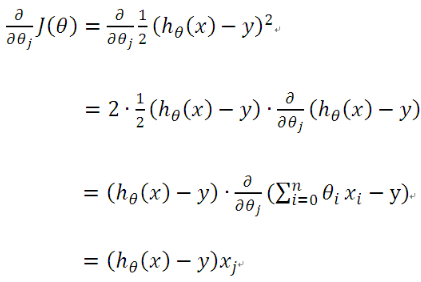
  于是公式(5)就演变成：

       

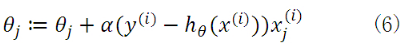
当样本数量m不为1时，将公式(5)中由公式(4)带入求偏导，那么每个参数沿梯度方向的变化值由公式(7)求得。

      

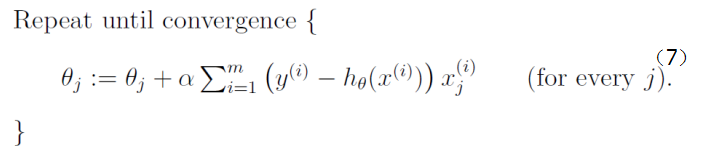
初始时Θ^T可设为，然后迭代使用公式(7)计算Θ^T中的每个参数，直至收敛为止。由于每次迭代计算Θ^T时，都使用了整个样本集，因此我们称该梯度下降算法为批量梯度下降算法(batch gradient descent)。

 <随机梯度下降算法>

 当样本集数据量m很大时，批量梯度下降算法每迭代一次的复杂度为O(mn),复杂度很高。因此，为了减少复杂度，当m很大时，我们更多时候使用随机梯度下降算法(stochastic gradient descent)，算法如下所示：

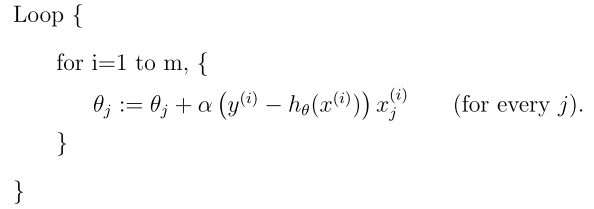
即每读取一条样本，就迭代对Θ^T进行更新，然后判断其是否收敛，若没收敛，则继续读取样本进行处理，如果所有样本都读取完毕了，则循环重新从头开始读取样本进行处理。

这样迭代一次的算法复杂度为O(n)。对于大数据集，很有可能只需读取一小部分数据，函数J(Θ)就收敛了。比如样本集数据量为100万，有可能读取几千条或几万条时，函数就达到了收敛值。所以当数据量很大时，更倾向于选择随机梯度下降算法。

但是，相较于批量梯度下降算法而言，随机梯度下降算法使得J(Θ)趋近于最小值的速度更快，但是有可能造成永远不可能收敛于最小值，有可能一直会在最小值周围震荡，但是实践中，大部分值都能够接近于最小值，效果也都还不错。

 <算法收敛判断方法>

• 参数Θ^T的变化距离为0，或者说变化距离小于某一阈值（Θ^T中每个参数的变化绝对值都小于一个阈值）。为减少计算复杂度，该方法更为推荐使用。
• J(Θ)不再变化，或者说变化程度小于某一阈值。计算复杂度较高，但是如果为了精确程度，那么该方法更为推荐使用。

<梯度下降算法的优缺点>

第一种，遍历全部数据集算一次损失函数，然后算函数对各个参数的梯度，更新梯度。这种方法每更新一次参数都要把数据集里的所有样本都看一遍，计算量开销大，计算速度慢，不支持在线学习，这称为Batch gradient descent，批梯度下降。慢但准确度好

另一种，每看一个数据就算一下损失函数，然后求梯度更新参数，这个称为随机梯度下降，stochastic gradient descent。这个方法速度比较快，但是收敛性能不太好，可能在最优点附近晃来晃去，hit不到最优点。两次参数的更新也有可能互相抵消掉，造成目标函数震荡的比较剧烈。快但准确度欠缺

为了克服两种方法的缺点，现在一般采用的是一种折中手段，mini-batch gradient decent，小批的梯度下降，这种方法把数据分为若干个批，按批来更新参数，这样，一个批中的一组数据共同决定了本次梯度的方向，下降起来就不容易跑偏，减少了随机性。另一方面因为批的样本数与整个数据集相比小了很多，计算量也不是很大。

 【Python代码实现如下】（基于Python 3.X ）

# !/usr/bin/env python
# encoding: utf-8
__author__ = 'Administrator'

#梯度下降法的目标是通过合理的方法更新假设函数 hθ 的参数 θ 使得损失函数 J(θ) 对于所有样本最小化。
# 这个合理的方法的步骤如下:
#
# 根据经验设计假设函数和损失函数，以及假设函数所有 θ 的初始值
# 对损失函数求所有 θ 的偏导（梯度）: ∂J(θ)/∂θj
# 使用样本数据更新假设函数的 θ，更新公式为: θj=θj−α⋅∂J/∂θj (其中 α 为更新步长（调整参数的灵敏度，灵敏度太高容易振荡，灵敏度过低收敛缓慢）

import numpy as np
import matplotlib.pyplot as plt

def GD1():
    spaces = [45, 73, 89, 120, 140, 163]
    prices = [80, 150, 198, 230, 280, 360]
    spaces, prices = np.array(spaces), np.array(prices)  # numpy.array:使用列表生成一维数组

    # #-------画出房屋面积与房屋价格的散点图
    # plt.scatter(spaces,prices,c="g")
    # plt.xlabel("house space")
    # plt.ylabel("house price")
    # plt.show()

    # 设置theta的初始值
    theta0 = 0
    theta1 = 0

    # 选择步长alpha：如果步长选择不对，则theta参数更新结果可能会不对
    alpha = 0.00005
    # 当α过大时，有可能越过最小值，而α当过小时，容易造成迭代次数较多，收敛速度较慢。

    x_i0 = np.ones(len(spaces))  # 返回一个用1 填充的数组，一个参数表示这行的元素个数np.ones(5)：一行5列。np.ones((2, 1))：两行一列，都是1

    # 所以是返回一个有6个元素的一组数组
    # 假设函数h(x):
    def h(x):
        return theta0 + theta1 * x  # 一个x为一个特征

    # 损失函数
    def calc_error():
        return np.sum(np.power((h(spaces) - prices), 2)) / 2

    # 损失函数偏导数 （theta 0 和theta 1）
    def calc_delta0():
        return alpha * np.sum(h(spaces) - prices) * x_i0

    def calc_delta1():
        return alpha * np.sum(h(spaces) - prices) * spaces

    # 循环更新 theta 值并计算误差，停止条件为：
    #  1.误差小于某个值
    #  2.循环次数控制
    k = 0
    while True:
        delta0 = calc_delta0()
        delta1 = calc_delta1()
        theta0 = theta0 - delta0
        theta1 = theta1 - delta1
        error = calc_error()
        # print("delta [%f,%f],theta [%f,%f], error %f" % (delta0,delta1,theta0,theta1,error))
        print()

        k = k + 1
        if (k > 10 or error < 200):
            break
    # print("h(x)=%f + %f * x"%(theta0,theta1))

    # print('h(x)={}+{}*x'.format(theta0, theta1))
    # 使用假设函数计算出来的价格，用于画拟合曲线
    y_out = h(spaces)

    plt.scatter(spaces, prices, c="g")  # 绿色点表示房屋面积和价格数据的散点图
    plt.plot(spaces, y_out, c="b")  # 蓝色点表示使用梯度下降法拟合出来的曲线
    plt.xlabel("house space")
    plt.ylabel("house price")
    plt.show()
# GD1()


def GD2():
    # Training data set
    # each element in x represents (x1)
    x = [1, 2, 3, 4, 5, 6]
    # y[i] is the output of y =theta0 + theta1*x[1]
    y = [13, 14, 20, 21, 25, 30]
    # 设置允许误差值
    epsilon = 1
    # 学习率
    alpha = 0.01

    diff = [0, 0]
    max_itor = 20

    error0 = 0
    error1 = 0

    count = 1
    m = len(x)

    # init the parameters to zero
    theta0 = 0
    theta1 = 0
    error_list = []
    while 1:

        count = count + 1
        diff = [0, 0]
        for i in range(m):
            diff[0] += theta0 + theta1 * x[i] - y[i]
            diff[1] += (theta0 + theta1 * x[i] - y[i]) * x[i]
        theta0 = theta0 - alpha / m * diff[0]
        theta1 = theta0 - alpha / m * diff[1]
        error1 = 0

        for i in range(m):
            error1 += (theta0 + theta1 * x[i] - y[i]) ** 2
        error_list.append(error1)
        if abs(error1 - error0) < epsilon:
            break

        print("iterator :%d theta0 :%f,theta1 :%f,error:%f" % (count-1,theta0, theta1, error1))
        if count > 100:
            print("count>100...")
            break
    print("theta0 :%f,theta1 :%f,error:%f" % (theta0, theta1, error1))
    print("error_list为：",error_list)
    #-----画收敛散点图--
    # plt.scatter(x,y,c="g")
    n=len(error_list)
    ite=range(n)
    plt.plot(ite,error_list,c="r",linewidth=3)
    plt.title("Convergence curve")
    plt.xlabel("iteration")
    plt.ylabel("error")
    plt.show()

GD2()

 GD2()运行结果为：

 

损失函数的收敛曲线图：

 

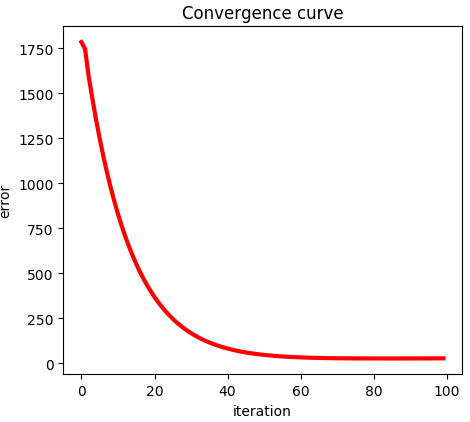
【Reference】

1. http://blog.lisp4fun.com/2017/11/02/gradient-desent

2. http://www.cnblogs.com/eczhou/p/3951861.html

3. http://blog.csdn.net/l18930738887/article/details/50670370