为什么可以通过给目标函数增加一个正则项来防止其过拟合?(来使其更圆滑?)
(在实现MF矩阵分解算法的时候,也有给损失函数增加一个正则项:推荐系统之矩阵分解及其Python代码实现)
经常用来控制过拟合现象的一种技术是正则化(regularization)。
这种技术涉及到给误差函数增加一个惩罚项,使得系数不会达到很大的值。
这种惩罚项最简单的形式采用所有系数的平方和的形式。
误差函数的修改后的形式:
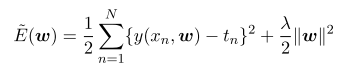 (可以用解析的形式求出最小值)
(可以用解析的形式求出最小值)
其中,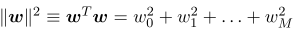
系数 λ 控制了正则化项相对于平方和误差项的重要性。
像这样的技术在统计学的文献中被叫做收缩(shrinkage)方法,因为这种方法减小了系数的值。
二次正则项的一个特殊情况被称为山脊回归(ridge regression)(Hoerl and Kennard, 1970)。
在神经网络的情形中,这种方法被叫做权值衰减(weight decay)。
另外,避免过拟合的其他方法有:
1)early stopping;
:记录到目前最好的值, 可以看loss,也可以看测评指标, 连续多少次迭代都没有超过这个最好值就可以停了。
与增加一个正则项的方法有什么本质区别?
—— 增加一个正则项的方法:是避免参数过拟合(约束所有的参数不过拟合,但是参数组合以后的情况不可预料的。
—— early stopping是从结果上看的,
2)增大数据集的规模;
正则化(Regularization)包括L1、L2(L2 regularization也叫weight decay);
3)dropout(为了防止神经网络中出现的过拟合);
【Reference】
2、PRML