Learning to Rank：Point-wise、Pair-wise 和 List-wise区别

 机器学习的 ranking 技术——learning2rank，包括 pointwise、pairwise、listwise 三大类型。

 

【Ref-1】给出的：

<Point wise ranking 类似于回归>

Point wise ranking is analogous to regression. Each point has an associated rank score, and you want to predict that rank score. So your labeled data set will have a feature vector and associated rank score given a query

IE: {d1, r1} {d2, r2} {d3, r3} {d4, r4}

where r1 > r2 > r3 >r4

 

<Pairwise ranking 类似于分类>

Pairwise ranking is analogous to classification. Each data point is associated with another data point, and the goal is to learn a classifier which will predict which of the two is "more" relevant to a given query.

IE: {d1 > d2} {d2 > d3} {d3 > d4}

 

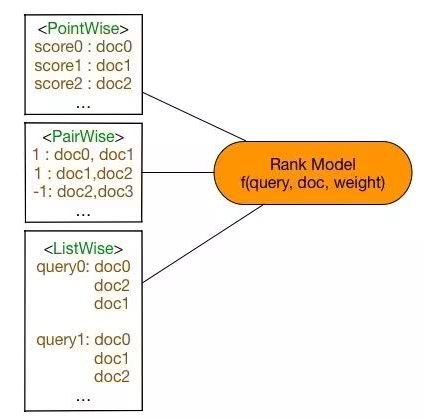
  1、Pointwise Approach

　　1.1 特点

　　Pointwise 类方法，其 L2R 框架具有以下特征：

• 输入空间中样本是单个 doc（和对应 query）构成的特征向量；
• 输出空间中样本是单个 doc（和对应 query）的相关度；
• 假设空间中样本是打分函数；
• 损失函数评估单个 doc 的预测得分和真实得分之间差异。

　　这里讨论下，关于人工标注标签怎么转换到 pointwise 类方法的输出空间：

1. 如果标注直接是相关度 s_j，则 doc x_j 的真实标签定义为 y_j=s_j
2. 如果标注是 pairwise preference s_{u,v}，则 doc x_j 的真实标签可以利用该 doc 击败了其他 docs 的频次
3. 如果标注是整体排序 π，则 doc x_j 的真实标签可以利用映射函数，如将 doc 的排序位置序号当作真实标签

　　1.2  根据使用的 ML 方法不同，pointwise 类可以进一步分成三类：基于回归的算法、基于分类的算法，基于有序回归的算法。

　　（1）基于回归的算法

　　　　此时，输出空间包含的是实值相关度得分。采用 ML 中传统的回归方法即可。

　　（2）基于分类的算法

　　　　此时，输出空间包含的是无序类别。对于二分类，SVM、LR 等均可；对于多分类，提升树等均可。

　　（3）基于有序回归的算法

　　　　此时，输出空间包含的是有序类别。通常是找到一个打分函数，然后用一系列阈值对得分进行分割，得到有序类别。采用 PRanking、基于 margin 的方法都可以。

　　1.3  缺陷  

　　　　回顾概述中提到的评估指标应该基于 query 和 position，

• ranking 追求的是排序结果，并不要求精确打分，只要有相对打分即可。
• pointwise 类方法并没有考虑同一个 query 对应的 docs 间的内部依赖性。一方面，导致输入空间内的样本不是 IID 的，违反了 ML 的基本假设，另一方面，没有充分利用这种样本间的结构性。其次，当不同 query 对应不同数量的 docs 时，整体 loss 将会被对应 docs 数量大的 query 组所支配，前面说过应该每组 query 都是等价的。
• 损失函数也没有 model 到预测排序中的位置信息。因此，损失函数可能无意的过多强调那些不重要的 docs，即那些排序在后面对用户体验影响小的 doc。

　　1.4  改进

　　　　如在 loss 中引入基于 query 的正则化因子的 RankCosine 方法。

  

  2、Pairwise Approach

　   2.1 特点

　　Pairwise 类方法，其 L2R 框架具有以下特征：

• 输入空间中样本是（同一 query 对应的）两个 doc（和对应 query）构成的两个特征向量；
• 输出空间中样本是 pairwise preference；
• 假设空间中样本是二变量函数；
• 损失函数评估 doc pair 的预测 preference 和真实 preference 之间差异。

　　这里讨论下，关于人工标注标签怎么转换到 pairwise 类方法的输出空间：

1. 如果标注直接是相关度 s_j，则 doc pair (x_u,x_v) 的真实标签定义为 y_{u,v}=2*I_{s_u>s_v}-1
2. 如果标注是 pairwise preference s_{u,v}，则 doc pair (x_u,x_v) 的真实标签定义为y_{u,v}=s_{u,v}
3. 如果标注是整体排序 π，则 doc pair (x_u,x_v) 的真实标签定义为y_{u,v}=2*I_{π_u,π_v}-1

　　2.2  基于二分类的算法　　

　　Pairwise 类方法基本就是使用二分类算法即可。

　　经典的算法有 基于 NN 的 SortNet，基于 NN 的 RankNet，基于 fidelity loss 的 FRank，基于 AdaBoost 的 RankBoost，基于 SVM 的 RankingSVM，基于提升树的 GBRank。

　　2.3  缺陷  

　　虽然 pairwise 类相较 pointwise 类 model 到一些 doc pair 间的相对顺序信息，但还是存在不少问题，回顾概述中提到的评估指标应该基于 query 和 position，

• 如果人工标注给定的是第一种和第三种，即已包含多有序类别，那么转化成 pairwise preference 时必定会损失掉一些更细粒度的相关度标注信息。
• doc pair 的数量将是 doc 数量的二次，从而 pointwise 类方法就存在的 query 间 doc 数量的不平衡性将在 pairwise 类方法中进一步放大。
• pairwise 类方法相对 pointwise 类方法对噪声标注更敏感，即一个错误标注会引起多个 doc pair 标注错误。
• pairwise 类方法仅考虑了 doc pair 的相对位置，损失函数还是没有 model 到预测排序中的位置信息。
• pairwise 类方法也没有考虑同一个 query 对应的 doc pair 间的内部依赖性，即输入空间内的样本并不是 IID 的，违反了 ML 的基本假设，并且也没有充分利用这种样本间的结构性。

　　2.4  改进

　　　pairwise 类方法也有一些尝试，去一定程度解决上述缺陷，比如：

• Multiple hyperplane ranker，主要针对前述第一个缺陷
• magnitude-preserving ranking，主要针对前述第一个缺陷
• IRSVM，主要针对前述第二个缺陷
• 采用 Sigmoid 进行改进的 pairwise 方法，主要针对前述第三个缺陷
• P-norm push，主要针对前述第四个缺陷
• Ordered weighted average ranking，主要针对前述第四个缺陷
• LambdaRank，主要针对前述第四个缺陷
• Sparse ranker，主要针对前述第四个缺陷

  　3、Listwise Approach

　　3.1 特点　　

　　Listwise 类方法，其 L2R 框架具有以下特征：

• 输入空间中样本是（同一 query 对应的）所有 doc（与对应的 query）构成的多个特征向量（列表）；
• 输出空间中样本是这些 doc（和对应 query）的相关度排序列表或者排列；
• 假设空间中样本是多变量函数，对于 docs 得到其排列，实践中，通常是一个打分函数，根据打分函数对所有 docs 的打分进行排序得到 docs 相关度的排列；
• 损失函数分成两类，一类是直接和评价指标相关的，还有一类不是直接相关的。具体后面介绍。

　　这里讨论下，关于人工标注标签怎么转换到 listwise 类方法的输出空间：

1. 如果标注直接是相关度 s_j，则 doc set 的真实标签可以利用相关度 s_j 进行比较构造出排列
2. 如果标注是 pairwise preference s_{u,v}，则 doc set 的真实标签也可以利用所有 s_{u,v} 进行比较构造出排列
3. 如果标注是整体排序 π，则 doc set 则可以直接得到真实标签

 

　　3.2  根据损失函数构造方式的不同，listwise 类可以分成两类直接基于评价指标的算法，间接基于评价指标的算法。

　　　（1）直接基于评价指标的算法

　　直接取优化 ranking 的评价指标，也算是 listwise 中最直观的方法。但这并不简单，因为前面说过评价指标都是离散不可微的，具体处理方式有这么几种：

• 优化基于评价指标的 ranking error 的连续可微的近似，这种方法就可以直接应用已有的优化方法，如SoftRank，ApproximateRank，SmoothRank
• 优化基于评价指标的 ranking error 的连续可微的上界，如 SVM-MAP，SVM-NDCG，PermuRank
• 使用可以优化非平滑目标函数的优化技术，如 AdaRank，RankGP

　　上述方法的优化目标都是直接和 ranking 的评价指标有关。现在来考虑一个概念，informativeness。通常认为一个更有信息量的指标，可以产生更有效的排序模型。而多层评价指标（NDCG）相较二元评价（AP）指标通常更富信息量。因此，有时虽然使用信息量更少的指标来评估模型，但仍然可以使用更富信息量的指标来作为 loss 进行模型训练。

　　   （2）非直接基于评价指标的算法

　　这里，不再使用和评价指标相关的 loss 来优化模型，而是设计能衡量模型输出与真实排列之间差异的 loss，如此获得的模型在评价指标上也能获得不错的性能。 
　　经典的如 ，ListNet，ListMLE，StructRank，BoltzRank。

　　3.3  缺陷  

listwise 类相较 pointwise、pairwise 对 ranking 的 model 更自然，解决了 ranking 应该基于 query 和 position 问题。

listwise 类存在的主要缺陷是：一些 ranking 算法需要基于排列来计算 loss，从而使得训练复杂度较高，如 ListNet和 BoltzRank。此外，位置信息并没有在 loss 中得到充分利用，可以考虑在 ListNet 和 ListMLE 的 loss 中引入位置折扣因子。

　　3.4  改进

　　　pairwise 类方法也有一些尝试，去一定程度解决上述缺陷，比如：

• Multiple hyperplane ranker，主要针对前述第一个缺陷
• magnitude-preserving ranking，主要针对前述第一个缺陷
• IRSVM，主要针对前述第二个缺陷
• 采用 Sigmoid 进行改进的 pairwise 方法，主要针对前述第三个缺陷
• P-norm push，主要针对前述第四个缺陷
• Ordered weighted average ranking，主要针对前述第四个缺陷
• LambdaRank，主要针对前述第四个缺陷
• Sparse ranker，主要针对前述第四个缺陷

以上，这三大类方法主要区别在于损失函数。不同的损失函数决定了不同的模型学习过程和输入输出空间。

rating数据集：

：所以关于这个问题，是要使用topN=1的对吗？并把指标改为 AUC和 NDCG对吗？

——是这样，这个是一个rating数据集。

如果是按照pairwise ranking的正确率，应该是我们的oPR和oMRR，PR和MAP都是没有用的。

如果不按照pairwise，（按照listwise），就是AUC和NDCG，所以我让你算那个。

当然还有就是按照数值，（按照pointwise），RMSE，不过我们的没法计算RMSE。

：啊这个“不按照pairwise”，没太明白，还是按照原来的思路，用的 winner 和 loser 比较对呀。尤其在这个rating数据集，是每个比较对当成一个session，这点还是不变的吧？？

——这不就是pairwise吗？

rating是可以按照每个用户得到一个排序的，这是listwise，也就是算出NDCG，AUC的指标。

还可以按照pointwise，每个分数预测的怎么样，就是RMSE。

 

【Reference】

1、What is the difference between point-wise and pair-wise ranking in machine learning

2、学习排序 Learning to Rank：从 pointwise 和 pairwise 到 listwise，经典模型与优缺点

3、基于 Pairwise 和 Listwise 的排序学习