本专题文章建立在本人多年写动态规划代码的经验上,用以自己回顾总结,也帮助朋友初步理解,部分理解可能和教科书有所出入,要参加算法考试的同学请以教科书为准。
概念引入
在现实生活中,有一类活动的过程,由于它的特殊性,可将过程分成若干个互相联系的阶段,在它的每一阶段都需要作出决策,从而使整个过程达到最好的活动效果。因此各个阶段决策的选取不能任意确定,它依赖于当前面临的状态,又影响以后的发展。当各个阶段决策确定后,就组成一个决策序列,因而也就确定了整个过程的一条活动路线.这种把一个问题看作是一个前后关联具有链状结构的多阶段过程就称为多阶段决策过程,这种问题称为多阶段决策问题。在多阶段决策问题中,各个阶段采取的决策,一般来说是与时间有关的,决策依赖于当前状态,又随即引起状态的转移,一个决策序列就是在变化的状态中产生出来的,故有“动态”的含义,称这种解决多阶段决策最优化的过程为动态规划方法[1]。
虽然这段话非常抽象,但它清晰地解释了动态规划(Dynamic Programming,下文简称DP)为什么“动态”。包括我在内的部分人认为DP不是一种算法而是一种方法或者说思想。我们通常认为算法是编程的方法论,那么DP这类的思想可以说是算法的方法论,比如著名的floyd多源最短路算法的核心思想就是DP。
动态规划首先是一个规划:给出一个规划问题,让求最优解或最优决策,比如说一个老板有多条生产线,如何分配产能得到最多的剩余价值,当然这个问题可以用高中学过的线性规划来解决。而我们为什么强调它是动态的,是因为它在不同步骤做决策时状态变了,且通常做的决策不能只顾当前,还要瞻前(DP的前效性)顾后(DP的后效性)。什么是状态?可以这样简单的理解,工厂各条生产线对应商品的市场价就是状态,我们做线性规划的前提是市场价不发生改变,可以规划出当下最优解。但如果市场价每天都发生变化,也就是说状态是在变的,那么这个规划问题就可以说是个动态规划问题。
如果看到这你感觉云里雾里的,没关系,可以在学了几种DP,写个十几道题之后再回头看概念。
这里把各个术语的定义[2]丢一下,可以先不看。
- 阶段:把所给求解问题的过程恰当地分成若干个相互联系的阶段,以便于求解,过程不同,阶段数就可能不同.描述阶段的变量称为阶段变量。在多数情况下,阶段变量是离散的,用k表示。此外,也有阶段变量是连续的情形。如果过程可以在任何时刻作出决策,且在任意两个不同的时刻之间允许有无穷多个决策时,阶段变量就是连续的。
- 状态:状态表示每个阶段开始面临的自然状况或客观条件,它不以人们的主观意志为转移,也称为不可控因素。在上面的例子中状态就是某阶段的出发位置,它既是该阶段某路的起点,同时又是前一阶段某支路的终点 。
- 无后效性:我们要求状态具有下面的性质:如果给定某一阶段的状态,则在这一阶段以后过程的发展不受这阶段以前各段状态的影响,所有各阶段都确定时,整个过程也就确定了。换句话说,过程的每一次实现可以用一个状态序列表示,在前面的例子中每阶段的状态是该线路的始点,确定了这些点的序列,整个线路也就完全确定。从某一阶段以后的线路开始,当这段的始点给定时,不受以前线路(所通过的点)的影响。状态的这个性质意味着过程的历史只能通过当前的状态去影响它的未来的发展,这个性质称为无后效性。
- 决策:一个阶段的状态给定以后,从该状态演变到下一阶段某个状态的一种选择(行动)称为决策。在最优控制中,也称为控制。在许多问题中,决策可以自然而然地表示为一个数或一组数。不同的决策对应着不同的数值。描述决策的变量称决策变量,因状态满足无后效性,故在每个阶段选择决策时只需考虑当前的状态而无须考虑过程的历史。
- 策略:由每个阶段的决策组成的序列称为策略。对于每一个实际的多阶段决策过程,可供选取的策略有一定的范围限制,这个范围称为允许策略集合。
简单线性DP
具有线性状态划分的动归称为线性DP,通常其状态转移也是线性的。
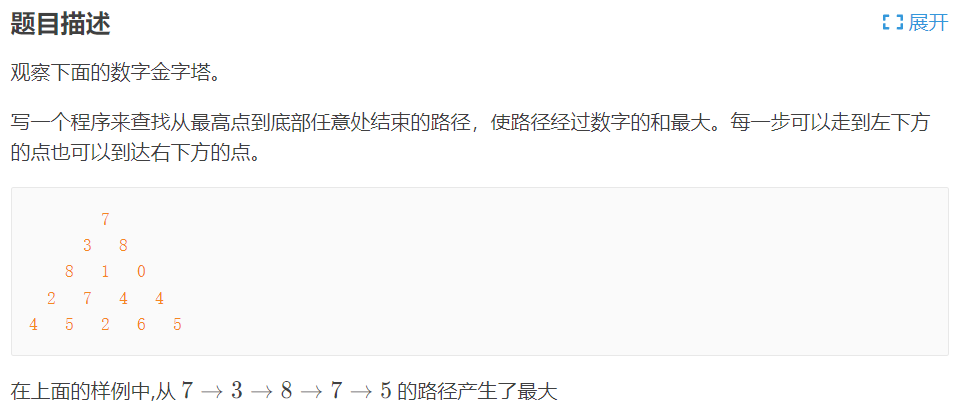
数塔问题
原题链接
这道题非常有来头,是1994年IOI(international olympiad in informatics)的题,当时DP还没怎么普及。DP普及之后,这道题在洛谷的难度被标为普及-,也就是还没达到初中生竞赛的难度。
如果不用DP,这道题该怎么做?搜索,把所有可以走的路枚举出来,找到所有路中的最优解。数塔有N层的,总共有几条路呢?有 \(2^{N-1}\) 条。也就是说算法的复杂度是 \(O(2^N)\) 的。这里放上DFS的代码:
点击查看代码
//Luogu P1216 coded by Jiayou
#include<iostream>
using namespace std;
int N, map[105][105];
int dfs(int floor,int pos){
//到达第floor层,第pos个数字
if(floor==N)
return map[floor][pos];
else
return max(dfs(floor + 1, pos), dfs(floor + 1, pos + 1)) + map[floor][pos];
}
int main(){
cin >> N;
for (int i = 1; i <= N;i++)
for (int j = 1; j <= i;j++)
cin >> map[i][j];
cout << dfs(1, 1);//从第一层第一个数字出发
}
这里 \(dfs(i,j)\) 的返回值的意义是什么呢?是走到第i层第j个的数字的时候,再往后走最多能取到几。所以全局的答案就是 \(dfs(1,1)\):已经走到第一个点,再往后走能娶到的最大值。问读者们一个问题:在我们深度优先搜索的时候,是不是会多次经过同一个点?会,因为深搜的顺序是按着路径走的,而这 \(2^{N-1}\) 条路径互相之间是存在共同经过的点的。所以形如 \(dfs(4,3)\) 这样的函数会被调用多次。那么再追问读者一下:前后两次调用 \(dfs(4,3)\) 获得的返回值相同吗?是相同的,因为 \(dfs(4,3)\) 表示走到这个点后再往后走的最大值,这个值是定值。那么我们是不是可以开一个数组 \(memory[105][105]\),第一次 \(dfs(4,3)\) 的时候,让 \(memory[4][3]=dfs(4,3)\)。之后如果还需要调用 \(dfs(4,3)\),发现之前已经计算过一次了,这次就不再重复计算,直接获取 \(memory[4][3]\) 的值。其实每个 \(dfs(i,j)\) 都是一个子问题,它们在搜索中可能被提出多次,这个叫做子问题重叠。对于重叠的子问题,记录下答案,下次出现时不再去计算它,就是记忆化搜索。记忆化搜索和DP本质上是相同的,任何使用DP方法的代码都可以改写成记忆化搜索,反之亦然。但使用DP可以简洁地使用代码表示出递推关系,易于优化,且避开了递归,程序运行效率更高。那么现在我们来改写这个P1216记忆化深搜。
既然算法变了,那我们把 \(memory\) 数组改名成 \(dp\) 数组(它们本质是相同的)。既 \(dp[i][j]\) 表示从 \((i,j)\) 这个点出发往下走能取到的最大值。问:\(dp[i][j]\) 的值由谁决定?由 \(dp[i+1][j]\) 和 \(dp[i+1][j+1]\) 决定,因为 \(dp[i][j]=max(dp[i+1][j],dp[i+1][j+1])+map[i][j]\) 从 \((i,j)\) 出发能获得的最大值,自然就下一步能获得的最大值加上 \(map[i][j]\) ,而下一步的最大值则是 \(max(dp[i+1][j],dp[i+1][j+1])\)。所以刚刚那个公式就是这么来的。这个公式揭示了记忆化搜索更新 \(dp\) 数组的顺序,也就是说,现在,我们不需要使用搜索算法,也可以算出整个 \(dp\)数组了。需要计算 \(dp[i][j]\), 就需要先计算 \(dp[i+1][j]\) 和 \(dp[i+1][j+1]\)。而数塔最底层对应dp值是非常好知道的,因为它不能再往下走了: \(dp[i][j] = map[i][j], when\space i=N\)。那么我们就可以先把最底层的dp算出来,然后算倒数第二层,最后算出第一层。第一层只有一个点,那个点的dp值就是答案。
代码:
点击查看代码
//Luogu P1216 coded by Jiayou
#include<iostream>
using namespace std;
int N, map[1005][1005];
int dp[1005][1005];
int main(){
cin >> N;
for (int i = 1; i <= N;i++)
for (int j = 1; j <= i;j++)
cin >> map[i][j];
for (int j = 1; j <= N;j++)
dp[N][j] = map[N][j];
for (int i = N - 1; i > 0;i--)
for (int j = 1; j <= N;j++)
dp[i][j] = max(dp[i + 1][j], dp[i + 1][j + 1]) + map[i][j];
cout << dp[1][1];
}
\(dp[i][j]=max(dp[i+1][j],dp[i+1][j+1])+map[i][j]\) 这个我们叫做状态转移方程。这里的状态就是 \((i,j)\),它表示走到第i层第j个点,这是既定的条件,我们的决策也是在这个状态下定制出来的。通俗的理解,状态就是一个数的集合,是你记忆化搜索的参数列表,是你的子问题的条件。状态转移就是通过已知解的状态计算出未知解的状态,转移方法就是状态转移方程。其实这道题还可以这么写:\(dp[i][j]\) 表示走到 \((i,j)\),已经取的值中能娶到的最大值,那么 \(dp[i][j]=max(dp[i-1][j-1],dp[i-1][j])+map[i][j]\)。最终答案就是 \(max(dp[N][j])\),在最下层中挑出解最大的一个,也就是反过来状态转移,这里不再赘述。
最长不下降子序列问题
https://blog.csdn.net/xr469786706/article/details/87901855
最长公共子序列问题
https://www.luogu.com.cn/problem/solution/P1439
参考资料
[1] 田翠华.算法设计与分析:冶金工业出版社,2007-08:106
[2] 叶金霞,白春章.信息技术 九年级:辽宁师范大学出版社,2008-07:113-114
[3] 百度百科:动态规划 https://baike.baidu.com/item/动态规划/529408?fr=aladdin
[4] OI-wiki: 记忆化搜索 https://oi-wiki.org/dp/memo/