A* search算法

今天，还是国庆和中秋双节的时间节点，一个天气不错的日子，孩子已经早早的睡觉了，玩了一整天，也不睡觉，累的实在扛不住了，勉强洗澡结束，倒床即睡着的节奏。。。

不多说题外话，进入正题。

什么是A*搜索算法呢？就用百科的解说吧：

A*算法，A*（A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法，也是解决许多搜索问题的有效算法。算法中的距离估算值与实际值越接近，最终搜索速度越快。

A*搜索的实际应用场景很多，但是大家最为熟悉的恐怕莫过于游戏了。典型的游戏就是穿越障碍寻宝，要求在最少的代价内找到宝贝，通常游戏中的代价，就是用最少的步骤实现宝贝的找寻。还有一种游戏场景是，给定入口地点，用最少的步骤走到指定的出口地点，中间有障碍物，每次只能在上下左右四个方向上走一步，且不能穿越障碍物。

就拿第二种游戏场景来解释A* search具体指的是什么内容吧。

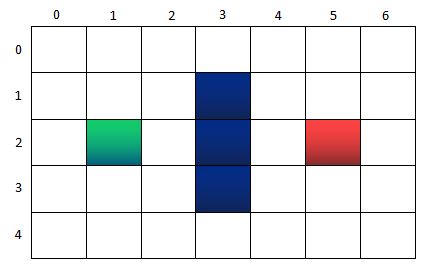
如上图所示，假设我们有一个7*5的迷宫方格，绿色的点表示起点，红色的点表示终点。中间三个蓝色的格子表示一堵墙，是障碍物。游戏的规则，是绿色的起点，每次只能向上下左右4个方向中移动一步，且不能穿越中间的墙，以最少的步骤到达红色的终点。

在解决这个问题之前，先要引入A*搜索算法的核心集合和公式：

核心集合：OpenList，CloseList

核心公式：F=G+H

其中，OpenList和CloseList用来存储格子点信息，OpenList表示可到达格子节点集合，CloseList表示已到达格子节点集合。

F=G+H表示对格子价值的评估，G表示从起点到当前点的代价；H表示从当前点到达终点的代价，指不考虑障碍物遮挡的情况下，这里，代价是指走的步数。至于F，就是对G和H的综合评估了，当然F越小，则从起点到达终点付出的代价就越小了。

就实际操作一下吧。还是上面的图，每个节点，用n(x,y)表示,x表示横坐标，y表示纵坐标，比如绿色的起点是n(1,2)：

第一步：把起点放入OpenList里面。

OpenList： n(1,2)

CloseList

第二步：找出OpenList中F值最小的方格，即唯一的方格n(1,2)作为当前方格，并把当前格移出OpenList，放入CloseList。表示这个格子已到达且验证过了。

OpenList

CloseList：n(1,2)

第三步：找出当前格上下左右所有可到达的格子，看它们是否在OpenList当中。如果不在，加入OpenList，计算出相应的G、H、F值，并把当前格子作为它们的“父节点”。

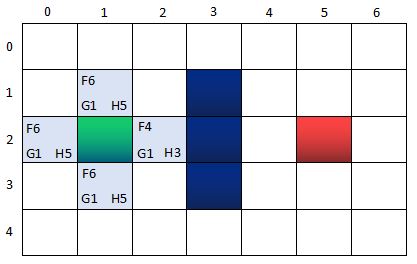
OpenList：n(0,2), n(1,1), n(2,2), n(1,3)

CloseList：n(1,2) 

其中，n(0,2), n(1,1), n(2,2), n(1,3)的父节点是n(1,2).所谓的父节点，表示当前的这几个节点n(0,2), n(1,1), n(2,2), n(1,3)都是从这个所谓的父节点出发得到的分支节点，父节点用作后续找出最短路径用的。

上述3步，是一次局部寻路的过程，我们需要不断的重复第二步第三步，最终找到到达终点的最短路径。

第二轮 ~ 第一步：找出OpenList中F值最小的方格，即方格n(2,2)作为当前方格，并把当前格移出OpenList，放入CloseList。代表这个格子已到达并检查过了。

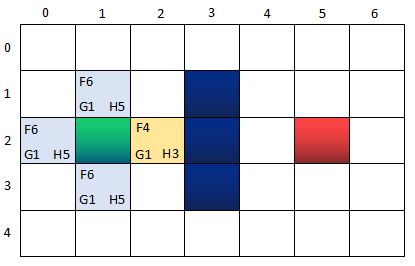
此时的两个核心集合的节点信息：

OpenList：n(0,2), n(1,1), n(1,3)

CloseList：n(1,2), n(2,2)

其中，n(0,2), n(1,1), n(1,3)的父节点是n(1,2)，n(2,2)的上一级节点（也可以称为父节点）是n(1,2).

第二轮 ~ 第二步：找出当前格上下左右所有可到达的格子，看它们是否在OpenList当中。如果不在，加入OpenList，计算出相应的G、H、F值，并把当前格子作为它们的“父节点”。

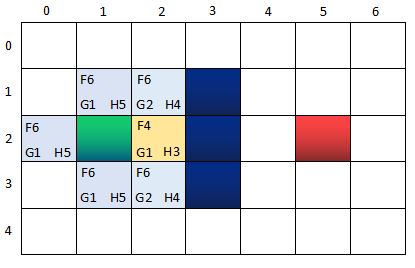
此时的两个核心集合的节点信息：

OpenList：n(0,2), n(1,1), n(1,3)；n(2,1), n(2,3)

CloseList：n(1,2) <-----n(2,2)

其中，n(0,2), n(1,1), n(1,3)的父节点是n(1,2)，而n(2,1), n(2,3)的父节点是n(2,2). CloseList中节点的指向关系，反映了寻路的路径过程。

为什么这一次OpenList只增加了两个新格子呢？因为n(3,2)是墙壁，自然不用考虑，而n(1,2)在CloseList当中，说明已经检查过了，也不用考虑。

第三轮 ~ 第一步：找出OpenList中F值最小的方格。由于这时候多个方格的F值相等，任意选择一个即可，比如n(2,3)作为当前方格，并把当前格移出OpenList，放入CloseList。代表这个格子已到达并检查过了。 

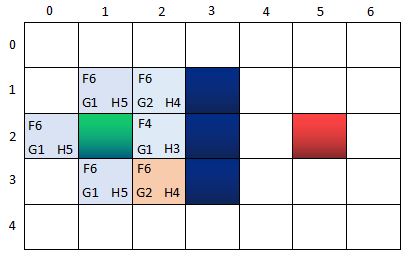
此时的两个核心集合的节点信息：

OpenList：n(0,2), n(1,1), n(1,3)；n(2,1) 

CloseList：n(1,2) <-----n(2,2)<-----n(2,3)

其中，n(0,2), n(1,1), n(1,3)的父节点是n(1,2)，而n(2,1)的父节点是n(2,2)。CloseList中节点的指向关系，反映了寻路的路径过程。

第三轮 ~ 第二步：找出当前格上下左右所有可到达的格子，看它们是否在OpenList当中。如果不在，加入OpenList，计算出相应的G、H、F值，并把当前格子作为它们的“父节点”。

此时的两个核心集合的节点信息：

OpenList：n(0,2), n(1,1), n(1,3)；n(2,1) ；n(2,4)

CloseList：n(1,2) <-----n(2,2)<-----n(2,3)

其中，n(0,2), n(1,1), n(1,3)的父节点是n(1,2)，而n(2,1)的父节点是n(2,2)。n(2,4)的父节点是n(2,3). CloseList中节点的指向关系，反映了寻路的路径过程。

剩下的就是以前面的方式继续迭代，直到OpenList中出现终点方格为止。

实际的推理，就到这里，下面，将结合上述的推理理论，用java程序，加以实现。今天，先将伪代码附上，改天将具体的java实现代码贴上来。

public Node AStarSearch(Node start, Node end) {
    // 把起点加入openList  
    openList.add(start);
    //主循环，每一轮检查一个当前方格节点
    while (openList.size() > 0) {
        // 在OpenList中查找F值最小的节点作为当前方格节点
        Node current = findMinNode();
        // 当前方格节点从open list中移除
        openList.remove(current);
        // 当前方格节点进入closeList
        closeList.add(current);
        // 找到所有邻近节点
        List<Node> neighbors = findNeighbors(current);
        for (Node node : neighbors) {
            if (!openList.contains(node)) {
                //邻近节点不在openList中，标记父亲、G、H、F，并放入openList
                markAndInvolve(current, end, node);
            }
        }
        //如果终点在OpenList中，直接返回终点格子
        if (find(openList, end) != null) {
            return find(openList, end);
        }
    }
    //OpenList用尽，仍然找不到终点，说明终点不可到达，返回空
    return null;
}

2017-10-13  11:28

过了几天了，今天终于回来补全未完成的最终实现代码逻辑，直接上代码：

package com.shihuc.nlp.astarsearch;

import java.io.File;
import java.io.FileNotFoundException;
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;

class Node {
    int x;  //当前节点的x坐标
    int y;  //当前节点的y坐标
    int px; //指向父节点的x坐标
    int py; //指向父节点的y坐标
}

public class Solution {    
    static List<Node> openList = new ArrayList<Node>();
    static List<Node> closeList = new ArrayList<Node>();    
    
    
    /**
     * @param args
     * @throws FileNotFoundException
     */
    public static void main(String[] args) throws FileNotFoundException {

        File file = new File("./src/com/shihuc/nlp/astarsearch/sample.txt");
        Scanner sc = new Scanner(file);
        int N = sc.nextInt();
        for (int n = 0; n < N; n++) {
            int Y = sc.nextInt();
            int X = sc.nextInt();
            int sx = sc.nextInt();
            int sy = sc.nextInt();
            int ex = sc.nextInt();
            int ey = sc.nextInt();
            Node start = new Node();
            start.x = sx; start.y = sy;
            Node end = new Node();
            end.x = ex; end.y = ey;
            int grid[][] = new int[X][Y];
            openList.clear();
            closeList.clear();
            for (int x = 0; x < X; x++) {
                for (int y = 0; y < Y; y++) {
                    grid[x][y] = sc.nextInt();
                }
            }
            Node ne = AStarSearch(start,end, grid);
            if(ne == null){
                System.out.println("No." + n + " Can not reach the end node");
            }else{
                add2Cl(ne);
                //printRawPath(n);
                printRealPath(n, start);
            }
        }
        if(sc != null){
            sc.close();
        }
    }
    
    /**
     * 打印当前节点以及其父节点的debug函数，查看父子节点关系
     * 
     * @author shihuc
     * @param idx
     */
    public static void printRawPath(int idx){
        System.out.println("No." + idx);
        for(Node p: closeList){             
            System.out.println("([" + p.x + "," + p.y + "][" + p.px + "," + p.py + "])"  );
        }
        System.out.println();
    }
    
    /**
     * 打印最终的路径信息的输出函数，起点节点用于输出结束判决
     * 
     * @author shihuc
     * @param start
     */
    public static void printRealPath(int idx, Node start){
        List<Node> path = new ArrayList<Node>();
        Node cn = closeList.get(closeList.size() - 1);
        Node temp = new Node();
        temp.x = cn.x;temp.y = cn.y;temp.px = cn.px;temp.py = cn.py;
        path.add(cn);
        do{
            for(int i=0; i<closeList.size(); i++){
                Node pn = closeList.get(i);
                if(temp.px == pn.x && temp.py == pn.y){                    
                    temp.px = pn.px;
                    temp.py = pn.py;
                    temp.x = pn.x;
                    temp.y = pn.y;
                    path.add(pn);
                    closeList.remove(pn);
                    break;
                }
            }    
        }while(!(temp.x == start.x && temp.y == start.y));
        System.out.print("No." + idx + " ");
        for(int i=path.size()-1 ; i >=0; i--){
            Node n = path.get(i);
            System.out.print("[" + n.x + "," + n.y + "]->");
        }
        System.out.println();
    }
    

    /**
     * A*搜索的完整算法实现。
     * 
     * @author shihuc
     * @param start 起点的坐标
     * @param end 目标点的坐标
     * @param grid 待搜索的网络
     * @return
     */
    public static Node AStarSearch(Node start, Node end, int grid[][]) {
        // 把起点加入 openList  
        add2Ol(start);
        // 主循环，每一轮检查一个当前方格节点
        while (openList.size() > 0) {
            // 在OpenList中查找 F值最小的节点作为当前方格节点
            Node current = findMinNode(start,end);
            // 当前方格节点从openList中移除
            remove4Ol(current);
            // 当前方格节点进入 close list
            add2Cl(current);
            // 找到所有邻近节点
            List<Node> neighbors = findNeighbors(current, grid);
            for (Node node : neighbors) {
                if (openListMarkedNode(node) == null) {
                    //邻近节点不在OpenList中,标记父节点，并放入OpenList
                    markAndInvolve(current, node);                    
                }
            }
            // 如果终点在OpenList中，直接返回终点格子
            Node last = findInOpenList(end);
            if ( last != null) {                
                return last;
            }
        }
        // OpenList用尽，仍然找不到终点，说明终点不可到达，返回空
        return null;
    }
        
    /**
     * 向openList添加节点。若节点已经存在，则不添加。
     * 
     * @author shihuc
     * @param n 待添加的节点
     */
    private static void add2Ol(Node n){
        if(openListMarkedNode(n) == null){
            openList.add(n);
        }
    }
    
    /**
     * 向closeList添加节点信息。若节点已经存在，则不添加。
     * 
     * @author shihuc
     * @param n
     */
    private static void add2Cl(Node n){        
        for(Node pn: closeList){            
            if(pn.x == n.x && pn.y == n.y){                
                return;
            }
        }        
        closeList.add(n);
    }
    
    /**
     * 从openList中删除指定的节点。通过坐标信息定位指定节点。
     * 
     * @author shihuc
     * @param n
     */
    private static void remove4Ol(Node n){
        for(Node ne:openList){
            if(ne.x == n.x && ne.y == n.y){
                openList.remove(ne);
                return;
            }
        }
    }
    
    /**
     * openlist中若有已经标记的指定节点，则返回该节点，否则返回null节点。
     * 
     * @author shihuc
     * @param n
     * @return
     */
    private static Node openListMarkedNode(Node n){
        for(Node ne: openList){
            if(ne.x == n.x && ne.y == n.y){
                return ne;
            }
        }
        return null;
    }
    
    /**
     * 从closeList检查是否存在指定的节点。
     * 
     * @author shihuc
     * @param n
     * @return
     */
    private static boolean isInCloseList(Node n){
        for(Node pn: closeList){            
            if(pn.x == n.x && pn.y == n.y){
                return true;
            }
        }
        return false;
    }
        
    /**
     * 利用类似勾股定理的方式计算H值以及G值。
     * 
     * @author shihuc
     * @param x
     * @param y
     * @return
     */
    private static int gouguLaw(int x, int y){
        return x*x + y*y;
    }
    
    /**
     * 在openList中查找F=G+H的值最小的节点。
     * 
     * @author shihuc
     * @param start
     * @param end
     * @return
     */
    public static Node findMinNode(Node start, Node end){
        int fMin = 0;
        int sx = start.x, sy = start.y;
        int ex = end.x, ey = end.y;
        Node nm = new Node();
        Node n0 = openList.get(0);
        nm.x = n0.x;nm.y = n0.y;
        fMin = gouguLaw(n0.x - sx, n0.y - sy) + gouguLaw(n0.x - ex, n0.y - ey);
        for(int i=1; i<openList.size(); i++){
            Node n = openList.get(i); 
            int g = gouguLaw(n.x - sx, n.y - sy);
            int h = gouguLaw(n.x - ex, n.y - ey);            
            if(fMin > g+h){
                nm.x = n.x;
                nm.y = n.y;
                nm.px = n.px;
                nm.py = n.py;
                fMin = g+h;                
            }
        }
        return nm;
    }
    
    /**
     * 以当前节点为中心，查找没有验证过（不在closeList中）的上下左右邻居节点。
     * 
     * @author shihuc
     * @param current
     * @param grid
     * @return
     */
    public static List<Node> findNeighbors(Node current, int grid[][]){
        int x = current.x;
        int y = current.y;
        
        int Y = grid.length;
        int X = grid[0].length;
        
        List<Node> neigs = new ArrayList<Node>();
        if(x - 1 >= 0 && grid[y][x - 1] != 1){
            Node nu = new Node();
            nu.x = x - 1;
            nu.y = y;    
            if(!isInCloseList(nu)){
                neigs.add(nu);            
            }
        }
        if(x + 1 < X && grid[y][x+1] != 1){
            Node nu =  new Node();
            nu.x = x + 1;
            nu.y = y;
            if(!isInCloseList(nu)){
                neigs.add(nu);            
            }
        }
        if(y - 1 >= 0  && grid[y - 1][x] != 1){
            Node nu =  new Node();
            nu.x = x;
            nu.y = y - 1;
            if(!isInCloseList(nu)){
                neigs.add(nu);            
            }
        }
        if(y + 1 < Y && grid[y + 1][x] != 1){
            Node nu =  new Node();
            nu.x = x;
            nu.y = y + 1;
            if(!isInCloseList(nu)){
                neigs.add(nu);            
            }
        }    
        return neigs;        
    }
    
    /**
     * 检查指定节点是否在openList中。
     * 
     * @author shihuc
     * @param ed
     * @return
     */
    public static Node findInOpenList(Node ed){
        return openListMarkedNode(ed);            
    }
    
    /**
     * 这个函数非常重要，标记当前节点的邻居节点的父亲节点为当前节点，这个标记关系，用于后续输出A*搜索的最终路径
     * 
     * @author shihuc
     * @param current
     * @param n
     */
    public static void markAndInvolve(Node current, Node n){
        n.px = current.x;
        n.py = current.y;
        openList.add(n);
    }
}

测试用到的数据样本（sample.txt内容）：

3
7 5
1 2 5 2
0 0 0 0 0 0 0
0 0 0 1 0 0 0
0 0 0 1 0 0 0
0 0 0 1 0 0 0
0 0 0 0 0 0 0
7 5
1 2 5 2
0 0 0 1 0 0 0
0 0 0 1 0 0 0
0 0 0 1 0 0 0
0 0 0 1 0 0 0
0 0 0 1 0 0 0
20 15
1 1 19 14
0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1 1
0 0 1 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1
0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0 1
0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 1
0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0
0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
0 1 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0
0 0 0 0 1 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0
0 1 0 0 0 0 1 0 0 0 0 0 0 1 0 1 0 0 0 1
0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0

最终的数据测试结果：

No.0 [1,2]->[2,2]->[2,1]->[2,0]->[3,0]->[4,0]->[4,1]->[4,2]->[5,2]->
No.1 Can not reach the end node
No.2 [1,1]->[1,2]->[2,2]->[3,2]->[4,2]->[4,3]->[4,4]->[5,4]->[6,4]->[7,4]->[7,5]->[7,6]->[8,6]->[9,6]->[9,7]->[10,7]->[11,7]->[11,8]->[11,9]->[12,9]->[12,10]->[13,10]->[13,11]->[14,11]->[14,12]->[15,12]->[16,12]->[16,13]->[16,14]->[17,14]->[18,14]->[19,14]->

上述算法，场景比较简单，当前节点的上下左右四个方向，有的要求8个方向的，甚至障碍物有其他的要求的。都离不开这里的最要思想，F=G+H.

欢迎探讨，欢迎评论以及转帖，请注明出处！