关于B+树数据结构
①InnoDB存储引擎支持两种常见的索引(B+树和哈希)。
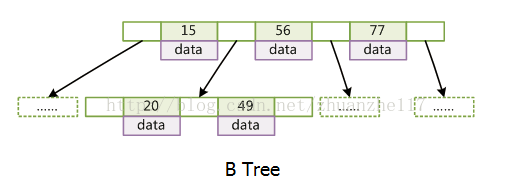
B+树中的B意思是平衡(Balance),B+树是由B树(即B-tree)演变过来的多叉平衡树。
同时,B+树索引并不能找到一个给定键值的具体行。B+树索引只能找到的是被查找数据行所在的页。然后数据库通过把页读入内存,再在内存中进行查找,最后得到查找的数据。
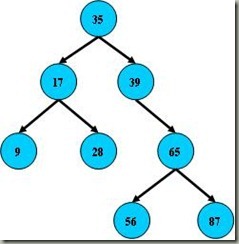
先说一下平衡二叉树:
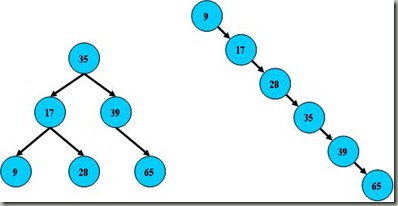
这是一幅平衡二叉树,左子树的值总是小于根的值,右子树的值总是大于根的键值,因此可以通过中序遍历(以递归的方式按照左中右的顺序来访问子树),因此遍历以后得到的输出是9、17、28、35、39、56、65、87。这样,如果要查找键值为28的记录,先找到根,然后发现根大于28,找左子树,发现左子树的根17小于28,再找下一层右子树,然后找到28。通过了3次查找找到了需要找的节点。但是如果二叉树节点分布非常不均匀,就像第二张图那样,那么二叉搜索树就会完全退化成线性表。因此如果想要最大性能地构造一个二叉查找树,需要这颗二叉查找树是平衡的,平衡二叉树对于查找的性能是比较高的,但是不是最高的,只是接近最高的性能。要达到最好的性能,需要建立一颗最优二叉树,但是最优二叉树的建立和维护需要大量的操作,因此用平衡二叉树就比较好。同时,平衡二叉树多用于内存结构对象中,因此维护他的开销相对较小。
②为什么使用B+树呢?
虽然二叉查找树和平衡二叉树都能够实现较快的数据查找,但是,由于数据库的内容是存在于磁盘上,而磁盘IO与内存IO相比,比内存IO慢了10^5~10^6倍,为了减少磁盘IO,提高检索速度,因而才用了B+树(一种多路平衡查找树)这种数据结构。
③什么是B+树,其特性是什么
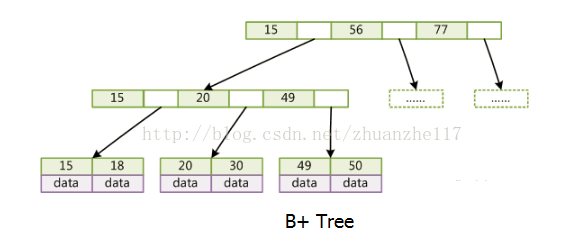
B+树的概念还是过于复杂,直接上图比较合适:
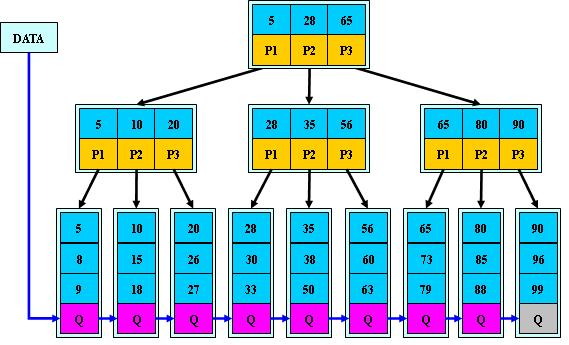
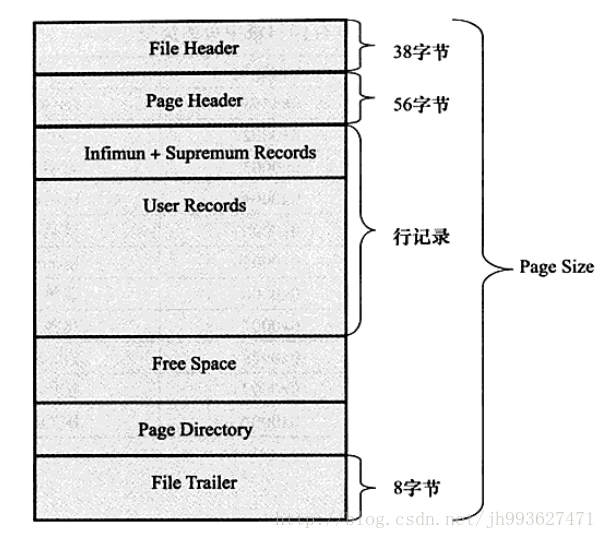
从图可以看出,所有记录的节点都在叶节点中,并且是顺序存放的,如果我们从最左边的节点开始遍历,可以得到的所有键值的顺序是:1、2、3、4、5、6、7。
在B+树中,所有记录节点都是按照键值的大小顺序存放在同一层的叶节点中,各个叶子节点通过指针进行连接。由于一个节点中存放了多条的数据(1页),那么检索的时候,进行的磁盘IO次数将会少掉很多。这是用b+树而不用二叉树的原因。
在B+树插入的时候,为了保持平衡,对于新插入的键值可能需要做大量的拆分页操作,而B+树主要用于磁盘,因此页的拆分意味着磁盘操作,因此应该在可能的情况下尽量减少页的拆分。设置主键自增就是为了减少结点的拆分页。
关于索引
InnoDB存储引擎使用聚集索引,实际的数据行和相关键值保存在一块。因而,在InnoDB中要使用索引访问数据始终需要两次查找,而不是一次。因为索引叶子节点中存储的不是行的物理位置,而是主键的值。即:二次索引-->主键-->数据的叶子-->通过数据叶字节点中的page directory找到数据行。
因为每一张InnoDB的表都会有一个主键索引,但是如果没有显式指定怎么办?如果没有手工去指定主键索引的话,那么,InnoDB引擎会指派一个unique的列作为主键,如果没有unique的字段的话,那么便会自动生成一个隐含的列作为主键。
所以,在在InnoDB的设计中,应该尽可能的使用一个与业务无关auto_increment的自增主键,而不要去使用uuid之类的随机(无序)的聚集键。同时,由于所有的索引都使用主键的索引,如果主键索引过长,也会使辅助索引相应的变大。
聚集索引的存储并不是物理上的连续,而是逻辑上连续的。一方面,页通过双向链表连接,页按照主键的顺序排列;另一方面,每个页中的记录也是通过双向链表进行维护,物理存储上可以同样不按照主键存储。
为什么选用B+树?
磁道就是以盘片为中心划分出来的一系列同心环。磁道又划分为一个个小段,叫扇区,是磁盘的最小存储单元。磁盘读取时,磁盘的控制电路会将数据逻辑地址解析出物理地址,即哪个磁道哪个扇区。于是磁头需要前后移动到对应的磁道,消耗的时间叫寻道时间,然后磁盘旋转将对应的扇区转到磁头下,消耗的时间叫旋转时间。
一般来说,索引本身也很大,不可能全部存储在内存中,因此索引往往以索引文件的形式存储的磁盘上。这样的话,索引查找过程中就要产生磁盘I/O消耗,所以评价索引的优劣最重要的指标就是在查找过程中磁盘I/O操作次数的复杂度。换句话说,索引的结构组织要尽量减少查找过程中磁盘I/O的存取次数。
为了尽量减少I/O操作,磁盘读取每次都会预读,大小通常为页的整数倍。即使只需要读取一个字节,磁盘也会读取一页的数据(通常为4K)放入内存,内存与磁盘以页为单位交换数据。因为局部性原理认为,通常一个数据被用到,其附近的数据也会立马被用到。
B树:如果一次检索需要访问4个节点,数据库系统设计者利用磁盘预读原理,把节点的大小设计为一个页,那读取一个节点只需要一次I/O操作,完成这次检索操作,最多需要3次I/O(根节点常驻内存)。数据记录越小,每个节点存放的数据就越多,树的高度也就越小,I/O操作就少了,检索效率也就上去了。
B+树:非叶子节点只存key,大大滴减少了非叶节点的大小,那么每个非叶节点就可以存放更多的记录,树更矮了,I/O操作更少了。所以B+Tree拥有更好的性能。