机器学习

梯度下降求解逻辑回归 - 算法实现

相关模块 - 三大件

#三大件
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

数据集 - 大学录取

我们将建立一个逻辑回归模型来预测一个学生是否被大学录取。

假设你是一个大学系的管理员，你想根据两次考试的结果来决定每个申请人的录取机会。

你有以前的申请人的历史数据，你可以用它作为逻辑回归的训练集。

对于每一个培训例子，你有两个考试的申请人的分数和录取决定。

为了做到这一点，我们将建立一个分类模型，根据考试成绩估计入学概率。

import os
path = 'data' + os.sep + 'LogiReg_data.txt'
pdData = pd.read_csv(path, header=None, names=['Exam 1', 'Exam 2', 'Admitted'])
pdData.head()
pdData.shape   #(100, 3) 数据维度 100 行, 3列

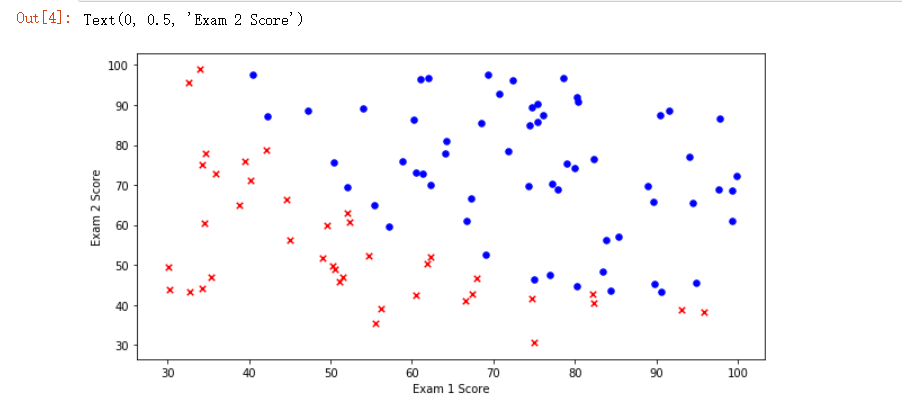
图形展示 - 散点图

positive = pdData[pdData['Admitted'] == 1] # returns the subset of rows such Admitted = 1, i.e. the set of *positive* examples
negative = pdData[pdData['Admitted'] == 0] # returns the subset of rows such Admitted = 0, i.e. the set of *negative* examples

fig, ax = plt.subplots(figsize=(10,5))
ax.scatter(positive['Exam 1'], positive['Exam 2'], s=30, c='b', marker='o', label='Admitted')
ax.scatter(negative['Exam 1'], negative['Exam 2'], s=30, c='r', marker='x', label='Not Admitted')
ax.legend() # 展示图形标识
ax.set_xlabel('Exam 1 Score') # x 标识
ax.set_ylabel('Exam 2 Score') # y 标识

 

逻辑回归 - 实现算法

▒ 目标

 ▨ 建立分类器 

 ▨ 求解三个参数 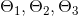 - 分别表示 成绩一, 成绩二以及偏置项的参数 

▒ 阈值

  ▨ 设定阈值来标识分类的结果, 此处设置为 0.5 

  ▨ > 0.5  标识通过, < 0.5 标识未通过

▒ 所需模块

  ▨ sigmoid : 映射到概率的函数

  ▨ model : 返回预测结果值

  ▨ cost : 根据参数计算损失

  ▨ gradient : 计算每个参数的梯度方向

  ▨ descent : 进行参数更新

  ▨ accuracy: 计算精度

▒ sigmoid 函数实现

  ▨  公式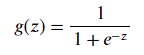 　　 

  ▨  Python 实现 　　  def sigmoid(z): return 1 / (1 + np.exp(-z)) 

  ▨ 画图展示 

nums = np.arange(-10, 10, step=1) #creates a vector containing 20 equally spaced values from -10 to 10
fig, ax = plt.subplots(figsize=(12,4))
ax.plot(nums, sigmoid(nums), 'r')

 

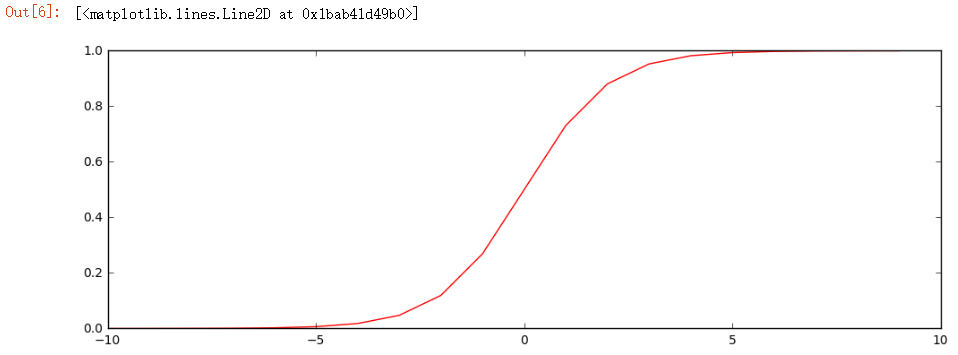
  ▨ 值域 

    

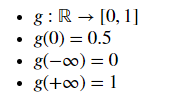
▒  model 函数 - 预测函数实现 

  ▨ 数学公式  　　 

  ▨ Python 实现 

def model(X, theta):
    
    return sigmoid(np.dot(X, theta.T))

▒  构造数据集

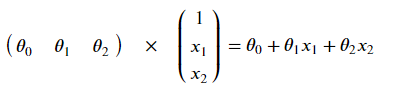
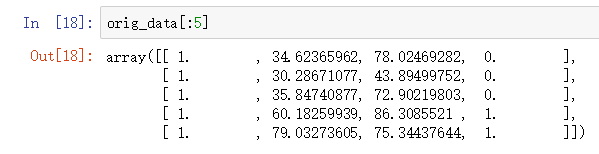
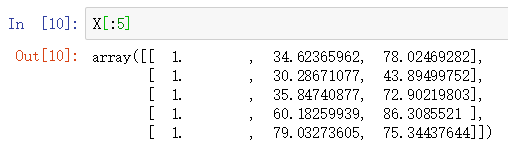
 ▨ 加一行 -  数据集要进行偏置项的处理 ( 加一列全1的数据 )

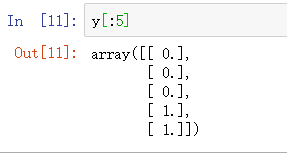
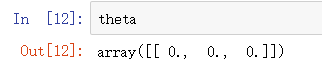
pdData.insert(0, 'Ones', 1) # 偏置项参数的处理


# set X (training data/训练数据) and y (target variable/变量参数)
orig_data = pdData.as_matrix() # 转换为 数组形式
cols = orig_data.shape[1]
X = orig_data[:,0:cols-1]
y = orig_data[:,cols-1:cols]

# convert to numpy arrays and initalize the parameter array theta
#X = np.matrix(X.values)
#y = np.matrix(data.iloc[:,3:4].values) #np.array(y.values)
theta = np.zeros([1, 3])  # 参数占位, 先用 0 填充

 

▒  损失函数

  ▨ 数学公式 

　　

　　将对数似然函数去负号 -　　 

　　求平均损失 - 　　

　　这块如果忘了怎么回事可以在这里进行查阅 点击这里跳转公式篇

   ▨  Python 实现 

def cost(X, y, theta):
    left = np.multiply(-y, np.log(model(X, theta)))
    right = np.multiply(1 - y, np.log(1 - model(X, theta))) 
    return np.sum(left - right) / (len(X))

  X, y  表示两个特征值, 传入  theta  表示参数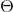  

 np.multiply  乘法计算, 将式子分为左右查分

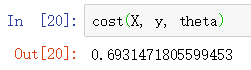
   ▨  计算 cost 值

▒  计算梯度

   ▨  数学公式 - 进行求导计算后, 将最终结果转换为 python 实现

　　　　

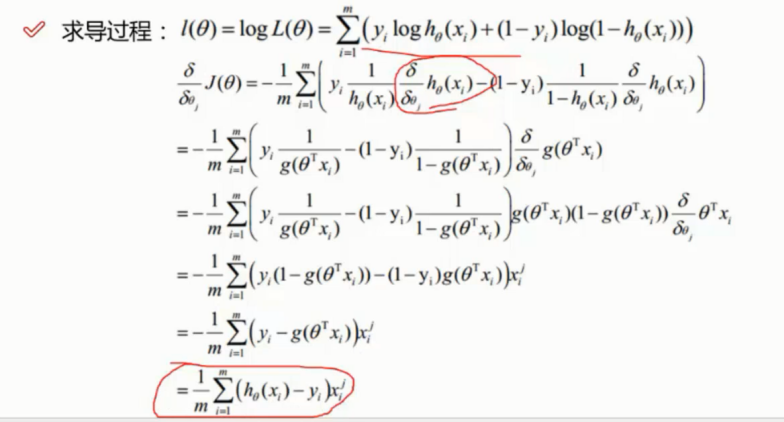
    ▨  Python 实现

def gradient(X, y, theta):
    grad = np.zeros(theta.shape) # 因为会有三个结果, 因此这里进行预先的占位
    error = (model(X, theta)- y).ravel() # h0(xi)-yi 象形... 这里吧前面的m分之一的那个负号移到了这里来去除负号
    for j in range(len(theta.ravel())): # 求三次
        term = np.multiply(error, X[:,j]) # : 表示所有的行, j 表示第 j 列
        grad[0, j] = np.sum(term) / len(X)
    
    return grad

 　   这里有三个 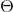 , 那么应该也是计算出来三个值, 因此这里进行了三次的循环

　　每次的循环针对要处理的那一列进行操作

▒  停止策略

STOP_ITER = 0 # 根据迭代次数, 达到迭代次数及停止
STOP_COST = 1 # 根据损失, 损失差异较小及停止
STOP_GRAD = 2 # 根据梯度, 梯度变化较小则停止

def stopCriterion(type, value, threshold):
    #设定三种不同的停止策略
    if type == STOP_ITER:        return value > threshold
    elif type == STOP_COST:      return abs(value[-1]-value[-2]) < threshold
    elif type == STOP_GRAD:      return np.linalg.norm(value) < threshold

▒  洗牌

import numpy.random
#洗牌
def shuffleData(data):
    np.random.shuffle(data)
    cols = data.shape[1]
    X = data[:, 0:cols-1]
    y = data[:, cols-1:]
    return X, y

初始的数据集很大可能性是有做过排序的, 因此需要进行洗牌

然后重新生成我们需要的数据

▒  核心操作函数 

import time

def descent(data, theta, batchSize, stopType, thresh, alpha):
    #梯度下降求解
    
    init_time = time.time()
    i = 0 # 迭代次数
    k = 0 # batch
    X, y = shuffleData(data)
    grad = np.zeros(theta.shape) # 计算的梯度
    costs = [cost(X, y, theta)] # 损失值

    
    while True:
        grad = gradient(X[k:k+batchSize], y[k:k+batchSize], theta) 
        k += batchSize #取batch数量个数据
        if k >= n: 
            k = 0 
            X, y = shuffleData(data) #重新洗牌
        theta = theta - alpha*grad # 参数更新
        costs.append(cost(X, y, theta)) # 计算新的损失
        i += 1 

        if stopType == STOP_ITER:       value = i
        elif stopType == STOP_COST:     value = costs
        elif stopType == STOP_GRAD:     value = grad
        if stopCriterion(stopType, value, thresh): break
    
    return theta, i-1, costs, grad, time.time() - init_time

    ▨  参数详解

•  data  -  数据
•  theta  - 参数
•  batchSize  这里的指定及选择下降方式
  • 如果指定为 1 则表示随机, 指定为总样本数则表示批量, 指定 1-总数 之间则表示小批量
• stopType  - 停止策略
  • 迭代次数 - 达到指定次数停止
  • 损失 - 损失较小停止
  • 梯度 - 梯度较小停止
• thresh  -  策略对应的阈值,
  • 比如选择 迭代次数停止策略, 则此值表示迭代次数的上限, 
• alpha  - 学习率 ( 就那个 0.01 ~ 0.0....1 的那个)

▒  辅助工具函数

def runExpe(data, theta, batchSize, stopType, thresh, alpha):
    #import pdb; pdb.set_trace();
    theta, iter, costs, grad, dur = descent(data, theta, batchSize, stopType, thresh, alpha)  # 这是最核心的代码

    name = "Original" if (data[:,1]>2).sum() > 1 else "Scaled"
    name += " data - learning rate: {} - ".format(alpha)
    # 根据传入参数选择下降方式 
    if batchSize==n: strDescType = "Gradient"  #  批量
    elif batchSize==1:  strDescType = "Stochastic"  # 随机 
    else: strDescType = "Mini-batch ({})".format(batchSize) # 小批量
    name += strDescType + " descent - Stop: "
    # 根据 停止方式进行选择处理生成 name 
    if stopType == STOP_ITER: strStop = "{} iterations".format(thresh)
    elif stopType == STOP_COST: strStop = "costs change < {}".format(thresh)
    else: strStop = "gradient norm < {}".format(thresh)
    name += strStop
    print ("***{}
Theta: {} - Iter: {} - Last cost: {:03.2f} - Duration: {:03.2f}s".format(
        name, theta, iter, costs[-1], dur))
    # 画图 
    fig, ax = plt.subplots(figsize=(12,4))
    ax.plot(np.arange(len(costs)), costs, 'r')
    ax.set_xlabel('Iterations')
    ax.set_ylabel('Cost')
    ax.set_title(name.upper() + ' - Error vs. Iteration')
    return theta

此函数进行画图的一些名字的显示以及图形进行的简单的功能封装函数

可以理解为一个工具函数, 自动根据参数选择画图的某些调节比如标题等

逻辑回归 - 算法计算

停止策略比较 

▒  批量下降 - 迭代次数停止策略

n=100
runExpe(orig_data, theta, n, STOP_ITER, thresh=5000, alpha=0.000001)

    ▨  参数详解

• 这里 设置 100 为样本的总数据量, 因此这是个批量下降方式的计算
• 停止策略是基于迭代次数进行判断
•  thresh  5000 表示迭代次数
• 学习率的设置为 0.00001 非常的小,  

    ▨  测试结果

　　

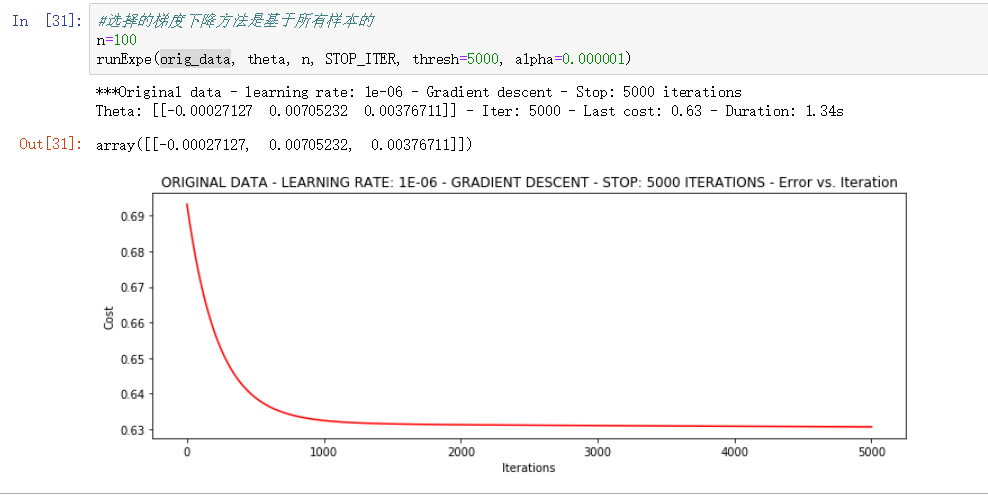
    ▨  结果详解

　　1.34s 完成了全部的 5000次 迭代, 最终的结果的为 0.63 左右

▒  批量下降 - 损失值停止策略

runExpe(orig_data, theta, n, STOP_COST, thresh=0.000001, alpha=0.001)

    ▨  参数详解

• 这里 依旧设置 100 为样本的总数据量, 依旧为批量下降方式的计算
• 停止策略是基于损失值进行判断
•  thresh  设置为如果损失小于 0.000001 的时候则停止
• 学习率的设置为 0.00001 非常的小

    ▨  测试结果

 

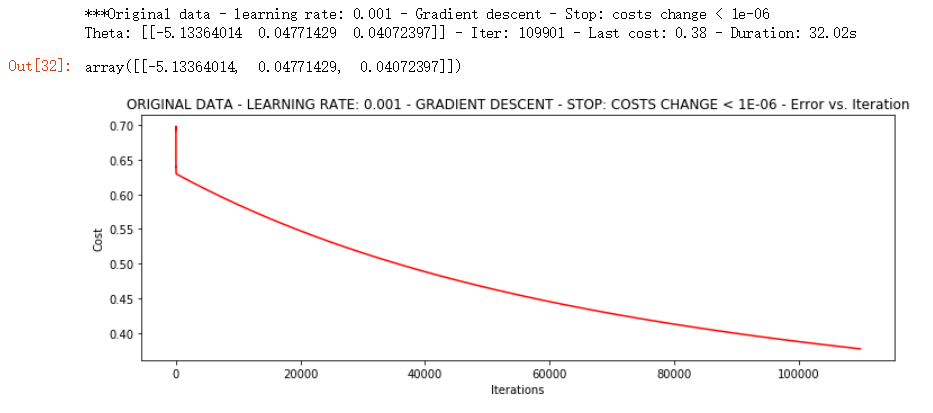
    ▨  结果详解

　　可见测试用了 32.02s才完成, 达到损失值这么小的时候用了 100000次以上的迭代次数, 但是结果也达到了 0.4 以下

　　比上一轮的结果要优秀很多

▒  批量下降 - 梯度值停止策略

runExpe(orig_data, theta, n, STOP_GRAD, thresh=0.05, alpha=0.001)

    ▨  参数详解

• 这里 依旧设置 100 为样本的总数据量, 依旧为批量下降方式的计算
• 停止策略是基于梯度值变化进行判断
•  thresh  设置 0.05 表示梯度变化 
• 学习率的设置为 0.00001 非常的小

    ▨  测试结果

 

    ▨  结果详解

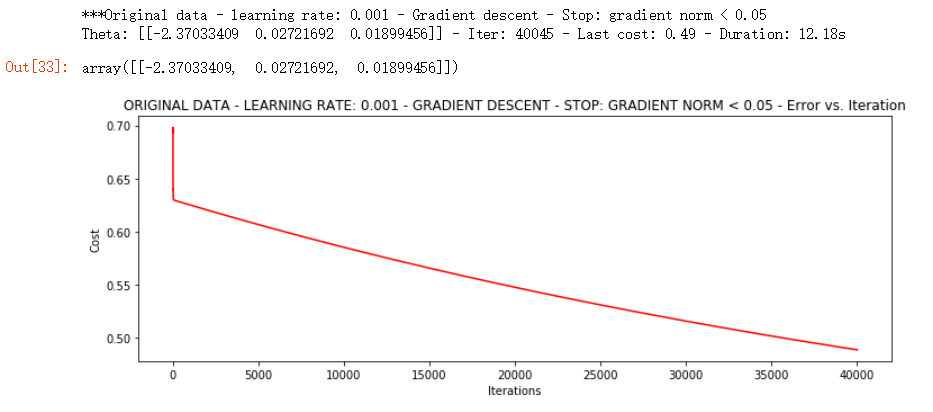
　　可见测试用了12.18s 才完成, 达到损失值这么小的时候用了40000 次以上的迭代次数, 但是结果也达到了 0.5 以下

　　由迭代次数也可以看出比不过 12w 次的结果, 因此最终的收敛在 0.50 左右无法比过 0.4 的上轮结果

▒  总结

通过以上的三轮比较可以看出. 迭代次数越多得到的收敛结果越好, 而且某些方式还会存在误判的

比如此图中从2000开始后面就趋于平缓, 实际上并没有能够完全收敛到极限

梯度下降比较

▒  随机下降 

　　

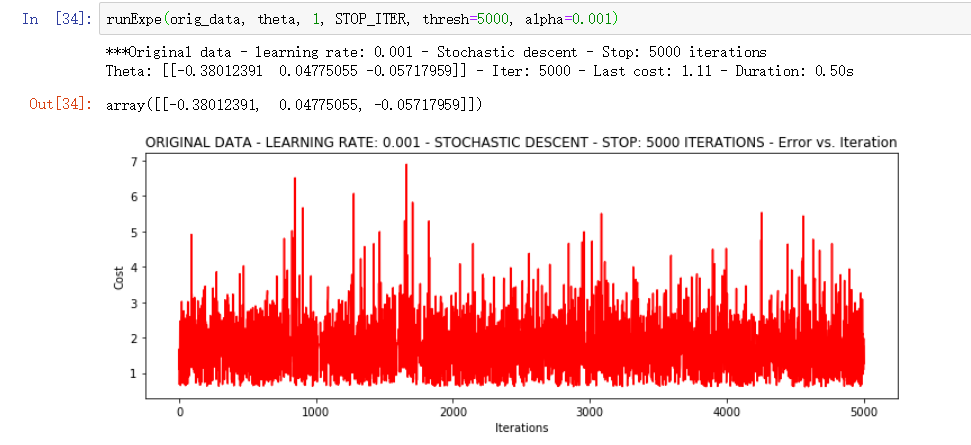
 　　可以看出随机下降的5000此迭代的结果非常不稳定, 损失值忽上忽下, 基本上完全没办法收敛的, 当然时间很快啊就只需要 0.50s 

　　 当然这么理想的成绩也是因为学习率的问题, 学习率进行调整后再试一次

    ▨  调整学习率

　　

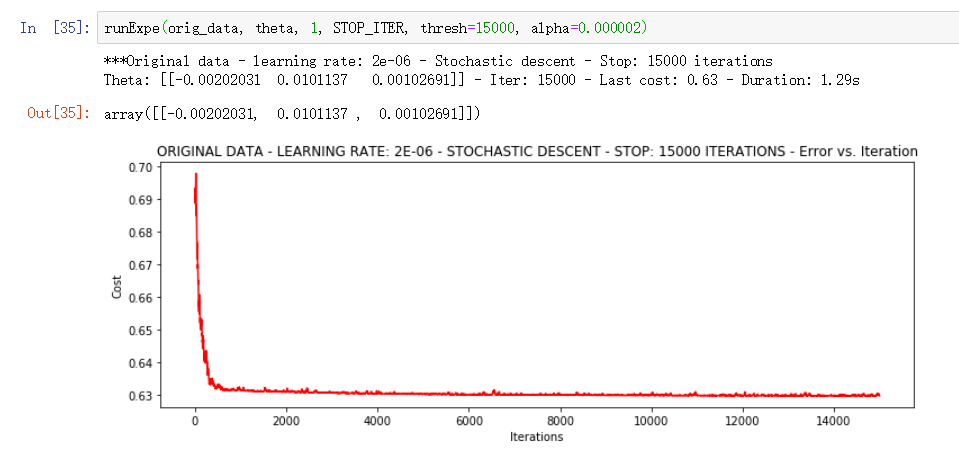
 在调整了学习率以及增大了迭代次数之后, 损失值确实进行了一定程度的收敛, 但是收敛到 0.63 左右不算很理想的成绩

▒  小批量下降 　　

　　

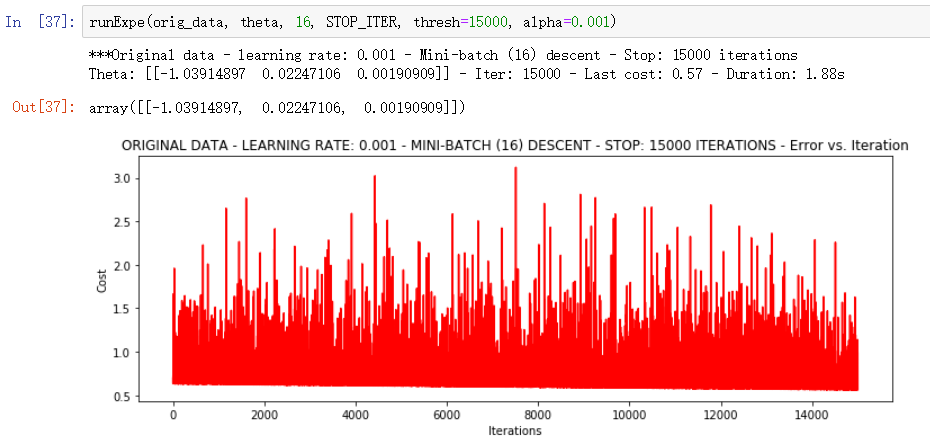
 　　小批量下降, 每次使用 16个样本数据进行 15000次学习率为 0.001 的迭代, 结果无收敛, 耗时 1.88s

　　 进一步优化的话可以继续调整学习率, 也可以换另一种方案 ---- 数据标准化

    ▨  数据标准化

 　　将数据按其属性(按列进行)减去其均值，然后除以其方差。

　　最后得到的结果是，对每个属性/每列来说所有数据都聚集在0附近，方差值为1

from sklearn import preprocessing as pp

scaled_data = orig_data.copy()
scaled_data[:, 1:3] = pp.scale(orig_data[:, 1:3])

runExpe(scaled_data, theta, n, STOP_ITER, thresh=5000, alpha=0.001)

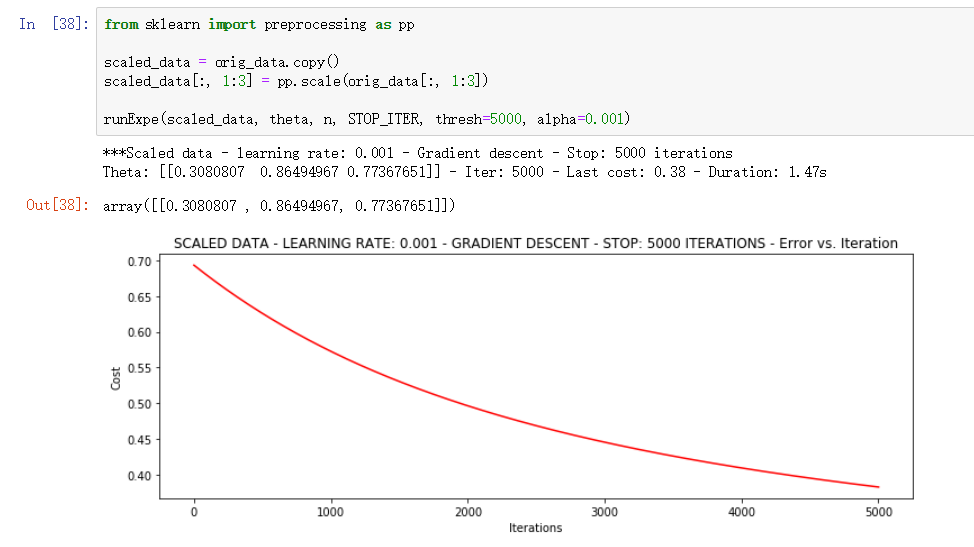
　　标准化处理后数据进行了收敛, 且收敛在 0.4以下是较为优秀的结果了

    ▨ 对比

 

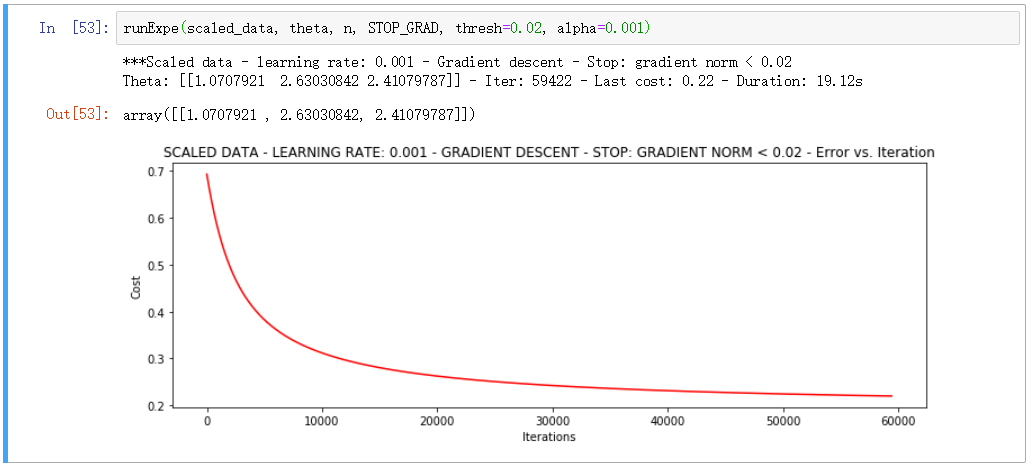
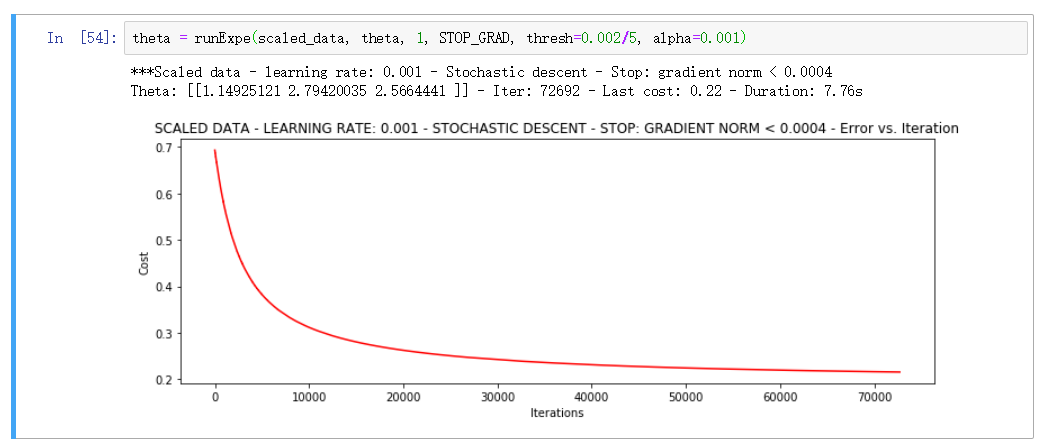
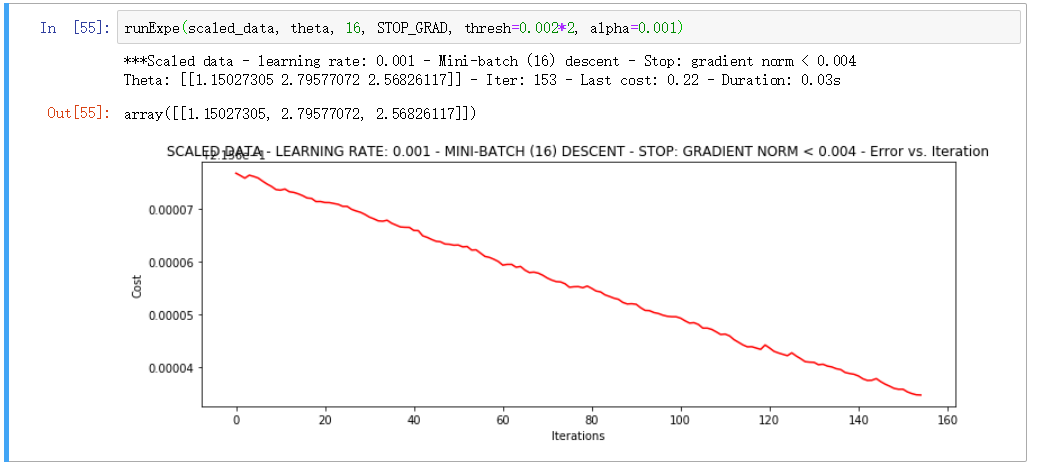
▒  总结

　　在收敛效果不佳的时候, 先改数据再改模型是一个基本的套路

　　对比三种下降方式, 综合选择小批量为最优选择

▒  精度计算

#设定阈值
def predict(X, theta):
    return [1 if x >= 0.5 else 0 for x in model(X, theta)]

首先将阈值进行转换为 分类

scaled_X = scaled_data[:, :3]
y = scaled_data[:, 3]
predictions = predict(scaled_X, theta)
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)]
accuracy = (sum(map(int, correct)) % len(correct))
print ('accuracy = {0}%'.format(accuracy))

最终输出精度

accuracy = 89%