0、缘起
一直ym传说中的kmp算法能以最坏线性的时间复杂度搞定字符串匹配,
开始动手看才知道kmp中的K居然是Donald.E.Knuth,《计算机程序设计艺术》的作者。
好吧,继续ym……
1、传统的字符串匹配算法
/*
* 从s中第sIndex位置开始匹配p
* 若匹配成功,返回s中模式串p的起始index
* 若匹配失败,返回-1
*/
int index(const std::string &s, const std::string &p, const int sIndex = 0)
{
int i = sIndex, j = 0;
if (s.length() < 1 || p.length() < 1 || sIndex < 0)
{
return -1;
}
while (i != s.length() && j != p.length())
{
if (s[i] == p[j])
{
++i;
++j;
}
else
{
i = i - j + 1;
j = 0;
}
}
return j == p.length() ? i - j: -1;
}
2、传统字符串匹配算法的性能问题
用模式串P去匹配字符串S,在i=6,j=4时发生失配:
i=6
S: a b a b c a d c a c b a b
P: a b c a c
j=4
此时,按照传统算法,应当将P的第 1 个字符 a(j=0) 滑动到与S中第4个字符 b(i=3) 对齐再进行匹配:
i=3
S: a b a b c a a d a c b a b
P: a b c a c
j=0
这个过程中,对字符串S的访问发生了“回朔”(从 i=6 移回到 i=3)。
我们不希望发生这样的回朔,而是试图通过尽可能的“向右滑动”模式串P,让P中index为 j 的字符对齐到S中 i=5 的字符,然后试图匹配S中 i=6 的字符与P中index为 j+1 的字符。
在这个测试用例中,我们直接将P向右滑动3个字符,使S中 i=5 的字符与P中 j=0 的字符对齐,再匹配S中 i=6 的字符与P中 j=1 的字符。
i=6
S: a b a b c a d c a c b a b
P: a b c a c
j=0
3、kmp算法的一般性讨论
下面讨论在一般性的情况下,如何实现在“不回朔”访问S、仅依靠“滑动”P的前提下实现字符串匹配,即“kmp算法”。
i=6
S: a b a b c a d c a c b a b
P: a b c a c
k=1
i=6
S: a b a b c a d c a c b a b
P: a b c a c
j=4
对于任意的S和P,当S中index为 i 的字符和P中index为 j 的字符失配时,我们假定应当滑动P使其index为 k 的字符与S中index为 i 的字符“对齐”并继续比较。
那么,这个 k 是多少?
我们知道,所谓的对齐,就是要让S和P满足以下条件(上图中的蓝色字符):
 ……(1)
……(1)
另一方面,在失配时我们已经有了一些部分匹配结果(上图中的绿色字符):
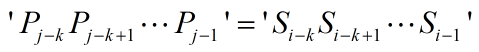 ……(2)
……(2)
由(1)、(2)可以得到:
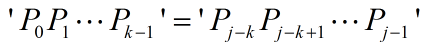 ……(3)
……(3)
即如下图所示效果:

定义next[j]=k,k表示当模式串P中index为 j 的字符与主串S中index为 i 的字符发生失配时,应将P中index为 k 的字符继续与主串S中index为 i 的字符比较。
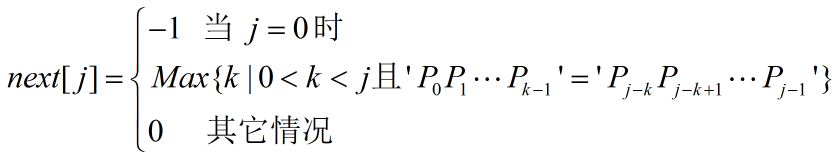 ……(4)
……(4)
按上述定义给出next数组的一个例子:
j 0 1 2 3 4 5 6 7
P a b a a b c a c
next[j] -1 0 0 1 1 2 0 1
在已知next数组的前提下,字符串匹配的步骤如下:
i 和 j 分别表示在主串S和模式串P中当前正待比较的字符的index,i 的初始值为sIndex,j 的初始值为0。
在匹配过程中的每一次循环,若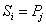 ,i 和 j 分别增 1,
,i 和 j 分别增 1,
else,j 退回到 next[j]的位置,此时下一次循环是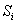 与
与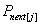 相比较。
相比较。
4、kmp算法的实现
在已知next函数的前提下,根据上面的步骤,kmp算法的实现如下:
int kmp(const std::string& s, const std::string& p, const int sIndex = 0)
{
std::vector<int>next(p.size());
getNext(p, next);//获取next数组,保存到vector中
int i = sIndex, j = 0;
while(i != s.length() && j != p.length())
{
if (j == -1 || s[i] == p[j])
{
++i;
++j;
}
else
{
j = next[j];
}
}
return j == p.length() ? i - j: -1;
}
ok,下面的问题是怎么求模式串 P 的next数组。
next数组的初始条件是next[0] = -1,设next[j] = k,则有:
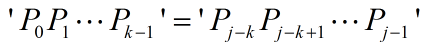
那么,next[j+1]有两种情况:
①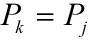 ,则有:
,则有: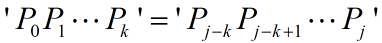
此时next[j+1] = next[j] + 1 = k + 1
②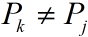 , 如图所示:
, 如图所示:
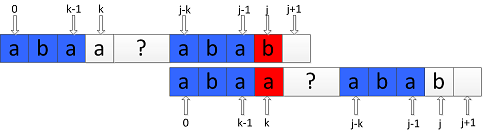
此时需要将P向右滑动之后继续比较P中index为 j 的字符与index为 next[k] 的字符:
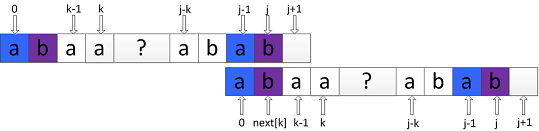
值得注意的是,上面的“向右滑动”本身就是一个kmp在失配情况下的滑动过程,将这个过程看 P 的自我匹配,则有:

如果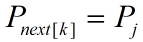 ,则next[j+1] = next[k] + 1;
,则next[j+1] = next[k] + 1;
否则,继续将 P 向右滑动,直至匹配成功,或者不存在这样的匹配,此时next[j+1] = 0。
getNext函数的实现如下:
void getNext(const std::string &p, std::vector<int> &next)
{
next.resize(p.size());
next[0] = -1;
int i = 0, j = -1;
while (i != p.size() - 1)
{
//这里注意,i==0的时候实际上求的是next[1]的值,以此类推
if (j == -1 || p[i] == p[j])
{
++i;
++j;
next[i] = j;
}
else
{
j = next[j];
}
}
}
至此,一个完整的kmp已经实现。
5、getNext函数的进一步优化
注意到,上面的getNext函数还存在可以优化的地方,比如:
i=3
S: a a a b a a a a b
P: a a a a b
j=3
此时,i=3、j=3时发生失配,next[3]=2,此时还需要进行 3 次比较:
i=3, j=2;
i=3, j=1;
i=3, j=0。
而实际上,因为i=3, j=3时就已经知道a!=b,而之后的三次依旧是拿 a 和 b 比较,因此这三次比较都是多余的。
此时应当直接将P向右滑动4个字符,进行 i=4, j=0的比较。
一般而言,在getNext函数中,next[i]=j,也就是说当p[i]与S中某个字符匹配失败的时候,用p[j]继续与S中的这个字符比较。
如果p[i]==p[j],那么这次比较是多余的(如同上面的例子),此时应该直接使next[i]=next[j]。
完整的实现代码如下:
void getNextUpdate(const std::string& p, std::vector<int>& next)
{
next.resize(p.size());
next[0] = -1;
int i = 0, j = -1;
while (i != p.size() - 1)
{
//这里注意,i==0的时候实际上求的是nextVector[1]的值,以此类推
if (j == -1 || p[i] == p[j])
{
++i;
++j;
//update
//next[i] = j;
//注意这里是++i和++j之后的p[i]、p[j]
next[i] = p[i] != p[j] ? j : next[j];
}
else
{
j = next[j];
}
}
}
对应的,只需要在kmp算法中将 getNext(p, next); 替换成 getNextUpdate(p, next); 即可。
6、时间复杂度分析
下面以getNext函数为例,分析kmp算法的时间复杂度。
1 void getNext(const std::string& p, std::vector<int>& next)
2 {
3 next.resize(p.size());
4 next[0] = -1;
5
6 int i = 0, j = -1;
7
8 while (i != p.size() - 1)
9 {
10 if (j == -1 || p[i] == p[j])
11 {
12 ++i;
13 ++j;
14 next[i] = j;
15 }
16 else
17 {
18 j = next[j];
19 }
20 }
21 }
假定p.size()为m,分析其时间复杂度的困惑在于,在while里面不是每次循环都执行 ++i 操作,所以整个while的执行次数不一定为m。
换个角度,注意到在每次循环中,无论 if 还是 else 都会修改 j 的值且每次循环仅对 j 进行一次修改,所以在整个while中 j 被修改的次数即为getNext函数的时间复杂度。
每次成功匹配时,++i; ++j; , 由于 ++i 最多执行 m-1 次,故++j也最多执行 m-1 次,即 j 最多增加m-1次;
对应的,只有在 j=next[j]; 处 j 的值一定会变小,由于 j 最多增加m-1次,故 j 最多减小m-1次。
综上所述,getNext函数的时间复杂度为O(m),若带匹配串S的长度为n,则kmp函数的时间负责度为O(m+n)。
7、kmp的应用优势
①快,O(m+n)的线性最坏时间复杂度;
②无需回朔访问待匹配字符串S,所以对处理从外设输入的庞大文件很有效,可以边读入边匹配。
