原来一直没太搞懂,今天大力搞了搞,感觉比较可了
latex取反是sim
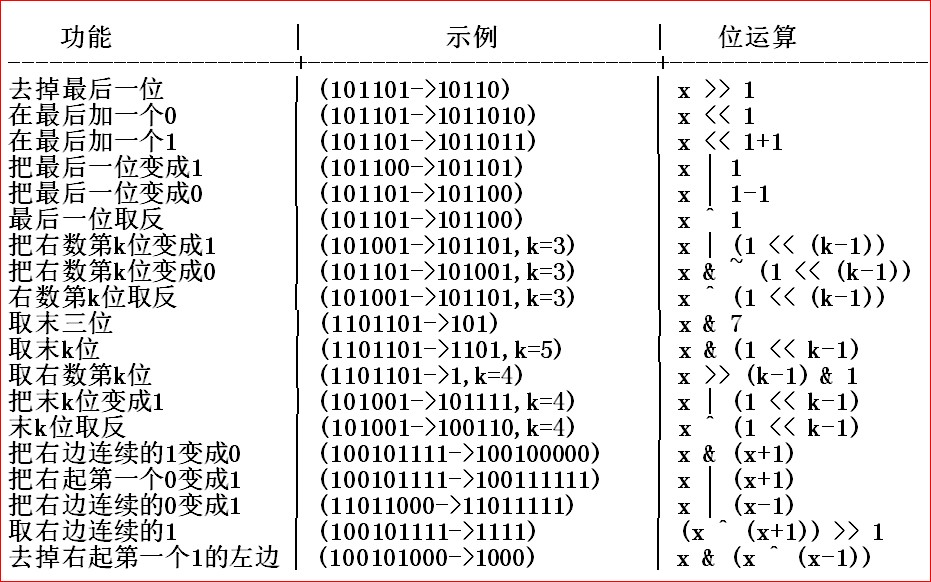
[把数拆成二进制数
所以我们最多只需要2^{n+1}-1的十进制数就好(二进制形式是n个1)\
1.判断一个数字x二进制下第i位是不是1(假设最低为第1位)\
if(1 << (i-1)&x) 操作\
2.将一个数字x二进制第i位改成1\
x = x | (1<<(i-1))\
3.将一个数字x二进制下第i为改成0\
x=x&(sim(1<<(i-1)))取反符号是sim\
4.将一个数二进制下最靠右的一去掉\
x = x&(x-1)
]
状压里提到状态的一维肯定是1<<某某
p1896
[互不侵犯在 n×n(1le nle10) 的棋盘上放 k(0le k<n^2)个国王,国王可攻击相邻的8个格子,求使它们无法互相攻击的方案总数。\
考虑到每行每列之间都有互相的约束关系。因此,我们可以用行和列作为另一个状态的部分。\
我们的三个状态就有了:第几行(用i表示),此行放什么状态(用j表示),包括这一行已经使用了的国王数用s表示\
f[i][j][s]=sum f[i-1][k][s-num[j]]\
首先的问题就是,上文中的k和j怎么表示?\
假设现在第i行的放置状态是这样的:0 0 1 0 1 0 0 1(1代表有国王,0代表没有)\
转换成十进制就是: 41(10) dp:f[i][41][s]\
不过对于每一行的可用状态,我们可以预处理一下,预处理每一行可用可以避免麻烦,还可以优化时间复杂度。\
预处理代码:
]
inline void init(){
cnt=0;
for(int i=0;i<(1<<n);++i)
{
if(i&(i<<1))continue;
int sum=0;
for(int j=0;j<n;++j)
if(i&(1<<j))++sum;
s[++cnt]=i;
num[cnt]=sum;
}return;}
[s数组时用来记录可用状态的十进制\
num数组用来记录该状态的国王数上面例子 国王数为3\
i是枚举所有状态数。假设n=3,那么i枚举的就是:\
000,001,010,011,100,101,110,111\
分别对应十进制0,1,2,3,4,5,6,7\
所以是 i<(1<<n) (i不能到2^3(8))\
if(i&(i<<1))continue;判断相邻国王\
]
//AC代码
#include<bits/stdc++.h>
using namespace std;
int n,m,cnt,MAX;
long long dp[10][200][100];
int can[1000],num[2000];
int getsum(int x)
{
int ret=0;
while (x) ret+=(x&1),x>>=1;
return num[cnt]=ret;
}//预处理函数
int main()
{
register int i,j,k,l,x,y;
long long ans=0;
scanf("%d %d",&n,&m);
MAX=(1<<n)-1;
for (i=0;i<=MAX;i++)
if (!(i&(i<<1))) can[++cnt]=i,dp[1][cnt][getsum(i)]=1;//预处理
for (i=2;i<=n;i++)
{
for (j=1;j<=cnt;j++)
{
x=can[j];
for (k=1;k<=cnt;k++)
{
y=can[k];
if ((x&y)||(x&(y<<1))||(x&(y>>1))) continue;
for (l=0;l<=m;l++) dp[i][j][num[j]+l]+=dp[i-1][k][l];
}
}
}
for (i=1;i<=cnt;i++) ans+=dp[n][i][m];
printf("%lld",ans);
}
p3694 邦邦的大合唱站队
[我们可以设状态i为当前已经排列好的乐队编号集合\
sum[i][j]表示前i个人有几个属于乐队j\
枚举l,r,则有f[i|(1<<j)]=min(f[i|(1<<j)],f[i]+(r-l-(sum[r][j]-sum[l][j])))
]
同理eee
PS.有时间再把P2831康一遍然后把dfs做法写写 咕咕咕