线段树树状数组从入门到跳楼

线性初始化树状数组

void init(){//线性构造
    for (int i = 1; i <= n; i++){
        sum[i] = sum[i - 1] + a[i];
        c[i] = sum[i] - sum[i - lowbit(i)];
    }
}

对于线段树千万不要嫌烦

第一遍可以抄一遍题解，大致了解方法；

第二遍半看半打，加深印象；

第三遍就可以开始自己打；
绝对有效

关于线段树大佬们已经讲的很清楚了，我在这里讲几个蒟蒻容易犯的错误(线段树的坑)：

不开long long见祖宗，要开long long，一定要开

每个修改操作的函数中一定要明确出口（return不能少，具体见代码）

记录线段树数值和懒标记的数组至少要开n的4倍

每打完一部分就要检查，否则你将会献出一上午（大佬请忽略此条）

再码字途中，线段树会出现 int mid=(l+r)/2这样的语句，mid也有的写成m，所以这时要注意分清楚题目中的m(通常是操作次数)和mid

懒标记要下传

懒标记一定要乘区间长度，并注意 大减小 (r-l)，反正这是我犯的一个ZZ错误

不要忘记调用build()函数（不开玩笑，新手经常忘）

当要进行区间乘一个数操作时，懒标记初始要设为1，(而不是加法懒标记初始为0)

当进行多种运算操作是，要注意修改顺序，一般是先乘除，再加减

码字时可以尽量写的散一些，反正就是要自己看着不会头皮发麻，这样检查时很省事

以上的线段树坑来自 luogu 老部长卢晨昕

首先先让我们认识离散化用的函数,STL给我们提供了便利:

unique(start,end);//取出有序序列重复元素,左闭右开,返回去重复序列最后一个元素位置
lower_bound(start,end,key);//左闭右开中寻找第一个大等于key的数,返回值

std::sort(a+1,a+n+1);
cnt = std::unique(a+1,a+n+1) - (a+1)//去重并获得去重后长度cnt,注意减的是初始地址qwq我错了一次
for(int i=1;i<=n;i++)
a[i] = lower_bound(a+1,a+1+cnt,a[i]) - a

感觉原来离散化写的很乱，今天重新修一下

[int~m=unique(a+1,a+n+1)-(a+1);\ 把数组去重,元素放在下标1-n,并获取长度\ int~i = lower\_bound(a+1,a+n+1,x)-a;\ ]

在有序int数组中查找大于等于x的最小整数下标

我们需要对原数组进行一次备份（cp 数组），以便后面的复原

p3755 老c的任务

题解:

树状数组

将点按(x)递增；将询问拆成2个，离线，离散化，按(x)递增排序。按x轴排序，y轴维护树状数组。

然后每次找到一个询问，就判断有哪些点可以加到树状数组中，然后查询一下就好了。把区间询问转化为前缀和相减.

注意题目中边上也算是包含，所以应将左下边界-1；同时坐标必须是正的，还需要+2。
P1972HH的项链

#include<cstdio>
#include<algorithm>
#define maxn 1000005
using namespace std;
int n,l,r;
int num[maxn],tree[maxn],booll[maxn],ans[maxn],q;
struct tre{
	int l,r,pos;
}ask[maxn];
inline int lowbit(int x){return x&(-x);}
bool cmp(tre a,tre b){return a.r < b.r;}
inline void add(int fa,int ad){
	while(fa<=n)
    {
        tree[fa]+=ad;
        fa+=lowbit(fa);
    }
}
inline int sum(int n){
	int ans = 0;
	while(n){
		ans += tree[n];
		n -= lowbit(n);
	}
	return ans;
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	scanf("%d",&num[i]);
	scanf("%d",&q);
	for(int i=1;i<=q;i++)
	{
		scanf("%d%d",&ask[i].l,&ask[i].r);
		ask[i].pos = i;
	}
	sort(ask+1,ask+q+1,cmp);
	int next = 1;
	for(int i=1;i<=q;i++){
		for(int j=next;j <= ask[i].r;j++){
		if(booll[num[j]])
		add(booll[num[j]],-1);//注意这里,仔细理解下
		add(j,1);
        booll[num[j]]=j;}
        next=ask[i].r+1;
        //更新下一次查询的位置
        ans[ask[i].pos]=sum(ask[i].r)-sum(ask[i].l-1);
	}
	for(int i=1;i<=q;i++)
      printf("%d
",ans[i]);
}

P4054计数问题

题解:多维树状数组板子

可以发现 , 矩阵中值的值域很小
(wle 100)考虑暴力思路,

构建(100)个二维树状数组,分别存储各数值 ,在矩阵中出现的次数.

单点修改:将a修改成b,先将a对应的树状数组改掉,对应位置出现次数-1，再对b对应的树状数组对应位置+1

区间查询:直接查询对应子矩阵出现次数即可

#include<cstdio>
#define maxn 301
#define lowbit(x) -x&x
#define ll long long 
using namespace std;
inline int read()
{
    char ch=getchar();int i=0,f=1;
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){i=(i<<1)+(i<<3)+ch-'0';ch=getchar();}
    return i*f;
}

int n,m,q;
int map[maxn][maxn],tree[101][maxn][maxn];

inline void add(int val,int x,int y,int z){//修改操作,将此点权值设为val,并使其次数+=z 
	map[x][y] = val;
	for(int i = x;i <= n;i += lowbit(i))
		for(int j = y;j <= m;j += lowbit(j))
			tree[val][i][j] += z;
}
inline ll sum(int type,int x,int y){//查询1,1到x,y的type出现次数 
	int cnt = 0;
	for(int i = x;i;i -= lowbit(i))
		for(int j = y;j;j -= lowbit(j))
			cnt += tree[type][i][j];
		 return cnt;
}
int main(){
	n=read(),m=read();
	for(int i = 1;i <= n;i++)
		for(int j = 1;j <= m;j++) 
			add(read(),i,j,1);
		q=read();
		for(int i=1;i<=q;i++)
		{
			int opt = read();
			if(opt == 1){
				int x= read(),y=read(),tem=read();
				add(map[x][y],x,y,-1);//原值出现次数-1 
	  			add(tem,x,y,1);//新值出现次数+1 
			}
			else{
				int x1=read(),x2=read(),y1=read(),y2=read(),type=read();
				ll ans1 = sum(type,x2,y2),ans2=sum(type,x1-1,y1-1);
				ll ans = ans2 + ans1 - sum(type,x1-1,y2) - sum(type,x2,y1-1);//容斥
				//sum是不含边界的
				printf("%lld
",ans);
			}
		}
}

线段树:满足区间可加性(f(x,y)=f(f(x,z),f(z,y)),zin[x,y])

线段树以常数大,空间大,难写难调而臭名远扬,但有时也很给力,当然能不写线段树就不写啦,而且记得要开四倍空间

以下部分参考LightHouseOfficial的内容

区间和,区间最大最小值,区间LCA，区间质数个数......可以用线段树维护

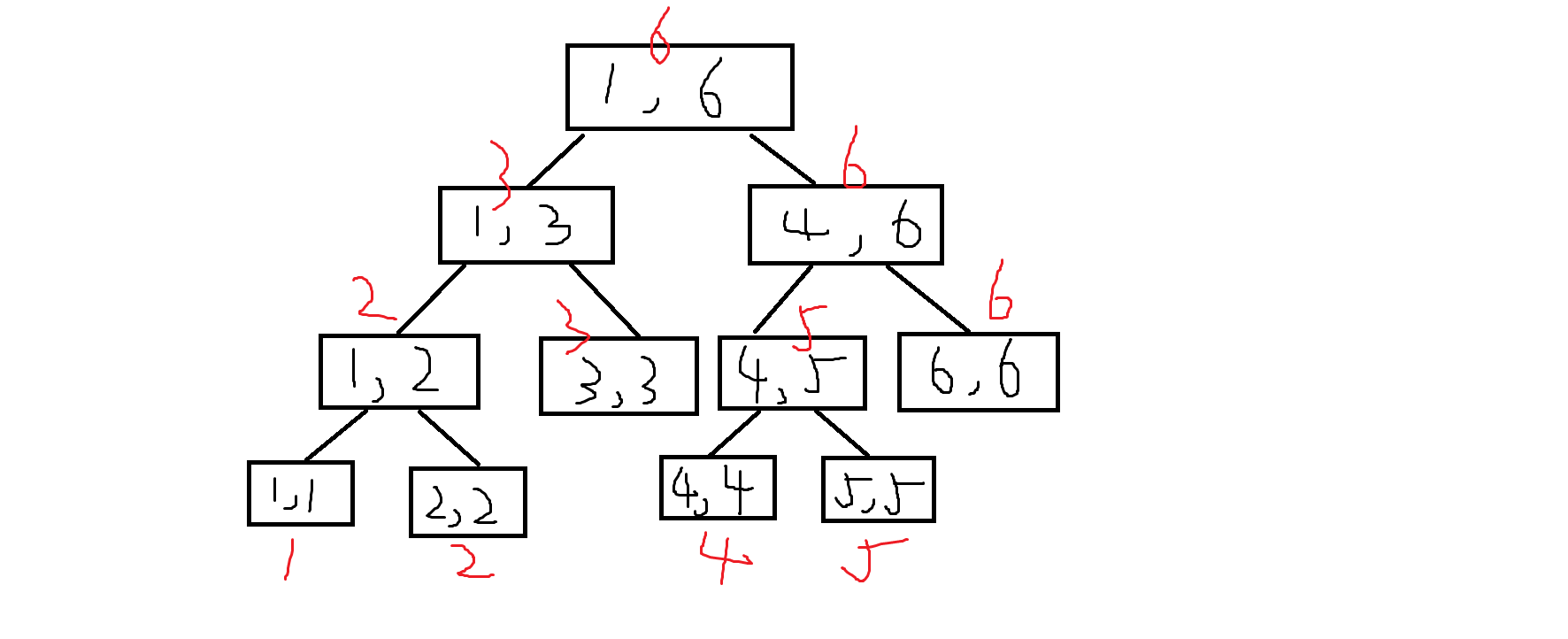
假设数组是{1,2,3,4,5,6}查询区间[2,4]，计算出[2,4]的mid值,mid=(l+r)<<1=3

然后我们查询[l,mid]和[mid+1,r]区间[2,3]和[4,4]

[4,4]是叶子,返回它的值4,回到[2,3]继续递归

p<<1是左儿子,p<<1|1为右儿子

建树:

#define l(x) tree[x].l
#define r(x) tree[x].r
#define val(x) tree[x].val
void pushup(int p){
    val(p)=val(p<<1)+val(p<<1|1);
}
void build(int p,int l,int r){
    l(p)=l,r(p)=r;//保存每个节点的左右儿子的编号
    if(l==r){
        val(p)=a[l];
        return;
    }pushdown(p);
    int mid=(l+r)>>1;
    build(p<<1,l,mid);build(p<<1|1,mid+1,r);//递归建树 
    pushup(p);//更新值
}

int query(int p,int l,int r){//查询区间和 p是fa
    if(l<=tree[p].l && r>=tree[p].r)return tree[p].val;
    pushdown(p);
    int mid=(tree[p].l+tree[p].r)>>1;
    int ret=0;
    if(l<=mid) ret+=query(p<<1,l,r);
    if(r>mid) ret+=query(p<<1|1,l,r);
    return ret;
}

区间修改,打lazytag 然后pushdown

#define val(x) tree[x].val
#define add(x) tree[x].add
void pushdown(int p){
    if(add(p)){
        val(p<<1)+=add(p)*(r(p<<1)-l(p<<1)+1);
        val(p<<1|1)+=add(p)*(r(p<<1|1)-l(p<<1|1)+1);
        add(p<<1)+=add(p);
        add(p<<1|1)+=add(p);
        add(p)=0;
    }
}//加法
void update(int p,int l,int r,int d){//修改
    if(l<=l(p) && r>=r(p)){
        val(p)+=d*(r(p)-l(p)+1);add(p)+=d;
        return;
    }
    pushdown(p);
    int mid=(l(p)+r(p))>>1;
    if(l<=mid)update(p<<1,l,r,d);
    if(r>mid)update(p<<1|1,l,r,d);
    pushup(p);
}

动态开点线段树

由于线段树要maxn<<2,maxn过大显然MLE,这时就要离散化或动态开点了

意思是，你要用到一个点才开那个点，不用的点不开，可以大幅节省空间，空间复杂度降为O(nlogn)

(log_210^6approx20)是不是很给力

接下来是实现：

一开始，你只有一个根节点。

通过update函数往树里面插点，开两个数组记录每个节点的左右儿子编号。

递归进入左右儿子，如果要用新点，就开新点。

可持久化线段树

对于每个询问我们每次不开一整棵树，而是每次把修改节点插入，也就是插入一些历史节点来储存历史值。

空间复杂度成了(nlog^2n)，一般开32倍空间<<5

一般可持久化线段树的题目只要求单点修改，区间修改可以实现不过复杂度比较高。

真的遇到了需要写主席树而且要求区间修改的题目，一般可以转化为单点修改进行操作

时间复杂度((n+m)logn)
还没完咕咕咕