斜率 优化 dp

(large斜率优化dp)

//P2365
#include<cstdio>
#define ll long long
using namespace std;
ll f[5010],sumt[5010],sumc[5010];
int n,s;
ll min(int a,int b){return a<b?a:b;}
signed main(){
 int n,s,t,c;
    scanf("%d%d",&n,&s);
    for (int i=1;i<=n;++i){
        scanf("%d%d",&t,&c);
        sumt[i]=sumt[i-1]+t;
        sumc[i]=sumc[i-1]+c;
    }
    for (int i=1;i<=n;++i)
        f[i]=0x3f3f3f3f;
    for (int i=1;i<=n;++i)
    for (int j=0;j<=i-1;++j)
        f[i]=min(f[i],f[j]+sumc[i]*sumt[i]+s*sumc[n]-sumc[j]*(sumt[i]+s));
    printf("%d",f[n]);
    return 0;
}

[luoguP2365\ F[i]=min_{0le j<i}{F[j]+sumT[i]*(sumC[i]-sumC[j]+S*(sumC[N]-sumC[j])) }O(n^2)\ luoguP5785\ 数据超级加倍\ 对上式子进行优化,把常数,仅与i有关的项,仅与j有关的项以及i,j乘积项分离\ F[i]=min_{0le j<i}{ F[j]-(S+sumT[i])*sumC[j]}+sumT[i]*sumC[i]+S*sumC[N];\ 去掉min,把关于j的看做变量F[j]和sumC[j],其余部分看做常量\ 得到F[j]=(S+sumT[i])*sumC[j]+F[i]-sumT[i]*sumC[i]-S*sumC[N];\ 以sumC[j]为横坐标,F[j]为纵坐标,建立坐标轴,进行线性规划\ 斜率: sumT(i)+S\ 纵截距: f(i)−sumT(i)×sumC(i)−S×sumC(n)\ 我们可以发现纵截距越大,F[i]越大\ 通俗一点讲，所谓选择最优决策点就是把一条直线从下向上靠，第一个相交的点就是最优决策点（因为此时b最小，f_i也必定最小）。 ]

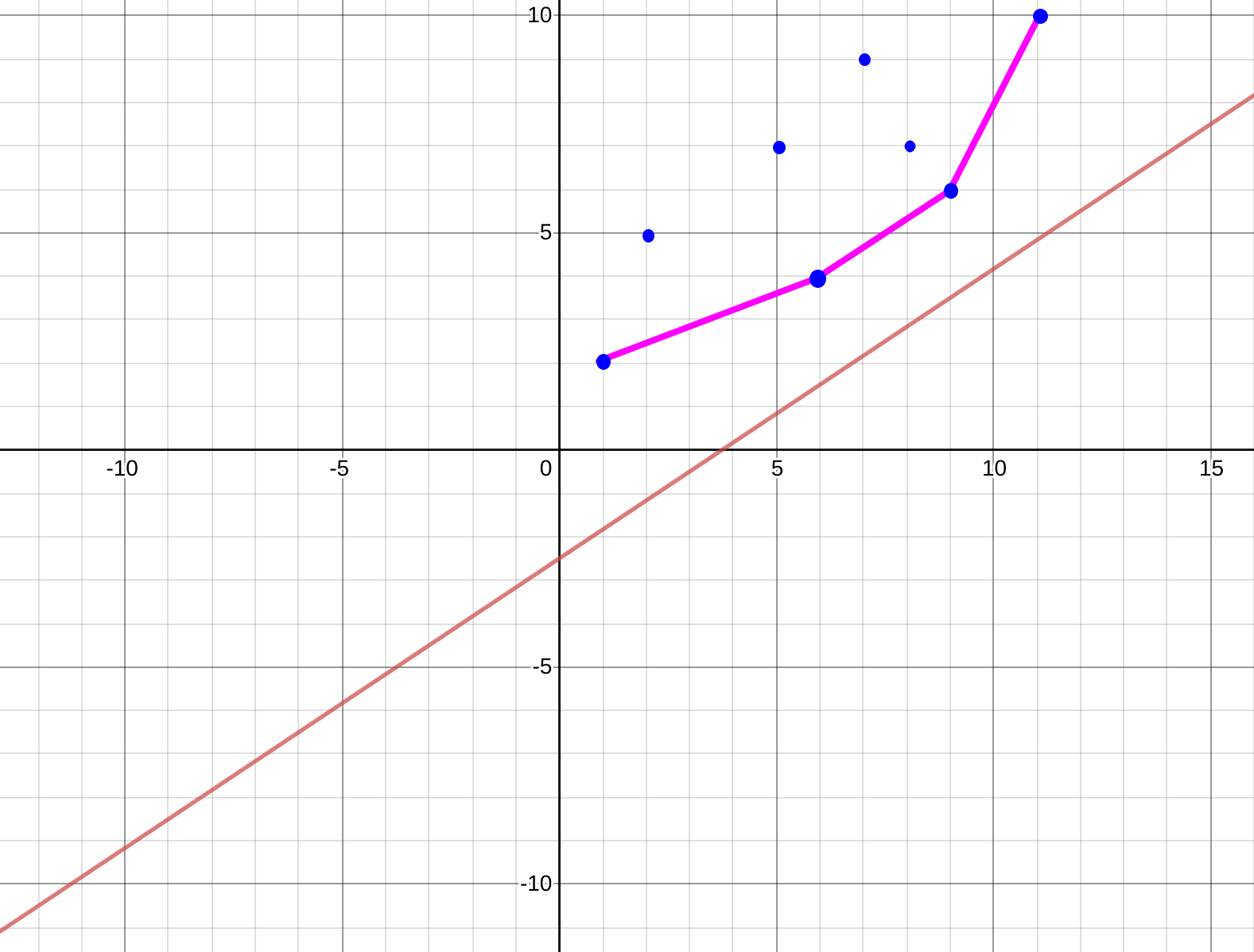
偷的Chpu437的图 23333

取所有的点,寻找一个凸包(凸多边形)使其围住所有点在凸包上进行线性规划

为了探究最佳决策需要满足的条件, 我们设三个决策为(j_1,j_2,j_3,且j_1<j_2<j_3)

从图可以发现,(j_2)有可能成为最优结构,当且仅当:

[frac{F[j_2]-F[j_1]}{sumC[j_2]-sumC[j_1]}<frac{F[j_3]-F[j_2]}{sumC[j_3]-sumC[j_2]} ]

在下凸壳,斜率单调递增,下凸壳的顶点才可能成为最优决策,对于某条斜率为k的直线,某顶点左侧线段斜率比k小,

右侧线段比k大,顶点为最优决策,直线斜率满足单调

同时, 由于 sumC 单调递增, 新决策的横坐标一定大于旧决策, 又因为 sumT 单调递增, S+sumT(i), 即 kl 单调递增, 如果我们对于凸壳上每两个相邻顶点的截距, 只保留大于 kl 的部分, 那么最优决策一定在这个凸壳的左端点上.

所以我们建立一个单调队列,若斜率((F[q[l+1]]-F[q[l]])/(sumC[q[l+1]]-sumC[q[l]])le S+sumT[i])，则把(q[l])出队

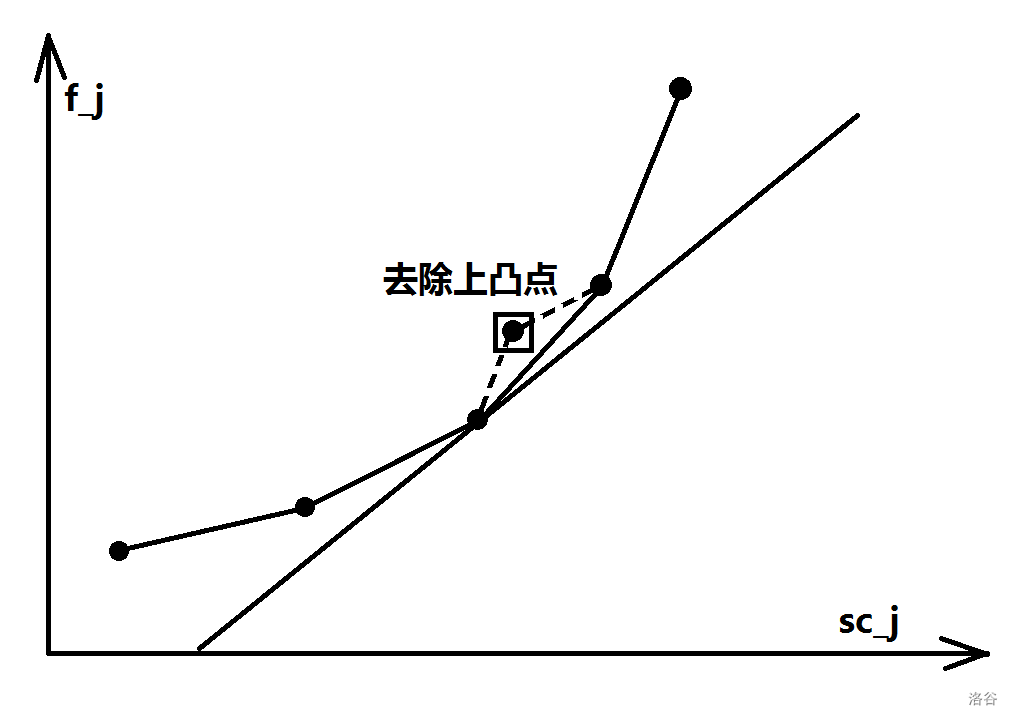
luogu Stay_Hungry 大佬的图

复杂度为O(n)

代码先咕会 咕咕咕

对于斜率为负数时,要找下凸点,维护下凸包