C#数据结构_查找

查找：静态查找和动态查找。

衡量查找算法的最主要的标准是平均查找长度（Average Search Length，简 称 ASL）。平均查找长度是指在查找过程中进行的关键码比较次数的平均值。

顺序查找(Sequnce Search)又称线性查找(Linear Search)，其基本思想是：从 静态查找表的一端开始，将给定记录的关键码与表中各记录的关键码逐一比较， 若表中存在要查找的记录，则查找成功，并给出该记录在表中的位置；否则，查找失败，给出失败信息。

    public int SeqSearch(SeqList<int> sqList, int data)
    {
        sqList[0] = data;
        int i = 0;
        for (i = sqList.GetLength(); sqList[i] > data; --i);
        {
            return i;
        }
    }

折半查找(Binary Search)又叫二分查找，其基本思想是：在有序表中，取中 间的记录作为比较对象，如果要查找记录的关键码等于中间记录的关键码，则查 找成功；若要查找记录的关键码小于中间记录的关键码，则在中间记录的左半区 继续查找；若要查找记录的关键码大于中间记录的关键码，则在中间记录的右半 区继续查找。不断重复上述查找过程，直到查找成功，或有序表中没有所要查找 的记录，查找失败。

    public int BinarySearch(SeqList<int> sqList, int key)
    {
        sqList[0] = key;    //0单元存放要查找的记录
        int mid = 0;
        int flag = -1;
        int low = 1;    //设置初始区间的下限值
        int high = sqList.GetLength();    //设置初始区间的上限值
        //记录没有查找完
        while (low <= high)
        {
            //取中点
            mid = (low + high)/2;
            //查找成功，记录位置存放到flag中
            if (sqList[0] == sqList[mid])
            {
                flag = mid;
                break;
            }
            //调整到左半区
            else if(sqList[0] < sqList[mid])
            {
                high = mid -1;
            }
            //调整到右半区
            else
            {
                low = mid    + 1;
            }
        }
        if (flag > 0)
        {
            Console.WriteLine("Search is successful!");
            return flag;
        }
        else
        {
            Console.WriteLine("Search is failing!");
            return -1;
        }
    }

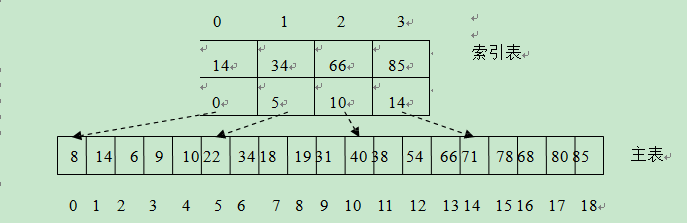
索引查找(Index Search)又称分块查找。比如，对于下图现在要查找关键码为 54 的记录。先将 54 依次与索 引表中每个记录的 data 域的值进行比较，由于 34<54<66，则若在主表中存在关 键码为 54 的记录，则该记录必定在主表的第 3 个子表中。由于相应的 link 域的 值为 10，所以，从主表的第 11 个记录（数组的下标为 10）开始进行顺序查找。 当比较到主表的第 13 个记录（数组的下标为 12）时，关键码相等，说明主表中 有要查找的记录，则查找成功。当然，如果比较到第 15 个记录（因为索引表的 下一个记录的 link 域的值为 14）仍然不等，说明主表中不存在要查找的记录， 查找失败。

二叉排序树查找过程为：

（1）若二叉排序树为空，则查找失败（下面的算法实现以返回 1 表示查找 失败）；

（2）若二叉排序树非空，则将给定记录的关键码与二叉排序树根结点的关 键码进行比较，如果相等，则查找成功（下面的算法实现以返回 0 代表查找成功）， 查找过程结束。否则，执行以下两步中的一步；

（3）若给定记录的关键码小于二叉排序树根结点的关键码，查找将在根结 点的左子树上继续进行，转（1）；

（4）若给定记录的关键码大于二叉排序树根结点的关键码，查找将在根结 点的右子树上继续进行，转（1）。

二叉排序树上的查找算法的实现如下：

    public int Search(BiTree<int> bt, int key)
    {
        Node<int> p;

        //二叉排序树为空
        if (bt.IsEmpty() == true)
        {
            Console.WriteLine("The Binary Sorting Tree is empty!");
            return 1;
        }
        p = bt.Head;
        //二叉排序树非空
        while (p != null)
        {
            //存在要查找的记录
            if (p.Data == key)
            {
                Console.WriteLine("Search is Successful!");
                return 0;
            }
            //待查找记录的关键码大于结点的关键码
            else if (p.Data < key)
            {
                p = p.LChild;
            }
            //待查找记录的关键码小于结点的关键码
            else
            {
                p = p.RChild;
            }
        }
        return 1;
    }

哈希法主要考虑两个问题，其一是如何构造哈希函数，其二是如何解 决哈希冲突

常用的哈希函数构造方法：直接定址法；除留余数法；数字分析法；平方取中法；

解决哈希冲突：

开放地址法：是指当由关键码得到的哈希地址一旦产生冲突，即该地址中已经存放了记录，就去寻找下一个哈希地址，直到找到空的哈希地址为止。

二次探测法：线性探测法由于是一个地址单元一个地址单元探测，探测的增量是线性的，所以容易产生堆积问题。

 链表法：用链表法解决哈希冲突有两种方法：

第一种方法是把所有的同义词用单链表链接起来；

第二种方法是当哈希表中相应位置为空时直接存放，当哈希表中相应 位置非空时用单链表链接起来。