原创作品,转载请注明出处哦~
RNN: Feed Forward, Back Propagation Through Time and Truncated Backpropagation Through Time
了解RNN的前向、后向传播算法的推导原理是非常重要的,这样,
1. 才会选择正确的激活函数;
2. 才会选择合适的前向传播的timesteps数和后向传播的timesteps数;
3. 才会真正理解为什么会梯度消失和爆炸;
4. 才会从根源上想怎样尽量去避免梯度消失和梯度爆炸;
5. 才会知道为什么Attention的提出的意义;
6. 才会知道Google Transformer这个模型设计时候,是怎么想到要这样做的……
原来这些都是联系在一起的,都是由于传播的原理所决定的。
现在把看到的资料和自己的想法总结一下,分享给大家,欢迎批评指正。
参考资料:Ilya Sutskever, Training Recurrent Neural Networks, Thesis, 2013
1. RNN的前向传播
<1> 前向传播过程与损失函数
给定一个输入序列$(v_1, ..., v_T)$ (我们用$v_1^T$表示), RNN通过以下算法计算隐层状态 $h_1^T$ 和 序列的输出 $z_1^T$:
1: for $t$ from $1$ to $T$ do
2: $u_t leftarrow W_{hv}v_t + W_{hh}h_{t - 1} + b_h$
3: $h_t leftarrow e(u_t)$
4: $o_t leftarrow W_{oh}h_t + b_o$
5: $z_t leftarrow g(o_t)$
6: end for
其中,$e(cdot)$ 和 $g(cdot)$ 分别是隐层和输出层的非线性激活函数。$h_0$是存储第一个隐层状态的向量表示。那么RNN的损失函数可以表示为各个时间步(timestep)的损失之和:
$$L(z , y) = sum_{t = 1}^TL(z_t; y_t) ag1$$
<2> 激活函数的选择
这部分内容是参考《百面机器学习》这本书的介绍。公式推导还是采用<1>中的符号表示。
Question: 在循环神经网络中能否使用ReLU作为损失函数?
Answer: 可以的。但是需要对矩阵的初始值做一定的限制,否则十分容易引发数值问题。原因如下:
(1) 首先是前向传播中的第 $T$ 个单元的数值可能趋于0或无穷的问题
对于RNN的前向传播过程,有
$$u_t leftarrow W_{hv}v_t + W_{hh}h_{t - 1} + b_h ag2$$
$$h_t leftarrow e(u_t) ag3$$
那么将 $h_{t-1}$ 的(1)形式的表示带入(2)中,得到:
$$u_t leftarrow W_{hv}\,v_t + W_{hh}\,e(W_{hv}v_{t-1} + W_{hh}\,h_{t - 2} + b_h ) + b_h ag4$$
若采用ReLU代替公式中的激活函数 $e(cdot)$ ,并且假设ReLU函数一直处于激活状态(e(x) = x), 则有
$$u_t leftarrow W_{hv}\,v_t + W_{hh}(W_{hv}v_{t-1} + W_{hh}\,h_{t - 2} + b_h ) + b_h ag5$$
继续将其展开,会得到 $T$ 个 $W$连乘。如果 $W$ 不是单位矩阵,最终结果将会趋于0或无穷,引发严重的数值问题。
(2) 在反向传播中同样非常容易出现梯度消失或爆炸的问题
$$frac{ partial{u_t}}{partial{u_{t-1}}} = W_{hh}cdot diag[e'(u_{t - 1})] ag6$$
(推导过程这里先不介绍,<2>中会有更详细的推导)
若采用ReLU代替公式中的激活函数 $e(cdot)$ ,并且假设ReLU函数一直处于激活状态(e(x) = x), 则 $diag[e'(u_{t - 1})]$为单位矩阵,有$frac{ partial{u_t}}{partial{u_{t-1}}} = W_{hh}$。在经历了$t$层梯度传递后,$frac{ partial{u_t}}{partial{u_{1}}} = (W_{hh})^t$。那么,即使采用了ReLU函数,只要 $W$ 不是单位矩阵,梯度还是会出现消失或者爆炸的情况。
(3) 为什么CNN中不会出现这样的问题?
Answer: 因为CNN中每一层的卷积权重不同,并且初始化时它们是独立同分布的,因此可以相互抵消,多层之后一般不会出现严重的数值问题。而RNN中则是公用的权值矩阵W,因此~
(4) 如果用ReLU怎样尽量避免这样的数值问题呢?
当采用ReLU作为循环神经网络中隐层的激活函数时,只有当$W$的取值在单位矩阵附近时才能有较好效果,因此需要将 $W$ 初始化为单位矩阵。实验证明,初始化$W$为单位矩阵并使用ReLU为激活函数,在一些应用中与LSTM模型效果相当,并且学习速度比LSTM更快,是一个值得尝试的小技巧。
2. RNN: Back Propagation Through Time
找了一些资料,Ilya Sutskever, Training Recurrent Neural Networks, Thesis, 2013中给出的算法如下所示,但是个人以为,其在计算$W_hh$时有问题。
1: for $t$ from $T$ to $1$ do
2: $mathrm{d}{o_t} leftarrow {g'(o_t)} cdot {frac{mathrm{d}{L(z_t;\, y_t)}}{mathrm{d}{z_t}}}$
3: $mathrm{d}b_o leftarrow mathrm{d}b_o + mathrm{d}o_t$
4: $mathrm{d}W_{oh} leftarrow mathrm{d}W_{oh} + mathrm{d}o_t h_t^{mathrm{T}}$
5: $mathrm{d}h_t leftarrow mathrm{d}h_t + W_{oh}^{mathrm{T}} mathrm{d}o_t$
6: $mathrm{d}u_t leftarrow {e'(u_t)} cdot mathrm{d}h_t$
7: $mathrm{d}W_{hv} leftarrow mathrm{d}W_{hv} + mathrm{d}u_tv_t^mathrm{T}$
8: $mathrm{d}b_h leftarrow mathrm{d}b_h + mathrm{d}u_t$
9: $mathrm{d}W_{hh} leftarrow mathrm{d}W_{hh} + mathrm{d}u_th_{t - 1}^mathrm{T}$
10: $mathrm{d}h_{t - 1} leftarrow W_{hh}^mathrm{T}mathrm{d}u_t$
11: end for
12: Return $mathrm{d} heta = [mathrm{d}W_{hv}, mathrm{d}W_{hh}, mathrm{d}W_{oh}, mathrm{d}b_h, mathrm{d}b_o, mathrm{d}h_{color{Red}0}]$
其中,表红色的是数字'0'而不是字母'o'。
这里3,4,5,7,8,9行的变量梯度是沿时间累加的。
在传播过程中,并没有更新变量值,而是每一时刻都存储着当前时刻的梯度,从T时刻到1时刻,反向传播完成后,return来对变量值进行更新。
-----------正确求解$frac{partial L}{partial W_{hh}}$的方法如下:--------------
在计算梯度时,有一点要非常注意:
$$u_t leftarrow W_{hv}v_t + W_{hh}h_{t - 1} + b_h ag2$$
中,对$W_{hh}$求偏导时,要注意(2)式中,既要对$W_{hh}$求偏导,$h_{t - 1}$也是关于$W_{hh}$的函数,所以$h_{t - 1}$也要对$W_{hh}$求偏导!
也就是说,当计算$frac{partial L_t}{partial W_{hh}}$时,取决于$h_{t - 1}$,$h_{t - 2}$, ... ,$h_1$。
举个简单的例子,把无关变量W_{hv}所在一项看做常数a,偏置设为0:
$$S_k = a + WS_{k-1} ag7$$
$$frac{partial{S_k}}{partial{W}} = frac{partial{S_k}}{partial{W}} + frac{partial{S_k}}{partial{S_{k-1}}} cdot frac{partial{S_{k-1}}}{partial{W}} ag8$$
这样写不严谨,但方便说明: $frac{partial{S_k}}{partial{W}}$是将(7)中的 $S_{k -1}$ 看做常数,对 $W$ 求偏导得到;$frac{partial{S_k}}{partial{S_{k-1}}} cdot frac{partial{S_{k-1}}}{partial{W}}$ 是将(7) 中的$S_{k-1}$对$W$求偏导得到。那么,
$$frac{partial{S_k}}{partial{W}} = frac{partial{S_k}}{partial{W}} + frac{partial{S_k}}{partial{S_{k-1}}} cdot frac{partial{S_{k-1}}}{partial{W}}$$
$$ = frac{partial{S_k}}{partial{W}} + frac{partial{S_k}}{partial{S_{k-1}}} cdot [ frac{partial{S_{k-1}}}{partial{W}} + frac{partial{S_{k-1}}}{partial{S_{k-2}}} cdot frac{partial{S_{k-2}}}{partial{W}}]$$
$$ = frac{partial{S_k}}{partial{W}} + frac{partial{S_k}}{partial{S_{k-1}}} cdot frac{partial{S_{k-1}}}{partial{W}} + frac{partial{S_k}}{partial{S_{k-1}}} cdot frac{partial{S_{k-1}}}{partial{S_{k-2}}} cdot frac{partial{S_{k-2}}}{partial{W}} + frac{partial{S_k}}{partial{S_{k-1}}} cdot frac{partial{S_{k-1}}}{partial{S_{k-2}}} cdot cdot cdot frac{partial{S_1}}{partial{W}} ag9$$
举个例子:
$$frac{partial L_3}{partial W_{hh}} =frac{partial L_3}{partial h_3} cdot frac{partial h_3}{partial u_3}cdot frac{partial u_3}{partial W_{hh}}$$
$$+ frac{partial L_3}{partial h_3} cdot frac{partial h_3}{partial u_3}cdot frac{partial u_3}{partial h_2} cdot frac{partial h_2}{partial u_2} cdot frac{partial u_2}{partial W_{hh}}$$
$$+ frac{partial L_3}{partial h_3} cdot frac{partial h_3}{partial u_3}cdot frac{partial u_3}{partial h_2} cdot frac{partial h_2}{partial u_2} cdot frac{partial u_2}{partial h_1} cdot frac{partial h_1}{partial u_1} cdot frac{partial u_1}{partial W_{hh}} ag{10}$$
$$frac{partial L_2}{partial W_{hh}} =frac{partial L_2}{partial h_2} cdot frac{partial h_2}{partial u_2}cdot frac{partial u_2}{partial W_{hh}}$$
$$+ frac{partial L_2}{partial h_2} cdot frac{partial h_2}{partial u_2}cdot frac{partial u_2}{partial h_1} cdot frac{partial h_1}{partial u_1} cdot frac{partial u_1}{partial W_{hh}} ag{11}$$
$$frac{partial L_1}{partial W_{hh}} =frac{partial L_1}{partial h_1} cdot frac{partial h_1}{partial u_1}cdot frac{partial u_1}{partial W_{hh}} ag{12}$$
那么,反向传播T时间后,对$W_{hh}$ 权值进行更新。
$$frac{partial L}{partial W_{hh}} = frac{partial L_1}{partial W_{hh}} + frac{partial L_2}{partial W_{hh}} + frac{partial L_3}{partial W_{hh}} ag{13}$$
其梯度为(10)(11)(12)所求值之和。
那么,$$W_{hh} leftarrow W_{hh} + gamma Delta W_{hh} ag{14}$$
这样,RNN梯度爆炸和衰减的原因也明了了。RNN的传播机制类似于“蝴蝶效应”,在不断的权值相乘中,一点点小的变动都会在t时间的传播中被指数级放大。那么在输入句子长度较大时,学习长程依赖关系会变得很困难。
为了更好地学得句子长程依赖关系,有一些方法,比如我们熟知的LSTM,GRU等,本文不做赘述。本文要介绍的是Truncated Backpropagation Through Time,通过调节RNN正向、反向传播的时间步长度,在一定程度上缓解RNN传播中的数值问题。
3. RNN: Truncated Back Propagation Through Time
<1> TBPTT 算法简介
TBPTT (Truncated Back Propagation Through Time) 可能是训练RNN中最实用的方法。
BPTT有一个主要的问题:对单个参数的更新的cost很高,这样RNN就很难适应大数量的迭代。举个例子,对长度为1000的输入序列进行反向传播,其代价相当于1000层的神经网络进行前向后向传播。
Naive的改进方法: 如果可以把这个长度为1000的句子切分成50个长度为20的句子,然后将每个长度为20的句子单独训练,那么计算量就会大大降低。
但是,该方法只能学得这每个切分部分内部的依赖关系,而无法看到20个时间步之外的更多时序依赖关系。
TBPTT:类似与Naive的方法,但有一点改进。
TBPTT中,每次处理一个时间步,每前向传播 $k_1$ 步,后向传播 $k_2$ 步。如果 $k_2$ 比较小,那么其计算代价将会降低。这样,它的每一个隐层状态可能经过多次时间步迭代计算产生的,也包含了更多更长的过去信息。在一定程度上,避免了naive方法中无法获取截断时间步之外信息的问题。
TNPTT算法:
1: for $t$ from 1 to $T$ do
2: Run the RNN for one step, computing $h_t$ and $z_t$
3: if $t$ divides $k_1$ then
4: Run BPTT(as described in 2), from $t$ down to $t - k_2$
5: end if
6: end for
那么k1, k2应该选多大呢?
<2> $k_1$, $k_2$ 大小选择
参考链接:https://machinelearningmastery.com/gentle-introduction-backpropagation-time/
首先需要想,$k_1$, $k_2$ 是做什么的呢?
$k_1$: 每经过k1时间步的前向传播,对参数进行一次更新。那么由于k1控制着参数更新的频率,其也影响着训练的速度快慢。
$k_2$: 需要进行BPTT的时间步数。一般来说,它需要大一些,来获取更多的时序信息。但是过大又会引起梯度数值问题。
符号$n$表示序列总时间步的长度。
(1) TBPTT(n, n): 传统的BPTT
(2) TBPTT(1, n): 每向前处理一个时间步,便后向传播所有已看到的时间步。(Williams and Peng提出的经典的TBPTT)
(3) TBPTT($k_1$,1): 网络并没有足够的时序上下文来学习,严重的依赖内部状态和输入。
(4) TBPTT($k_1$,$k_2$), where$k_1$ < $k_2$ < n: 对于每个序列,都进行了多次更新,可以加速训练。
(5) TBPTT(k1,k2), where k1=k2: 同Naive方法。
在TensorFlow中默认采用的是(5)这个方式。
In order to make the learning process tractable, it is common practice to create an "unrolled" version of the network, which contains a fixed number (
num_steps) of LSTM inputs and outputs. The model is then trained on this finite approximation of the RNN. This can be implemented by feeding inputs of lengthnum_stepsat a time and performing a backward pass after each such input block.
TensorFlow 中采用的 TBPTT(k1, k2),其中(k1 = k2 = num_steps) 实现方式的图示:
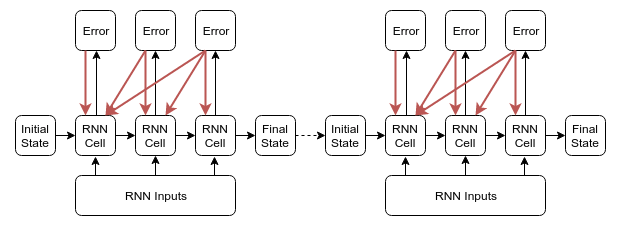
图1. TensorFlow TBPTT方式图示
上图来源于 https://r2rt.com/styles-of-truncated-backpropagation.html
在这篇blog中,通过代码实现对比了这位作者想验证的TBPTT(1, k2) 和 TensorFlow中这种的优劣。
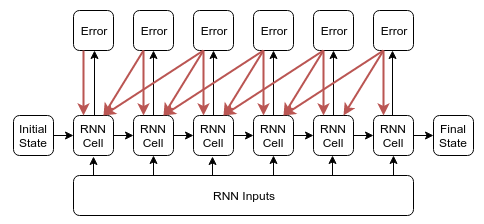
图2. TBPTT(1, k2) 反向传播的图示
具体内容大家可以参考上面网页链接详细阅读。
这位博主实验得出的结论:
1. 对于相同的时间步:TBPTT(1, k2) 优于 TBPTT(k1, k2)
2. 对于相同的序列长:TBPTT(1, k2) 丧失了优势。
同时给出两点建议:
1. TBPTT(1, k2) 和 TBPTT(1, n) (其中n表示序列总长) 的时间代价相差不大,并且TBPTT(1, n)效果会更好一点,因此并不是很有必要采用TBPTT(1, k2);
2. 由实验得知,在相同时间步时,TensorFlow的TBPTT(k1, k2)效果并不如TBPTT(1, k2),这表示TBPTT(1, k2) 可能不能学得更加全面的序列的信息(同上文分析的naive方式的不足),因此,可以考虑采用TBPTT(k1, k2)(其中k1 < k2 < n)这种方式。
============================================================
4. 番外篇
这样RNN的正向和反向传播就整理完毕了。最后说一些自己的小发现,就是对Transformer模型设计的理解。
虽然Attention Is All You Need这篇论文拿在手里看过很久了,The Illustrated Transformer这篇blog对其算法实现做了很详细生动的讲解,The Annotated Transformer这篇用pytorch实现模型,同样给出了非常详尽的介绍。但自己之前只是知道它是如何实现的,知道它效果不错,但是却没想过,这个模型的设计者当初是怎么想到用这个方法来做的。现在想了想,可能并不对,但也算是把这些内容串起来了。
1. 首先看Seq2Seq模型吧,从encoder对输入序列进行编码,所有输入内容最终都被编码进encoder的最后一个单元,自然会面临 前文所述的数值问题的风险,也可能因为维度原因无法表征整个输入序列的完整信息,也可能因为输入序列很长,到最后一个单元不能很好的存储长程依赖关系等等。
2. 之后在decoder中加入了attention机制,每翻译一个token, 都回看encoder中的各个输入$x_t$的隐层表示$h_t$,计算相似度,求得context的表征,作为辅助信息 输入到decoder的单元中,做预测。
这样的确每次翻译一个token时,可以将重点放在encoder输入的与预测词相关的词的$h_t$上,但是,只要用到了RNN,其在前向、后向传播中,还是用的这一套算法理论,还是有$W$权值的累乘,那么,还是会有这样的数值问题的可能。
那么,有没有什么办法,可以不用引入这样的$W$的累乘呢?
我们可不可以直接将decoder的词与encoder的输入求相似度呢?而不是与encoder的前向后向传播之后(引入了$W$的累乘之后)的$h_t$求相似度呢?
这样self-attention就出现了。
3. 可以把self-attention中两两单词之间经过attetion后获得的sum的表征,类比与RNN的前向后向传播后获取的$h_t$,它们都表示该词与整个序列上下文的关系。
那么,transformer中,encoder的self-attention可以类比RNN前向后向传播获取隐层表征$h_t$,以此获取每个输入词与输入序列上下文的关系;
每预测一个词的时候,decoder就用其作为query来查encoder中的key, value,做出预测;
每预测出一个词,就是一次训练,更新参数;之后拿着已经预测出的1~t个词,作为decoder的输入,再预测第t + 1的词。transformer中decoder的self-attention同样相当于Seq2Seq2中decoder获取$h'_t$.
之后,transformer同样需要用decoder的query来查encoder中的key-value,完成最终预测。
思想基本就是,用self-attention获取的加权value的sum表征,代替隐层状态$h_t$,表示每个词与上下文的关系。
但是,self-attention只用到了两两词之间向量相似度的运算,而这些向量中并没有词的相对位置的信息,因此,transformer的最大问题就是,目前还没有完美的获取position的方法。虽然有论文中提出的绝对位置编码,后面google又提出相对位置编码,但只要在做self-attention这个运算中,没有用到位置信息,这个问题就还不能彻底解决。
(番外篇这些话,是自己的想法,可能并不严谨。)
=======================================
 [支付宝] 您的鼓励是我的光~ O(∩_∩)O
[支付宝] 您的鼓励是我的光~ O(∩_∩)O