看了很多博客,关于关联规则的介绍想做一个详细的汇总:
一、概念
表1 某超市的交易数据库
|
交易号TID |
顾客购买的商品 |
交易号TID |
顾客购买的商品 |
|
T1 |
bread, cream, milk, tea |
T6 |
bread, tea |
|
T2 |
bread, cream, milk |
T7 |
beer, milk, tea |
|
T3 |
cake, milk |
T8 |
bread, tea |
|
T4 |
milk, tea |
T9 |
bread, cream, milk, tea |
|
T5 |
bread, cake, milk |
T10 |
bread, milk, tea |
定义一:设I={i1,i2,…,im},是m个不同的项目的集合,每个ik称为一个项目。项目的集合I称为项集。其元素的个数称为项集的长度,长度为k的项集称为k-项集。引例中每个商品就是一个项目,项集为I={bread, beer, cake,cream, milk, tea},I的长度为6。
定义二:每笔交易T是项集I的一个子集。对应每一个交易有一个唯一标识交易号,记作TID。交易全体构成了交易数据库D,|D|等于D中交易的个数。引例中包含10笔交易,因此|D|=10。
定义三:对于项集X,设定count(X⊆T)为交易集D中包含X的交易的数量,则项集X的支持度为:
support(X)=count(X⊆T)/|D|
引例中X={bread, milk}出现在T1,T2,T5,T9和T10中,所以支持度为0.5。
定义四:最小支持度是项集的最小支持阀值,记为SUPmin,代表了用户关心的关联规则的最低重要性。支持度不小于SUPmin 的项集称为频繁集,长度为k的频繁集称为k-频繁集。如果设定SUPmin为0.3,引例中{bread, milk}的支持度是0.5,所以是2-频繁集。
定义五:关联规则是一个蕴含式:
R:X⇒Y
其中X⊂I,Y⊂I,并且X∩Y=⌀。表示项集X在某一交易中出现,则导致Y以某一概率也会出现。用户关心的关联规则,可以用两个标准来衡量:支持度和可信度。
定义六:关联规则R的支持度是交易集同时包含X和Y的交易数与|D|之比。即:
support(X⇒Y)=count(X⋃Y)/|D|
支持度反映了X、Y同时出现的概率。关联规则的支持度等于频繁集的支持度。
定义七:对于关联规则R,可信度是指包含X和Y的交易数与包含X的交易数之比。即:
confidence(X⇒Y)=support(X⇒Y)/support(X)
可信度反映了如果交易中包含X,则交易包含Y的概率。一般来说,只有支持度和可信度较高的关联规则才是用户感兴趣的。
定义八:设定关联规则的最小支持度和最小可信度为SUPmin和CONFmin。规则R的支持度和可信度均不小于SUPmin和CONFmin ,则称为强关联规则。关联规则挖掘的目的就是找出强关联规则,从而指导商家的决策。
这八个定义包含了关联规则相关的几个重要基本概念,关联规则挖掘主要有两个问题:
- 找出交易数据库中所有大于或等于用户指定的最小支持度的频繁项集。
- 利用频繁项集生成所需要的关联规则,根据用户设定的最小可信度筛选出强关联规则。
目前研究人员主要针对第一个问题进行研究,找出频繁集是比较困难的,而有了频繁集再生成强关联规则就相对容易了。
二、理论基础
首先来看一个频繁集的性质。
定理:如果项目集X是频繁集,那么它的非空子集都是频繁集。
根据定理,已知一个k-频繁集的项集X,X的所有k-1阶子集都肯定是频繁集,也就肯定可以找到两个k-1频繁集的项集,它们只有一项不同,且连接后等于X。这证明了通过连接k-1频繁集产生的k-候选集覆盖了k-频繁集。同时,如果k-候选集中的项集Y,包含有某个k-1阶子集不属于k-1频繁集,那么Y就不可能是频繁集,应该从候选集中裁剪掉。Apriori算法就是利用了频繁集的这个性质。
三、算法步骤:
首先是测试数据:
|
交易ID |
商品ID列表 |
|
T100 |
I1,I2,I5 |
|
T200 |
I2,I4 |
|
T300 |
I2,I3 |
|
T400 |
I1,I2,I4 |
|
T500 |
I1,I3 |
|
T600 |
I2,I3 |
|
T700 |
I1,I3 |
|
T800 |
I1,I2,I3,I5 |
|
T900 |
I1,I2,I3 |
算法的步骤图:
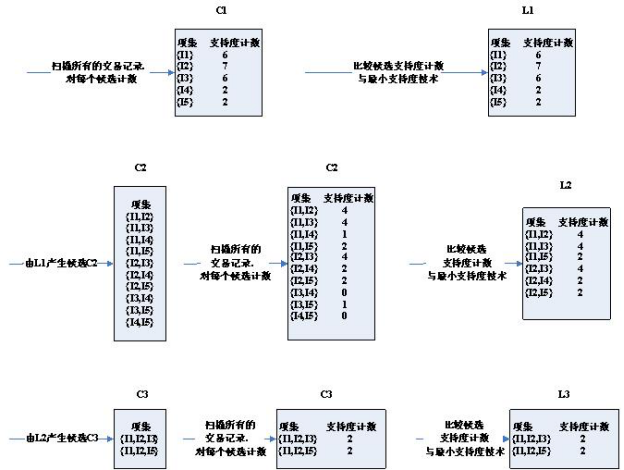
可以看到,第三轮的候选集发生了明显的缩小,这是为什么呢?
请注意取候选集的两个条件:
1.两个K项集能够连接的两个条件是,它们有K-1项是相同的。所以,(I2,I4)和(I3,I5)这种是不能够进行连接的。缩小了候选集。
2.如果一个项集是频繁集,那么它不存在不是子集的频繁集。比如(I1,I2)和(I1,I4)得到(I1,I2,I4),而(I1,I2,I4)存在子集(I1,I4)不是频繁集。缩小了候选集。
第三轮得到的2个候选集,正好支持度等于最小支持度。所以,都算入频繁集。
这时再看第四轮的候选集与频繁集结果为空
可以看到,候选集和频繁集居然为空了!因为通过第三轮得到的频繁集自连接得到{I1,I2,I3,I5},它拥有子集{I2,I3,I5},而{I2,I3,I5}不是频繁集,不满足:频繁集的子集也是频繁集这一条件,所以被剪枝剪掉了。所以整个算法终止,取最后一次计算得到的频繁集作为最终的频繁集结果:
也就是:['I1,I2,I3', 'I1,I2,I5']
四、代码:
编写Python代码实现Apriori算法。代码需要注意如下两点:
- 由于Apriori算法假定项集中的项是按字典序排序的,而集合本身是无序的,所以我们在必要时需要进行set和list的转换;
- 由于要使用字典(support_data)记录项集的支持度,需要用项集作为key,而可变集合无法作为字典的key,因此在合适时机应将项集转为固定集合frozenset。
def local_data(file_path): import pandas as pd dt = pd.read_excel(file_path) data = dt['con'] locdata = [] for i in data: locdata.append(str(i).split(",")) # print(locdata) # change to [[1,2,3],[1,2,3]] length = [] for i in locdata: length.append(len(i)) # 计算长度并存储 # print(length) ki = length[length.index(max(length))] # print(length[length.index(max(length))]) # length.index(max(length)读取最大值的位置,然后再定位取出最大值 return locdata,ki def create_C1(data_set): """ Create frequent candidate 1-itemset C1 by scaning data set. Args: data_set: A list of transactions. Each transaction contains several items. Returns: C1: A set which contains all frequent candidate 1-itemsets """ C1 = set() for t in data_set: for item in t: item_set = frozenset([item]) C1.add(item_set) return C1 def is_apriori(Ck_item, Lksub1): """ Judge whether a frequent candidate k-itemset satisfy Apriori property. Args: Ck_item: a frequent candidate k-itemset in Ck which contains all frequent candidate k-itemsets. Lksub1: Lk-1, a set which contains all frequent candidate (k-1)-itemsets. Returns: True: satisfying Apriori property. False: Not satisfying Apriori property. """ for item in Ck_item: sub_Ck = Ck_item - frozenset([item]) if sub_Ck not in Lksub1: return False return True def create_Ck(Lksub1, k): """ Create Ck, a set which contains all all frequent candidate k-itemsets by Lk-1's own connection operation. Args: Lksub1: Lk-1, a set which contains all frequent candidate (k-1)-itemsets. k: the item number of a frequent itemset. Return: Ck: a set which contains all all frequent candidate k-itemsets. """ Ck = set() len_Lksub1 = len(Lksub1) list_Lksub1 = list(Lksub1) for i in range(len_Lksub1): for j in range(1, len_Lksub1): l1 = list(list_Lksub1[i]) l2 = list(list_Lksub1[j]) l1.sort() l2.sort() if l1[0:k-2] == l2[0:k-2]: Ck_item = list_Lksub1[i] | list_Lksub1[j] # pruning if is_apriori(Ck_item, Lksub1): Ck.add(Ck_item) return Ck def generate_Lk_by_Ck(data_set, Ck, min_support, support_data): """ Generate Lk by executing a delete policy from Ck. Args: data_set: A list of transactions. Each transaction contains several items. Ck: A set which contains all all frequent candidate k-itemsets. min_support: The minimum support. support_data: A dictionary. The key is frequent itemset and the value is support. Returns: Lk: A set which contains all all frequent k-itemsets. """ Lk = set() item_count = {} for t in data_set: for item in Ck: if item.issubset(t): if item not in item_count: item_count[item] = 1 else: item_count[item] += 1 t_num = float(len(data_set)) for item in item_count: if (item_count[item] / t_num) >= min_support: Lk.add(item) support_data[item] = item_count[item] / t_num return Lk def generate_L(data_set, k, min_support): """ Generate all frequent itemsets. Args: data_set: A list of transactions. Each transaction contains several items. k: Maximum number of items for all frequent itemsets. min_support: The minimum support. Returns: L: The list of Lk. support_data: A dictionary. The key is frequent itemset and the value is support. """ support_data = {} C1 = create_C1(data_set) L1 = generate_Lk_by_Ck(data_set, C1, min_support, support_data) Lksub1 = L1.copy() L = [] L.append(Lksub1) for i in range(2, k+1): Ci = create_Ck(Lksub1, i) Li = generate_Lk_by_Ck(data_set, Ci, min_support, support_data) Lksub1 = Li.copy() L.append(Lksub1) return L, support_data def generate_big_rules(L, support_data, min_conf): """ Generate big rules from frequent itemsets. Args: L: The list of Lk. support_data: A dictionary. The key is frequent itemset and the value is support. min_conf: Minimal confidence. Returns: big_rule_list: A list which contains all big rules. Each big rule is represented as a 3-tuple. """ big_rule_list = [] sub_set_list = [] for i in range(0, len(L)): for freq_set in L[i]: for sub_set in sub_set_list: if sub_set.issubset(freq_set): conf = support_data[freq_set] / support_data[freq_set - sub_set] big_rule = (freq_set - sub_set, sub_set, conf) if conf >= min_conf and big_rule not in big_rule_list: # print freq_set-sub_set, " => ", sub_set, "conf: ", conf big_rule_list.append(big_rule) sub_set_list.append(freq_set) return big_rule_list if __name__ == "__main__": """ Test """ file_path = "test_aa.xlsx" data_set,k = local_data(file_path) L, support_data = generate_L(data_set, k, min_support=0.2) big_rules_list = generate_big_rules(L, support_data, min_conf=0.4) print(L) for Lk in L: if len(list(Lk)) == 0: break print("="*50) print("frequent " + str(len(list(Lk)[0])) + "-itemsets support") print("="*50) for freq_set in Lk: print(freq_set, support_data[freq_set]) print() print("Big Rules") for item in big_rules_list: print(item[0], "=>", item[1], "conf: ", item[2])
文件格式:
test_aa.xlsx
name con T1 2,3,5 T2 1,2,4 T3 3,5 T5 2,3,4 T6 2,3,5 T7 1,2,4 T8 3,5 T9 2,3,4 T10 1,2,3,4,5
参考相关博客:
http://blog.csdn.net/rongyongfeikai2/article/details/40457827
http://blog.csdn.net/opennaive/article/details/7051460
http://blog.csdn.net/opennaive/article/details/7047823
http://blog.csdn.net/androidlushangderen/article/details/43059211
代码参考