浅谈欧拉函数

欧拉函数是指对于正整数x，小于或等于x的数中与x互质的数的数量，通常用φ(x)表示。

我们先看一道例题

对题意进行分析，可以得到最小生成树中的两个直接连通的点的gcd一定是1，我们要统计最小生成树的个数，也就是求1~n每个数的欧拉函数值之和。

因此，对于一个正整数x，我们需要计算欧拉函数φ(x)。

1.求单个数的欧拉函数值

我们不妨通过几个简单的值推测一下。

①当x=1是，显然φ(x)=1

②当x为质数时，φ(x)=x-1

③当x可以写成p^k的形式时（x,k均为正整数），

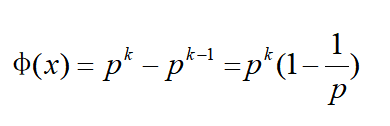
对于任意正整数x，我们将其分解质因数，如下图所示，得出欧拉函数的计算公式

因此，我们得出了求一个数的欧拉函数值的解法，时间复杂度为O(n√n).

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n;
ll ans;
int main() {
    scanf("%d", &n);
    ans = n;
    int maxx = sqrt(n);
    for (register int i = 2; i <= maxx; ++i) {
        if (n % i == 0) {
            ans = ans / i * (i - 1);
            while (n % i == 0) n /= i; 
        }
    }
    if (n > 1) ans = ans / n * (n - 1);
    printf("%lld
", ans);
    return 0;
}

2.线性筛求1~n每个数的欧拉函数值

众所周知，我们可以用线性筛在O(n)的时间内求出1~n的质数表。我们将该算法加以改造，便能在O(n)时间内求出任何积性函数的值，算法原理如下

引理：

①对于正整数i，当p为质数且p|i时，φ(i*p)=φ(i)*p

②对于正整数i，当p为质数且i%p!=0时，由积性函数的性质得φ(i*p)=φ(i)φ(p)=φ(i)*(p-1)

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n, vis[10010], prime[10010], num, f[10010];
int main() {
    scanf("%d", &n);
    for (register int i = 2; i <= n; ++i) {
        if (!vis[i]) {
            vis[i] = 1;
            prime[++num] = i;
            f[i] = i - 1;
        }
        for (register int j = 1; j <= num && i * prime[j] <= n; ++j) {
            vis[i * prime[j]] = 1;
            if (i % prime[j] == 0) {
                f[i * prime[j]] = f[i] * prime[j];
                break ;
            }
            else f[i * prime[j]] = f[i] * (prime[j] - 1);
        }
    }
    for (register int i = 1; i <= n; ++i) printf("%d ", f[i]);
    return 0;
}