hdu1799-循环多少次？-（组合恒等式）

循环多少次？

Time Limit: 3000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 6539    Accepted Submission(s): 2524

Problem Description

  我们知道，在编程中，我们时常需要考虑到时间复杂度，特别是对于循环的部分。例如，
如果代码中出现
for(i=1;i<=n;i++) OP ;
那么做了n次OP运算，如果代码中出现
fori=1;i<=n; i++)
  for(j=i+1;j<=n; j++) OP;
那么做了n*(n-1)/2 次OP 操作。
现在给你已知有m层for循环操作，且每次for中变量的起始值是上一个变量的起始值＋1（第一个变量的起始值是1），终止值都是一个输入的n，问最后OP有总共多少计算量。

 

Input

  有T组case，T<=10000。每个case有两个整数m和n，0<m<=2000，0<n<=2000.

 

Output

  对于每个case，输出一个值，表示总的计算量，也许这个数字很大，那么你只需要输出除1007留下的余数即可。

 

Sample Input

2 1 3 2 3

 

Sample Output

3 3

组合数公式：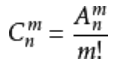

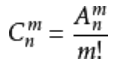
组合恒等式：C(n,m) = C(n-1,m) + C(n-1,m-1)

#include <iostream>
#include<stdio.h>
#include <algorithm>
#include<string.h>
#include<cstring>
#include<math.h>
#include<map>
#include<string>
#define inf 0x3f3f3f3f
#define ll long long
using namespace std;
int c[2001][2001];
const int p=1007;

void init()
{
    memset(c,0,sizeof(c));
    for(int i=0;i<2001;i++)
        c[i][0]=1;
    for(int i=1;i<2001;i++)
        for(int j=1;j<=i;j++)
            c[i][j]=( c[i-1][j-1]+c[i-1][j] )%p;
}
int main()
{
    init();
    int t;scanf("%d",&t);
    while(t--)
    {
        int n,m;
        scanf("%d%d",&m,&n);
        printf("%d
",c[n][m]);
    }
    return 0;
}