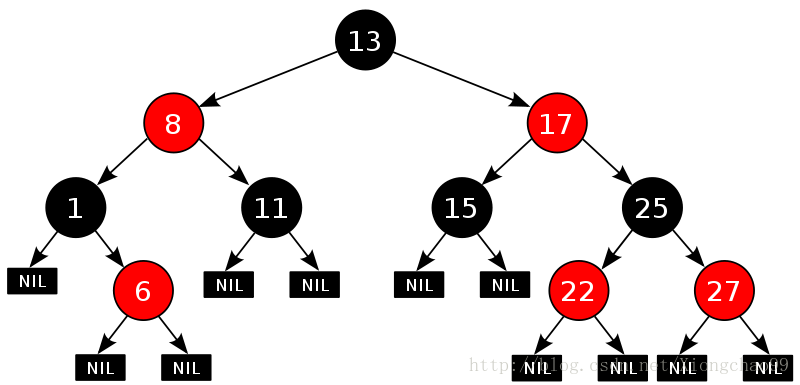
(1)红黑树来源于二叉搜索树,其在关联容器如map中应用广泛,主要优势在于其查找、删除、插入时间复杂度小,但其也有缺点,就是容易偏向一边而变成一个链表。
红黑树是一种二叉查找树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。也就是说,红黑树是在二叉
查找树基础上进一步实现的;
红黑树的五个性质:
性质1. 节点是红色或黑色;
性质2. 根节点是黑色;
性质3 每个叶节点(指树的末端的NIL指针节点或者空节点)是黑色的;
性质4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点);
性质5. 从任一节点到其每个尾端NIL节点或者NULL节点的所有路径都包含相同数目的黑色节点。
(注:上述第3、5点性质中所说的NIL或者NULL结点,并不包含数据,只充当树的路径结束的标志,即此叶结点非常见的叶子结点)。
因为一棵由n个结点随机构造的二叉查找树的高度为lgn,所以顺理成章,二叉查找树的一般操作的执行时间为O(lgn)。但二叉查
找树若退化成了一棵具有n个结点的线性链后,则这些操作最坏情况运行时间为O(n);
红黑树虽然本质上是一棵二叉查找树,但它在二叉查找树的基础上增加以上五个性质使得红黑树相对平衡,从而保证了
红黑树的查找、插入、删除的时间复杂度最坏为O(log n)。
(2)左旋右旋
红黑树插入或删除后,一般就会改变红黑树的特性,要恢复红黑树上述5个性质,一般都要那就要做2方面的工作:
1、部分结点颜色,重新着色
2、调整部分指针的指向,即左旋、右旋。
左选右旋如图所示:
左旋,如图所示(左->右),以x->y之间的链为“支轴”进行,使y成为该新子树的根,x成为y的左孩子,而y的左孩子则成为x的右孩
子。算法很简单,旋转后各个结点从左往右,仍然都是从小到大。
左旋代码实现,分三步:
(1) 开始变化,y的左孩子成为x的右孩子;
(2) y成为x的父结点;
(3) x成为y的左孩子;