PAT A1098 Insertion or Heap Sort (25分)(初始序列不参与是否与目标序列相同&&堆排序)

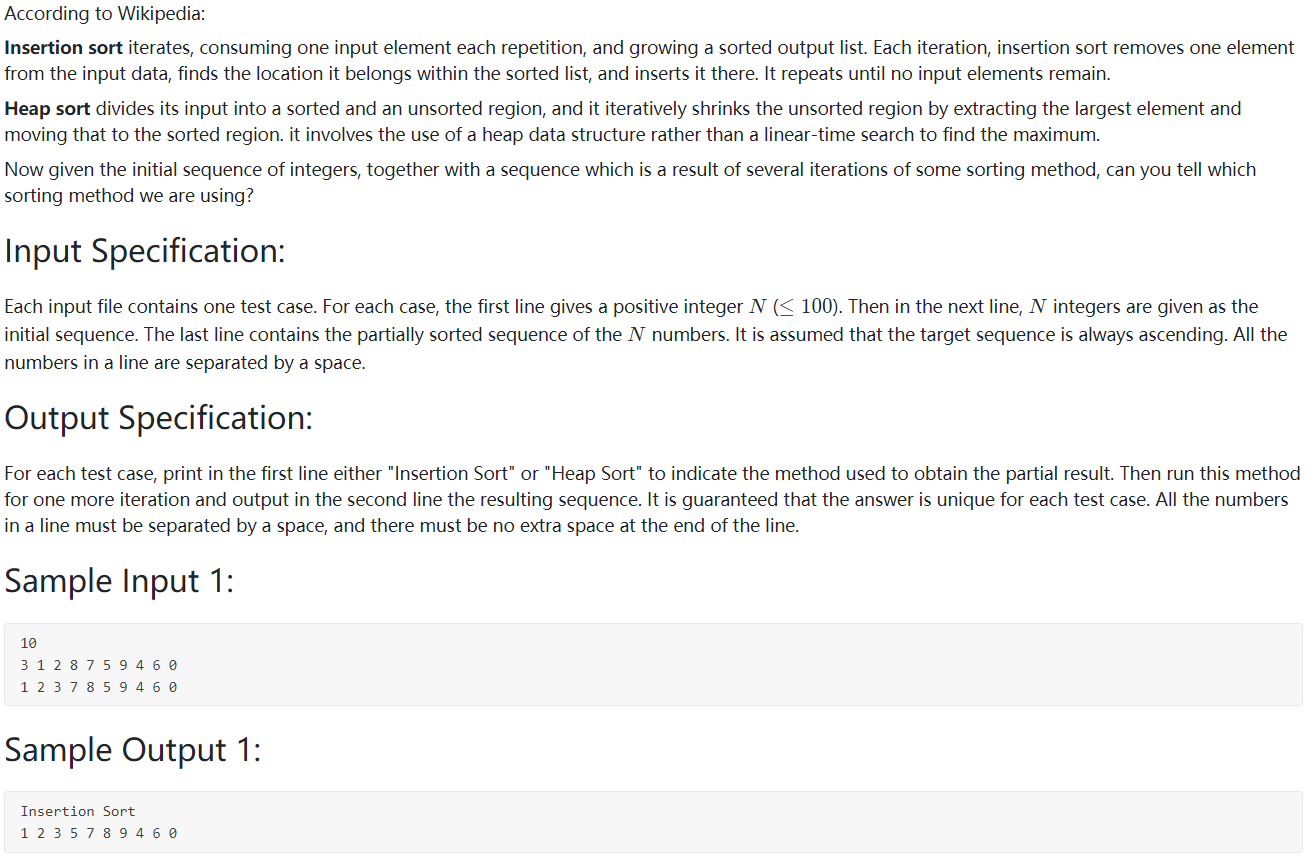
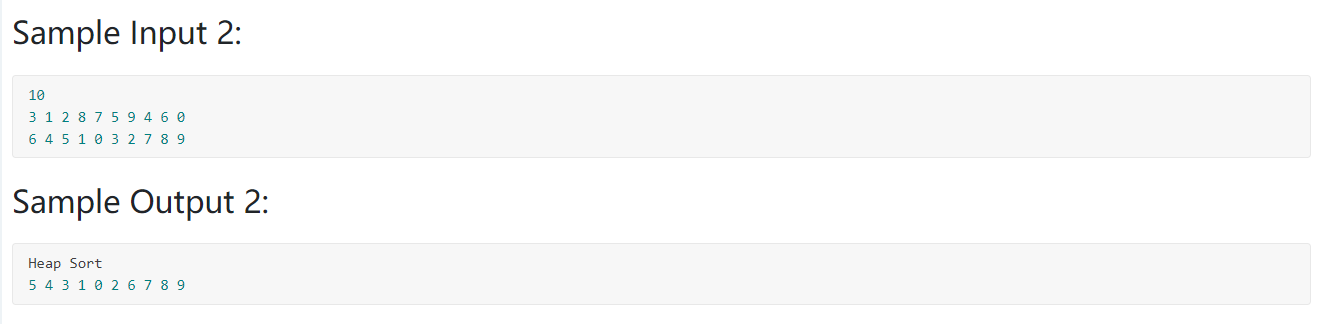
题目大意：给出n和n个数的序列a和b，a为原始序列，b为排序其中的一个步骤，问b是a经过了堆排序还是插入排序的，并且输出它的下一步～

分析：插入排序的特点是：b数组前面的顺序是从小到大的，后面的顺序不一定，但是一定和原序列的后面的顺序相同～所以只要遍历一下前面几位，遇到不是从小到大的时候，开始看b和a是不是对应位置的值相等，相等就说明是插入排序，否则就是堆排序啦～

插入排序的下一步就是把第一个不符合从小到大的顺序的那个元素插入到前面已排序的里面的合适的位置，那么只要对前几个已排序的+后面一位这个序列sort排序即可～while(p <= n && b[p - 1] <= b[p]) p++；int index = p；找到第一个不满足条件的下标p并且赋值给index，b数组下标从1开始，所以插入排序的下一步就是sort(b.begin() + 1, b.begin() + index + 1)后的b数组～

堆排序的特点是后面是从小到大的，前面的顺序不一定，又因为是从小到大排列，堆排序之前堆为大顶堆，前面未排序的序列的最大值为b[1]，那么就可以从n开始往前找，找第一个小于等于b[1]的数字b[p]（while(p > 2 && b[p] >= b[1]) p--；），把它和第一个数字交换（swap(b[1], b[p])；），然后把数组b在1~p-1区间进行一次向下调整（downAdjust(b, 1, p - 1)；）～向下调整，low和high是需要调整的区间，因为是大顶堆，就是不断比较当前结点和自己的孩子结点哪个大，如果孩子大就把孩子结点和自己交换，然后再不断调整直到到达区间的最大值不能再继续了为止～

#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
const int N = 110;
vector<int> list,target,temp;
int n;

bool insertsort(){
    temp = list;
    for(int i = 1;i<n;i++){
        sort(temp.begin(),temp.begin()+i);
        if(i!=1&&temp==target){
            sort(temp.begin(),temp.begin()+i+1);
            return true;
        }
    }
    return false;
    
}
void downadjust(int low,int high){
    int i  = low,j = 2*i+1;
    while(j<=high){
        if(j+1<=high&&temp[j+1]>temp[j]){
            j = j+1;
        }
        if(temp[j]>temp[i]){
            swap(temp[j],temp[i]);
            i = j;
            j = 2*i+1;
        }else{
            break;
        }
    }
    
}

bool heapsort(){
    temp = list;
    for(int i = n/2;i>=0;i--){
        downadjust(i,n-1);
    }
    for(int i  = n-1;i>0;i--){
        if(i!=n-1&&temp==target){
           swap(temp[i],temp[0]);
            downadjust(0,i-1);
            return true;
        }
        swap(temp[i],temp[0]);
        downadjust(0,i-1);
    }
    return false;
}
int main(){
    scanf("%d",&n);
    for(int i = 0;i<n;i++){
        int num;
        scanf("%d",&num);
        list.push_back(num);
    }
    for(int i = 0;i<n;i++){
        int num;
        scanf("%d",&num);
        target.push_back(num);
    }    
    //insertsort
    if(insertsort()==true){
        printf("Insertion Sort
");
        for(int i = 0;i<n;i++){
            printf("%d",temp[i]);
            if(i!=n-1) printf(" ");
        }
    }else if(heapsort()==true){
        printf("Heap Sort
");
        for(int i = 0;i<n;i++){
            printf("%d",temp[i]);
            if(i!=n-1) printf(" ");
        }        
    }
    return 0;
}