题目大意
给一个无根树,可以给任意一条边赋值,要求任意两个叶子节点间的简单路径的权值异或之和都相等, 问最多与最少用几个数字。
分析
最多的情况
因为任意两个叶子节点间的简单路径的权值异或之和都相等,所以对于一个直接连接着若干个叶子的结点的一个(LCA)来说,很显然其所有叶子节点所连的边的权值只能是一种。而对于不是与叶子节点直接相连的(LCA)来说,其简单路径上的边权都可以取不同的值。
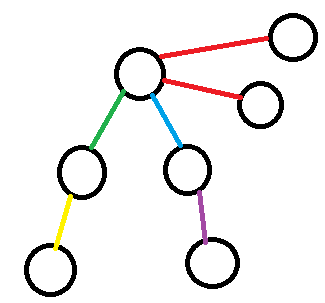
两个红边相连的叶子因为只有一条边与公共节点相连所以一定是相等的。而对于另外两个叶子节点,一定能找到(4)个不同的数,使它们到公共节点的异或和相等。所以说最多的情况就是边数减去每个(LCA)与其直接相连的叶子节点数的总值减去一的值。(比如图中两条红色边算一条)。
最少的情况
由上面的分析可得,所有叶子节点到(LCA)的异或和可以都相等,所以可以简化为一个叶子节点,然后整个图就简化成了这个样子(官方题解的图):

如果所有的叶子直接的简单路径距离都是偶数的话,直接把所有边的权值设成相等就行了。如果有一个叶子节点到另一个叶子节点的简单路径距离是奇数的话,就按图中的样子,每个叶子节点的值都是其到根结点的异或和就行了。
所以说最少只有两种情况(1)(所有叶子节点的简单路径长度都是偶数)否则就是(3)。
具体实现
对于最多的情况,我们只要计算一下(n)减去每个结点所直接相连的叶子节点的数量减一后的值就行了(如果没有不用减)。对于最少的情况,需要判断任意两个叶子节点的简单距离是否为奇数,这个可以通过黑白染色来解决。本题参考了狗哥的视频,欢迎大家去给(up)主一键三连(笑)。
代码
const int maxn = 1e5+10;
vector<int> e[maxn];
bool flag;
void dfs(int p, int u, bool c) {
if (e[u].size()==1) {
if (!c) flag = true;
}
for (auto v : e[u])
if (v!=p) dfs(u, v, !c);
}
int main(void) {
IOS; int n;
while(cin>>n) {
for (int i = 1, u, v; i<n; ++i) {
cin >> u >> v;
e[u].push_back(v);
e[v].push_back(u);
}
flag = false;
for (int i = 1; i<=n; ++i)
if (e[i].size()==1) {
dfs(-1, i, true); //随便找个叶子做根结点
break;
}
int minn = flag ? 3 : 1; //判断是否有和根结点颜色不一样的点
int maxx = n-1;
for (int i = 1; i<=n; ++i) {
int cnt = 0;
if (e[i].size()!=1)
for (auto v : e[i])
if (e[v].size()==1) ++cnt;
if (cnt) maxx -= cnt-1;
}
for (int i = 1; i<=n; ++i) e[i].clear();
cout << minn << ' ' << maxx << endl;
}
return 0;
}