题目大意
给你一棵树,让你找出树上的三个不同的点,使得它们之间的简单路径包含的边最多。
分析
先说结论,选出的三个点必定有两个点是树的直径上的两个端点,如果给出的树是一条链,结论必定成立,下面是给出的树不是链的时候的证明。
设三个点分别为a,b,c,设每条边的边权为1,那么答案就是dis(a,b)+dis(a,c)+dis(b,c)。如果给出的树不是一条链,那么a,b,c三点之间必然由一个点连接,设这个点为点d。
1.首先其中一个点一定是离点d最远的点,否则肯定不是最优解。然后这个点必定可以是树的直径上的一个端点(命题1),下面的证明不考虑等于的情况,因为等于的话,命题显然是成立的。
我们首先找一个点作为根节点,把无根树变成有根树,得到下面的树(为了作图方便省略部分任意两个节点与其lca之间的点,注意,叶子节点没有被省略)。
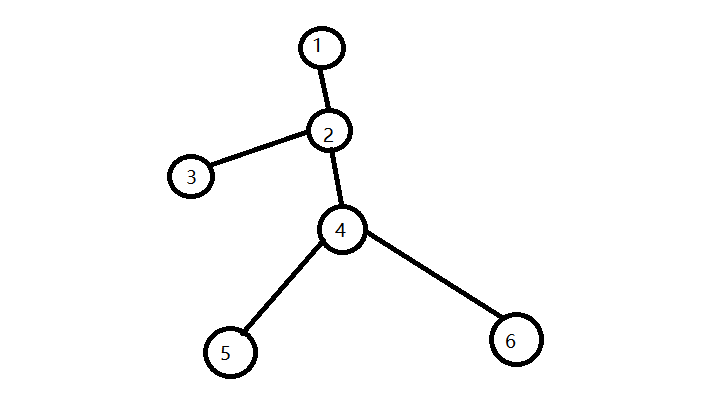
假设命题1不成立,设点2,点3是树的直径上的点,而点4,5是最优解的路径中包含的点,并且他们不是树的直径上。由树的直径的定义可知,dis(2,3)大于dis(4,5),点4,5不是最优解的路径中包含的点,与前面矛盾,所以命题1成立。
此时,还有一种情况,设点2,点3是最优解的路径中包含的点,并且他们不在树的直径上,而点4,5是树的直径上的点。可以得到dis(2,3)大于dis(2,5),易得,dis(3,4)大于dis(4,5),从而得到点4,5不是树的直径上的点,与前面矛盾,所以命题1成立。
2.我们再证第二个点也是树的直径上的一个点。其实,我们只要证:点d必定是树的直径上的一个点(命题2)就行了。
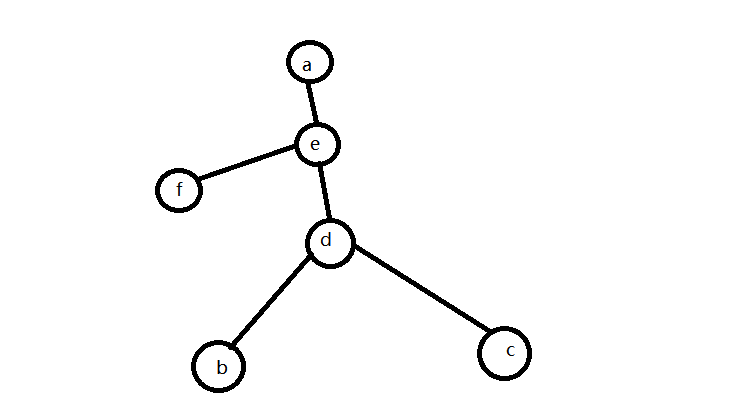
假设点a是树的直径上的一个端点,d点不是树的直径上的点,e点是树的直径上的一个点,f点是离e点最远的点(显然,它是树的直径的一个端点)。此时,点b,点c一定是离点d最远的点,否则不是最优解。如果此时将连接点从点d换成点e,那么点b或者点c就会变成点f,而还需要经过点d这个点,最终的结果会减去dis(b,d),加上dis(e,f),因为点a是树的直径上的一个端点,所以dis(a,f)大于dis(a,d),易得dis(e,f)大于dis(d,b),更换连接点后答案更优,所以命题2成立。
做法就很简单了,求出树的直径之后枚举出距离两个直径端点距离之和最远的点就行了。
具体实现
可以先跑一个(dfs),求树的直径的第一个端点(a),然后再以(a)点为根跑(dfs)得到另外一个端点(b),以及所有点到(a)的距离,最后跑一遍(dfs)求所有点到(b)的距离。这样处理之后,我们枚举所有与(a)和(b)不同的点找一个到这两个点最远的点就行了。
代码
const int maxn = 2e5+10;
vector<int> e[maxn];
int disx[maxn] = {-1}, disy[maxn] = {-1}, tmp;
void dfs(int p, int u, int *dis) {
dis[u] = dis[p]+1;
for (auto v : e[u])
if (v != p) dfs(u, v, dis);
if (dis[tmp]<dis[u]) tmp = u;
}
int main(void) {
int n;
scanf("%d", &n);
for (int i = 0, u, v; i<n-1; ++i) {
scanf("%d%d", &u, &v);
e[u].push_back(v);
e[v].push_back(u);
}
dfs(0, 1, disy); int x = tmp; tmp = x;
dfs(0, x, disx); int y = tmp;
dfs(0, y, disy);
int z, sum = 0;
for (int i = 1; i<=n; ++i)
if (sum<disx[y]+disx[i]+disy[i] && i!=x && i!=y) {
z = i;
sum = disx[y]+disx[i]+disy[i];
}
printf("%d
%d %d %d
", sum/2, x, y, z);
return 0;
}