欧拉回路

参考这里及百度百科

欧拉回路的判断：

在图为连通图的前提下

无向图：所有顶点的度都为偶数（这个不判断联通也行。。）

有向图：所有顶点的入读等于出度。

只要理解一个点有进就有出就可以了。

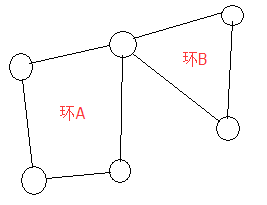
欧拉路径的判断：

首先图要连通。

无向图：有且仅有两个点的度为奇数，其实就是上面欧拉回路少一条边。

有向图：最多有一个点的入度等于出度 + 1， 最多有一个点的出度等于入度 + 1.

给个欧拉路径的图

HDU1116

这个要先用判断图是否连通

#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <cmath>
#include <sstream>
#include <algorithm>
#include <set>
#include <map>
#include <vector>
#include <queue>
#include <iomanip>
#include <stack>

using namespace std;

typedef long long LL;
const int INF = 0x3f3f3f3f;
const int MAXN = 100005;
const int MOD = 20180812;

#define MemI(x) memset(x, -1, sizeof(x))
#define Mem0(x) memset(x, 0, sizeof(x))
#define MemM(x) memset(x, 0x3f, sizeof(x))

int fa[205], in[205], out[205], book[205];
int Find(int a)
{
    if(fa[a] == a)
        return a;
    return fa[a] = Find(fa[a]);
}

void Mix(int a, int b)
{
    int x = Find(a), y = Find(b);
    if(x != y)
        fa[y] = x;
}

int main()
{
    int T;
    cin >> T;
    while(T--)
    {
        Mem0(in);
        Mem0(out);
        Mem0(book);
        for(int i = 'a';i <= 'z';++i)
            fa[i] = i;
        int n;
        cin >> n;
        string s;
        for(int i = 0;i < n;++i)
        {
            cin >> s;
            in[s[0]]++, out[s[s.size() - 1]]++;
            book[s[0]] = book[s[s.size() - 1]] = 1;
            Mix(s[0], s[s.size() - 1]);
        }
        int num = 0;
        for(int i = 'a';i <= 'z';++i)
        {
            if(book[i] && fa[i] == i)
                num++;
        }
        if(num > 1)
            cout << "The door cannot be opened." << endl;
        else
        {
            int flag1 = 0, flag2 = 0;
            for(int i = 'a';i <= 'z';++i)
            {
                if(in[i] == out [i] + 1)
                    flag1++;
                else if(in[i] + 1== out[i])
                    flag2++;
                else if(in[i] > out[i] || out[i] > in[i])
                    flag1 = flag2 = 2;
            }
            if(flag1 > 1 || flag2 > 1)
                cout <<  "The door cannot be opened." << endl;
            else
                cout << "Ordering is possible." << endl;
        }
    }
    return 0;
}

输出欧拉路径，网上很多方法，这里挑了个容易写的

stack<int> s;
void dfs(int x)
{
    s.push(x);
    for(int i = 0;i < n;++i)
    {
        if(mp[x][i])
        {
            mp[x][i] = mp[i][x] = 0;
            dfs(i);
            break;
        }
    }
}