【补】[LCA]倍增版LCA

咕咕咕
blog密码差点忘了
NOIP之前坑还是要填的
之后。。肯能就退役了wwwww

LCA

众所周知， LCA有许多的求法（比如暴力）
对于一个静态的图，我们可以用RMQ,倍增等解决
好像动态图能用LCT做？？？

先说倍增

倍增，意思是成倍的增加增长；成倍地增长。（来源：百度百科）
像ST表一样，用一个数组下标表示 (2^j) 步后的父亲节点是什么

怎么用来求LCA？

先来说说任意两个节点的位置关系和他们的LCA的关系

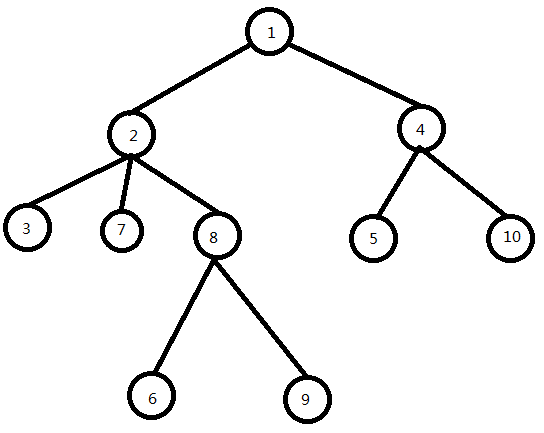
先来简单的:3和10(同深度，LCA为根节点)

可以直接看出LCA为1
通过前面倍增记录的父亲节点不断向上跳，跳到相同时出现LCA

但是事情是不会这样简单的——鲁迅

6和9(同深度，LCA不是根节点)

这次也可以直接看出LCA为8
然而可以跳到两者相同吗？？
并不能，因为那样跳很容易会跳到2，而且不确定能否回去
所以我们要跳到两者最后不同的父节点上，查出任意一个的父节点得到答案

5和9（深度不同）

只有深度相同的时候我们才能一起往上跳，所以现将较深的点向上跳到一样深度的时候再做第二条

2和9（LCA为其中一个点）

这次我们在将较深的点往上跳的时候会发现两个点重合了，所以要在一起往上跳之前判断是否在一个点上

代码(luoguP3379)

#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const int MAXN=7500011;
const int MLOG=log2(7500000)+1;
int fa[MAXN][30];
int dep[MAXN];
struct EDGE {
	int v,nxt;
}edge[MAXN];
int head[MAXN];
int ecnt;
void addedge(int u,int v) {
	edge[++ecnt].nxt=head[u];
	edge[ecnt].v=v;
	head[u]=ecnt;
}
void dfs(int u,int nowdep) {
	dep[u]=nowdep;
	for(int i=head[u]; i; i=edge[i].nxt) {
		int v=edge[i].v;
		if(!dep[v]) {
			fa[v][0]=u;
			dfs(v,nowdep+1);
		}
	}
}

int LCA(int a,int b) {
	if(dep[a]<dep[b])swap(a,b);
	for(int j=MLOG; j>=0; j--) {
		if(dep[a]-(1<<j)>=dep[b])a=fa[a][j];
	}
	if(a!=b) {
		for(int j=MLOG; j>=0; j--) {
			if(fa[a][j]!=fa[b][j]) {
				a=fa[a][j];
				b=fa[b][j];
			}
		}
		a=fa[a][0];
	}
	return a;
}

int main() {
	int n,m,s;
	scanf("%d %d %d",&n,&m,&s);
	for(int i=1; i<n; i++) {
		int u,v;
		scanf("%d %d",&u,&v);
		addedge(u,v);
		addedge(v,u);
	}
	dfs(s,1);
	for(int j=1; j<=MLOG; j++) {
		for(int i=1; i<=n; i++) {
			fa[i][j]=fa[fa[i][j-1]][j-1];
		}
	}
	for(int i=1; i<=m; i++) {
		int x,y;
		scanf("%d %d",&x,&y);
		printf("%d
",LCA(x,y));
	}
	return 0;
}