ZOJ 3728 Collision

---恢复内容开始---

今天无事水一水，结果就看到这个水题了！

题意思是 有俩个区域如图

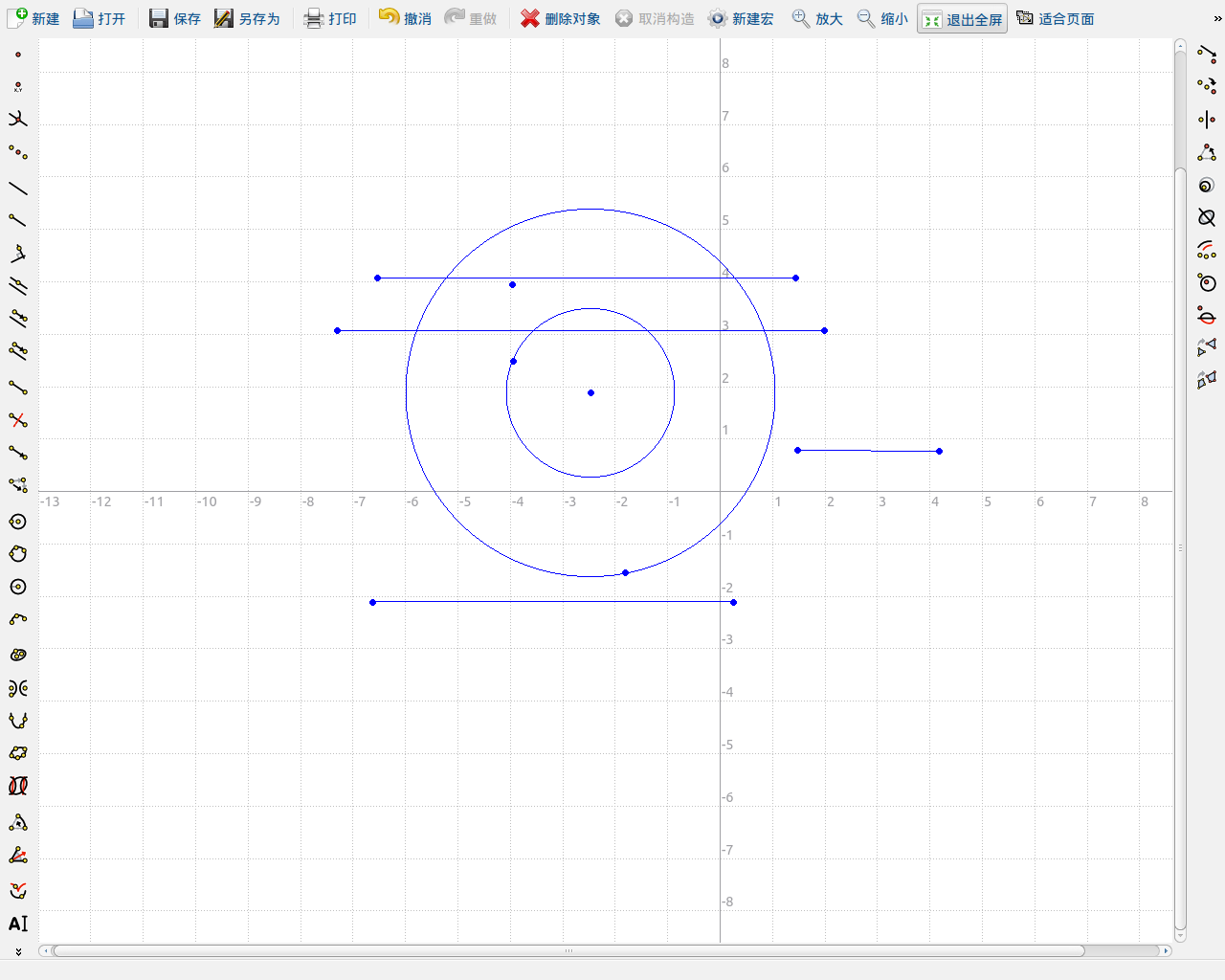
求在俩个圆之间的运动时间 给出 初始的开始点和速度的矢量式;而且这个点 不再俩个圆之间的区域，且碰到内测园会反弹：

在大大物实验的时候记得学过为了减少误差 和简易计算可以:把这个小圆看成质点，并把固定园的半径加上小圆的半径。

　　其实就是求 与俩个圆与射线的交点！ 代码如下：（）

　　

#include <cstring>
#include <cmath>
#include <algorithm>
#include <cstdlib>
#include <cstdio>
using namespace std;
struct point
{
    double x,y;
    point (double x=0,double y=0):x(x),y(y){}
};
typedef point Vector;
const double eps=1e-8;
int dcmp(double x)
{
    if(fabs(x)<eps) return 0;
    return x<0?-1:1;
}
Vector operator + (Vector a,Vector b){return Vector(a.x+b.x,a.y+b.y);}
Vector operator - (Vector a,Vector b){return Vector(a.x-b.x,a.y-b.y);}
Vector operator * (Vector a,double b){return Vector(a.x*b,a.y*b);}

double det(Vector a,Vector b){return a.x*b.y-a.y*b.x;}
double dot(Vector a,Vector b){return a.x*b.x+a.y*b.y;}
double lenth(Vector a){return sqrt(dot(a,a));}
struct line
{
    point p;
    Vector v;
    double angle;
    line(){}
    line(point p,Vector v):p(p),v(v){}
    bool operator <(const line &rht)const
    {
        return angle<rht.angle;
    }
};
struct circle
{
    point c;
    double r;
    circle(){c=point(0.0,0.0);}
    circle(point c,double r):c(c),r(r){}
    point Point(double rad)
    {
        return point(c.x+cos(rad)*r,c.y+sin(rad)*r);
    }
};
int get_circle_intersection(line L,circle C,double &t1,double &t2)
{
    t1=t2=0;
    double a=L.v.x, b=L.p.x-C.c.x,c=L.v.y,d=L.p.y-C.c.y;

    double e=a*a+c*c,f=2*(a*b+c*d),g=b*b+d*d-C.r*C.r;

    double detle = f*f-4*e*g;

    if(dcmp(detle)<0) return 0;
    if(dcmp(detle)==0) {t1=t2=-f/(2*e);return 1;}
    t1=(-f-sqrt(detle)) /(2*e);
    t2=(-f+sqrt(detle)) /(2*e);
    if(dcmp(t1)<0 || dcmp(t2)<0) return 0;//按照速度的反方向才可以和圆相交
    return 2;
}
int main()
{
    double t1,t2;
    double x1,x2;
    line tmp;
    circle tmp1;
    circle tmp2;
    double Rm, R, r;
    while(~scanf("%lf %lf %lf %lf %lf %lf %lf",&Rm,&R,&r,&tmp.p.x,&tmp.p.y,&tmp.v.x,&tmp.v.y))
    {
        Rm+=r;R+=r;
        tmp1.r=Rm;
        tmp2.r=R;
        int count1=get_circle_intersection(tmp,tmp1,t1,t2);
        int count2=get_circle_intersection(tmp,tmp2,x1,x2);
        if(count2==0)printf("0.00
");
        else
            printf("%.3lf
",fabs(x2-x1)-fabs(t1-t2));// 因为直线式点+向量（和速度一样）所以减法就可以了
    }
    return 0;
}