这俩个题 题意::给出N(<1e5)个点求找到一个点作为聚会的地方,使每个点到达这里的距离最小。4311是 曼哈顿距离 4312是 切比雪夫距离;
曼哈顿距离 :大家都知道 对于二维坐标系a(xa,yb),b(xb,yb)的曼哈顿距离是abs(xa-xb)+abs(ya-yb);
看的出来这个距离和x,y 都有关,但是X,Y并不相互影响,所以可以分开计算这样,分开计算的好处如下:
如果 只给一个维度的坐标系 ,我们是不可以再什么养的复杂度的时间内处理出来呢? 大难还是很好想的先排序一下,会发现就需要O(n)的时间就可以算出来我们想要的答案
至于俩个维度的合并运算只要O(N)记录就可以了;
切比雪夫距离:
我们知道对于距离一个点的曼哈顿距离为R 的点可以形成一个正方形如下图:
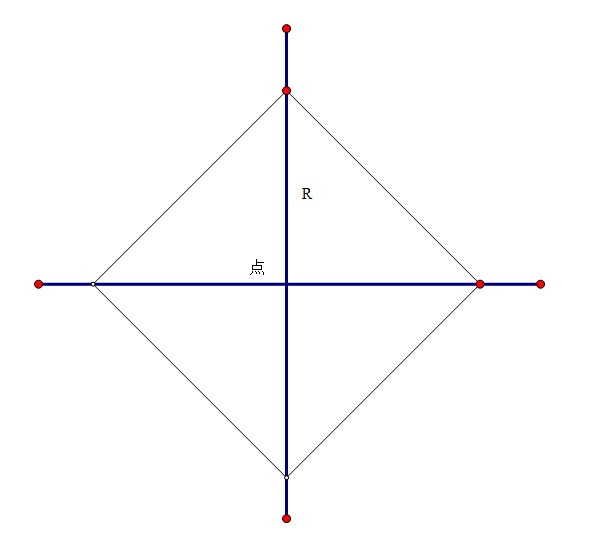
也知道对于距离一个点的切比雪夫距离为R 的点也可以形成一个正方形如下图:
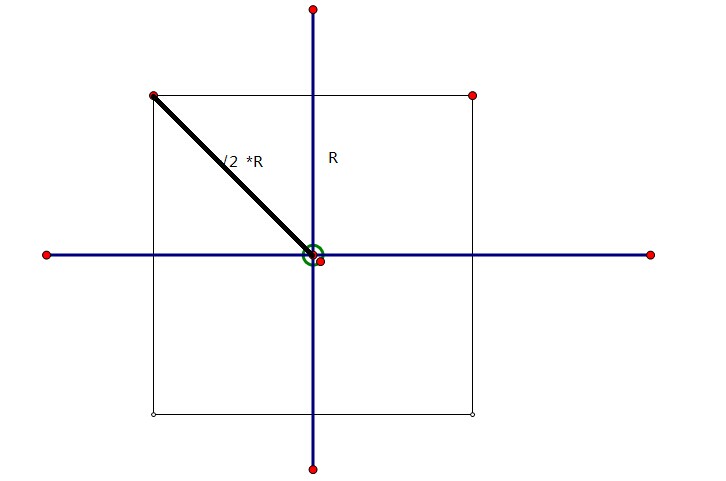
对比俩个图片我们知道:距离一个点的 切比雪夫距离可以通过一定的变换转换成 曼哈顿距离(因为曼哈顿距离怎么算我们上面已经讲过了)!!!;
比较麻烦?:但其实很简单:我们知道上面的 切比雪夫的正方形 旋转45度 在变换一定的倍数会 和 曼哈顿的正方形重合!所以我饿们可以认为 切比雪夫距离是 曼哈顿距离旋转在放大的结果:反过来只要对坐标进行同样的旋转和放大就可以了;
代码如下:::
#include <cstdio> #include <map> #include <vector> #include <set> #include <iostream> using namespace std; typedef long long LL; struct info { LL x,y; int cnt; info(){} info(int x,int y):x(x),y(y){} }; bool cmpx(info a,info b) { if(a.x==b.x)return a.y<b.y; return a.x<b.x; } bool cmpy(info a,info b) { if(a.y==b.y) return a.x<b.x; return a.y<b.y; } info ko1[100005]; info ko2[100005]; LL dp1[100005]; LL dp2[100005]; int n; void make(int x) { int tmpx,tmpy; tmpx=ko1[x].x; tmpy=ko1[x].y; //这么写是按远点点进行逆时针旋转的 //你也可以按别的点进行旋转 不过们的旋转点必须是一个 //列 //tmpx=ko1[x].x-2; //tmpy=ko1[x].y+12; ko1[x].x=tmpx-tmpy; ko1[x].y=tmpy+tmpx; } int main() { int t; scanf("%d",&t); while(t--) { scanf("%d",&n); for(int i=1;i<=n;i++) { // cin>>ko1[i].x>>ko1[i].y; scanf("%I64d%I64d",&ko1[i].x,&ko1[i].y); make(i);//有这句是12 没这句是11 } sort(ko1+1,ko1+1+n,cmpx); for(int i=1;i<=n;i++) { ko1[i].cnt=i; ko2[i]=ko1[i]; } sort(ko2+1,ko2+1+n,cmpy); for(int i=1;i<=n;i++) { dp1[i]=dp1[i-1]+abs(ko1[i].x-ko1[1].x); dp2[i]=dp2[i-1]+abs(ko2[i].y-ko2[1].y); } LL ans=1LL<<62; for(int i=1;i<=n;i++) { LL tmp2=dp2[n]-dp2[i]-(ko2[i].y-ko2[1].y)*(n-i)+(ko2[i].y-ko2[1].y)*i-dp2[i]; int cnt=ko2[i].cnt; LL tmp1=dp1[n]-dp1[cnt]-(ko1[cnt].x-ko1[1].x)*(n-cnt)+(ko1[cnt].x-ko1[1].x)*cnt-dp1[cnt]; ans=min(ans,(tmp1+tmp2)/2);// 这个12 要除以2;11不需要 } cout<<ans<<endl; } return 0; }