51nod1275（单调队列）

1275 连续子段的差异

题意：

　　给出一个序列，定义最大值与最小值之差不超过k的子区间为合法子区间，问一个序列有多少合法子区间。

分析：

　　首先考虑最简单的情况，如果整个区间合法，那么一个有2^n-1个合法子区间。其次需要知道的是，所有区间长度为1的子区间全部合法。然后对于每个点找到的最大可行区间，与前一个点对应的可行区间有两种关系：后者包括前者，后者与前者有交集（不考虑可行区间为自己的）。对于前者，如果以 i 为右端点的最大可行区间的左端点是 l，那么【l，i-1】区间也一定是合法的，因为根据题意一个区间合法，它的子区间肯定合法。对于后者，如果 i 刚好是可行区间的最大值，当我们考虑以i-1为右端点时，就有可能它的左端点还能向左延伸。

　　1.对于第一种情况，如果一段最大可行区间为【l，r】，那么我们一定也会得到【l，l】，【l，l+1】，【l，l+2】……【l，r】，对于这些区间其实我们只要计算的就是【l，r】所能形成的子区间的个数，因为一开始就计算了长度为1的子区间的个数，所以这里我们只需考虑长度大于等于2的子区间的个数。len=2，num=（r-l+1）-1；len=3，num=（r-l+1）-2（len为子区间的长度，num为长度为len的子区间的个数）……所以总和就是1+2+3+……+（r-l），然后我们发现总和其实就是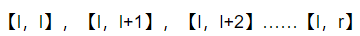这些子区间的长度-1相加的和。

　　2.对于第二种情况，假设前者的可行区间为【l1，r1】，后者的可行区间为【l2，r2】，一定满足r2=r1+1。这里可以简单证明一下，如果r2=r1+n（n>1）,因为【l2，r1+n】合法，那么【l2,r1+1】，【l2，r2+2】……【l2，r2+n】也一定是合法的。而我们枚举是是从左往右把每个 i 值当作可行区间的右边界，那么我们一定会先遇到【l2，r1+1】，也就是说一定是r2=r1+1的。对于有些子区间我们已经在之前区间计算过了，就不需要重复计算，考虑到该区间只多出一个新元素，很容易想到我们没有计算的子区间就是包含了这个新元素的区间，不难看出该区间包含这个新元素的子区间的个数为长度-1个。

　　综上，对于每个可行区间我们都是加上他们的长度-1，所以最后有效子区间的个数就是所有可行区间的长度减1的和，再加上长度为1的子区间的个数。

　　对于确定的右边界求最大可行区间，用两个单调队列维护区间最大值和最小值，通过调节子区间的最大值和最小值，找到左边界就好了。

代码：

#include <stack>
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>

using namespace std;
#define ll long long
#define ull unsigned long long
#define cls(x) memset(x,0,sizeof(x))
#define clslow(x) memset(x,-1,sizeof(x))

const int maxn=1e5+100;

int n,k,ans;

int a[maxn];
int que1[maxn],que2[maxn];

void solve()
{
    //pos记录可行区间的左边界
    int pos=1;
    int head1=0,rear1=0,head2=0,rear2=0;
    for(int i=1;i<=n;i++){
        while(rear1>head1&&a[que1[rear1-1]]>a[i])   rear1--;
        while(rear2>head2&&a[que2[rear2-1]]<a[i])   rear2--;
        //单调递增区间，维护最小值
        que1[rear1++]=i;
        //单调递减区间，维护最大值
        que2[rear2++]=i;

        //找到最左可行区间
        while(rear1>head1&&rear2>head2&&a[que2[head2]]-a[que1[head1]]>k){
            //跳出循环时,pos不会被赋值，所以需要在循环里+1
            if(que2[head2]>que1[head1]) pos=que1[head1++]+1;
            else                        pos=que2[head2++]+1;
        }
        if(rear1>head1&&rear2>head2){
            ans+=i-pos;
        }
    }
}

int main()
{
//    freopen("in.txt","r",stdin);
    while(scanf("%d%d",&n,&k)!=EOF)
    {
        ans=n;
        for(int i=1;i<=n;i++){
            scanf("%d",&a[i]);
        }

        solve();
        printf("%d
",ans);
    }
    return 0;
}