hdu1695（莫比乌斯）

GCD

题意：

　　从【a，b】和【c，d】区间分别挑选一个整数x，y，满足gcd（x，y）= k的数对个数。（不考虑x，y顺序且保证a，c为1）

分析：

　　不难看出该题可以转换为求【a，b/k】和【c，d/k】中gcd（x，y）= 1的数对个数，然后根据莫比乌斯函数

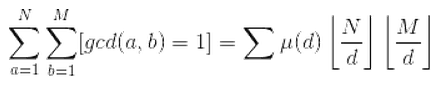
求出数对的个数即可。需要注意的是题目中不考虑数对的顺序，所以我们要对结果去重。考虑到结果中重复的部分为【a，min（b/k，d/k）】和【c，min（b/k，d/k）】区间满足条件的数对，所以我们对这两个区间求一下数对个数，结果除以2即是重复的个数。

　　参考博客：大佬博客

代码：

#include <queue>
#include <vector>
#include <math.h>
#include <string>
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>

using namespace std;
#define ll long long
#define ull unsigned long long
#define cls(x) memset(x,0,sizeof(x))
#define clslow(x) memset(x,-1,sizeof(x))

const int maxn=1e5+100;

int a,b,c,d,k,T;

bool check[maxn];
int prime[maxn],mu[maxn];

void Moblus(int n)
{
    mu[1]=1;
    int tot=0;
    cls(check);
    for(int i=2;i<=n;i++){
        if(!check[i]){
            prime[tot++]=i;
            mu[i]=-1;
        }
        for(int j=0;j<tot;j++){
            if(i*prime[j]>n) break;
            check[i*prime[j]]=true;
            if(i%prime[j]==0){
                mu[i*prime[j]]=0;
                break;
            }
            else {
                mu[i*prime[j]]=-mu[i];
            }
        }
    }
}

int main()
{
    #ifndef ONLINE_JUDGE
        freopen("in.txt","r",stdin);
    #endif // ONLINE_JUDGE
    scanf("%d",&T);
    for(int kase=1;kase<=T;kase++){
        scanf("%d %d %d %d %d",&a,&b,&c,&d,&k);
        if(k==0){
            printf("Case %d: 0
",kase);
            continue;
        }
        b/=k;d/=k;
        if(b>d) swap(b,d);
        Moblus(b);
        ll ans=0,res=0;
        for(int i=1;i<=b;i++){
            ans+=(ll)mu[i]*(b/i)*(d/i);
            res+=(ll)mu[i]*(b/i)*(b/i);
        }
        printf("Case %d: %lld
",kase,ans-res/2);
    }
    return 0;
}