$Matrix-Tree$
其实矩阵树的题挺好玩的,一些是套班子求答案的,也有一些题目是靠观察基尔霍夫矩阵性质推式子的。
文艺计算姬:https://www.lydsy.com/JudgeOnline/problem.php?id=4766
题意概述:求完全二分图的生成树数目。左部点的个数为n,右部为m,答案对p取模。$n,m,p<=10^{18}$
好玩的题目!刚看到这个题的时候以为是一道板子题,看了一眼数据范围...对于完全二分图,基尔霍夫矩阵是非常有特点的(删掉最后一行最后一列),首先看对角线,前n行为m,后m-1行为n。右上角和左下角各是一个$ n imes (m-1)$的$-1$块。手动消元一番,发现答案是$n^{m-1}m^{n-1}$,但是消到下半部分只能靠找规律,没有严谨的证明。交上去虽然A了,但是总觉得这个做法不是很靠谱,于是又学了一种非常科学的方法:
抛弃原始的按行消元,而是利用特殊的性质。将除第 $n$ 行以外的行加进第 $n$ 行里,此时第 $n$ 行变成这个样子:

此时第 $n+1$ 行往下是长这个样子的:
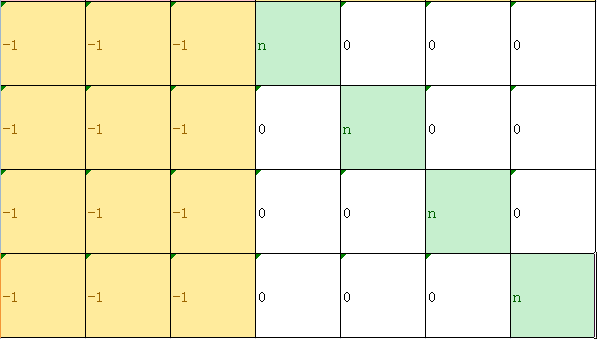
把之前消出来的那一行分别加到这些行里面,就只剩下绿色部分了,就像这样:

问题是这个奇怪的矩阵的行列式怎么求啊?看一看最早的定义式:
${det(K)=}sum_{P}^{ };{(}{(-1)}^{ au{(P)}} imes{K}_{1,p1} imes{K}_{2,p2} imes{K}_{3,p3} imescdots imes{K}_{N,pN}{)}$
显然每行每列只能选一个数出来,对于前 $n-1$ 列,如果选了 $n$ 行的1,第 $n$ 列就没得选了,所以如果想求有意义的答案,第 $n$ 行必然要选第 $n$ 个数,剩下每行的证明同理,所以这个矩阵的行列式求法等同于上三角矩阵,答案就是 $n^{m-1}m^{n-1}$ 有了准确的证明后感觉非常快乐.

1 # include <cstdio> 2 # include <iostream> 3 # define ll long long 4 5 using namespace std; 6 7 ll n,m,p,ans=1; 8 9 ll mul (ll a,ll b) 10 { 11 ll s=0; 12 while(b) 13 { 14 if(b&1LL) s=(a+s)%p; 15 a=(a+a)%p; 16 b>>=1LL; 17 } 18 return s%p; 19 } 20 21 ll qui (ll a,ll b) 22 { 23 ll s=1; 24 while(b) 25 { 26 if(b&1LL) s=mul(a,s); 27 a=mul(a,a); 28 b>>=1LL; 29 } 30 return s%p; 31 } 32 33 int main() 34 { 35 scanf("%lld%lld%lld",&n,&m,&p); 36 ans=mul(ans,qui(m,n-1)); 37 ans=mul(ans,qui(n,m-1)); 38 printf("%lld",ans); 39 return 0; 40 }
小Z的房间:https://www.lydsy.com/JudgeOnline/problem.php?id=4031
题意概述:求模 $10^9$ 意义下的生成树个数。$n<=90$
就是一道矩阵树模板题啦,只是模数不是质数有一点难办。回想矩阵树定理,有这样的性质:
“将两行进行交换,答案取反”;“将一行的k倍加到另一行里,答案不变”
所以就有了一种新的算法:数列欧几里得!
其实就是只关注每行要消去的那个数,将两行辗转相除,总复杂度是 $O(N^3loga_i)$.

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # define R register int 5 # define ll long long 6 7 using namespace std; 8 9 const int mod=1000000000; 10 const int maxn=90; 11 int n,m,id[maxn][maxn],cnt; 12 ll K[maxn][maxn]; 13 char s[maxn]; 14 15 int ab (int x) { if(x<0) return -x; return x; } 16 17 int Gauss () 18 { 19 ll t,ans=1; 20 for (R i=1;i<=n;++i) 21 for (R j=1;j<=n;++j) 22 K[i][j]=(K[i][j]%mod+mod)%mod; 23 for (R i=1;i<=n;++i) 24 { 25 for (R j=i+1;j<=n;++j) 26 { 27 while(K[j][i]) 28 { 29 t=K[i][i]/K[j][i]; 30 for (R k=i;k<=n;++k) 31 K[i][k]=(K[i][k]-K[j][k]*t%mod)%mod; 32 swap(K[i],K[j]); 33 ans*=-1; 34 } 35 } 36 ans=1LL*K[i][i]*ans%mod;; 37 } 38 return (ans%mod+mod)%mod; 39 } 40 41 int main() 42 { 43 scanf("%d%d",&n,&m); 44 for (R i=1;i<=n;++i) 45 { 46 scanf("%s",s+1); 47 for (R j=1;j<=m;++j) 48 { 49 if(s[j]=='*') continue; 50 id[i][j]=++cnt; 51 if(id[i-1][j]) 52 { 53 K[ id[i-1][j] ][ id[i-1][j] ]++; 54 K[ id[i][j] ][ id[i][j] ]++; 55 K[ id[i-1][j] ][ id[i][j] ]--; 56 K[ id[i][j] ][ id[i-1][j] ]--; 57 } 58 if(id[i][j-1]) 59 { 60 K[ id[i][j-1] ][ id[i][j-1] ]++; 61 K[ id[i][j] ][ id[i][j] ]++; 62 K[ id[i][j-1] ][ id[i][j] ]--; 63 K[ id[i][j] ][ id[i][j-1] ]--; 64 } 65 } 66 } 67 n=cnt-1; 68 printf("%d",Gauss()); 69 return 0; 70 }
重建:https://www.lydsy.com/JudgeOnline/problem.php?id=3534
题意概述:给定一张图,每条边有 $p\%$ 的概率出现,求出现的边恰好构成一棵生成树的概率。
从另一个方向理解矩阵树定理,发现它求的是这么一个式子:
$sum_Tprod_{e in T} omega_e$
这就很有启发性了...将边权改为边的出现概率,那么一棵树生成的概率就是所有边出现的概率的乘积...吗?其实并不是,构成一个树不仅需要这些边出现,还得要求别的边都不出现才行,于是有了这样的式子:
$sum_Tprod_{e in T} omega_e prod_{e otin T} (1-omega_e)$
但是这样的式子能求吗?正面求是不行的,我们只能求“属于”的,所以需要想办法让式子里消掉“不属于”的部分。这怎么做呢?容斥呀。
$prod_(1-omega_e)sum_Tprod_{e in T} frac{omega_e}{1-omega_e}$
把式子进行这样的变形后,需要用矩阵树求的值就只与“属于”树的边有关了,到这里再套板子就行。如果一条边存在的概率是一,那么就将它稍微调小一点点,否则会出现除以 $0$ 的情况。这题算的是相对误差,所以有点卡精度,首先eps要设到$10^{-10}$,输出时也要输出10位小数才可以。

1 # include <cstdio> 2 # include <iostream> 3 # include <cmath> 4 # include <algorithm> 5 # define R register int 6 7 using namespace std; 8 9 const double eps=1e-10; 10 const int maxn=52; 11 int n; 12 double K[maxn][maxn],S=1; 13 14 double Gauss() 15 { 16 n--; 17 double ans=1,t; 18 int maxx; 19 for (R i=1;i<=n;++i) 20 { 21 maxx=i; 22 for (R j=i+1;j<=n;++j) if(fabs(K[j][i])>fabs(K[maxx][i])) maxx=j; 23 if(maxx!=i) ans*=-1,swap(K[i],K[maxx]); 24 for (R j=i+1;j<=n;++j) 25 { 26 t=K[j][i]/K[i][i]; 27 for (R k=i;k<=n;++k) 28 K[j][k]-=K[i][k]*t; 29 } 30 ans*=K[i][i]; 31 } 32 return fabs(ans*S); 33 } 34 35 int main() 36 { 37 scanf("%d",&n); 38 for (R i=1;i<=n;++i) 39 for (R j=1;j<=n;++j) 40 scanf("%lf",&K[i][j]); 41 for (R i=1;i<=n;++i) 42 for (R j=1;j<=n;++j) 43 { 44 if(i==j) continue; 45 if(K[i][j]==1) K[i][j]-=eps; 46 if(i<j) S*=(1-K[i][j]); 47 K[i][i]+=K[i][j]/(1-K[i][j]); 48 K[i][j]=K[i][j]/(K[i][j]-1); 49 } 50 printf("%.10lf",Gauss()); 51 return 0; 52 }
社交网络:https://www.lydsy.com/JudgeOnline/problem.php?id=5297
题意概述:求一张有向图上的外向生成树个数(给定根),n<=250;
CQOI好奇怪...尤其是18年的题都不是很难,考察的点是卡常?
这是一道比较有趣的矩阵树,朴素的矩阵树可以解决无向图的生成树问题,有向图其实也差别不大。首先邻接矩阵是不变的-> $a[i][j]$ 表示 $i$ 到 $j$ 的连边情况;
外向树:边由根指向叶子,度数矩阵存入度; 内向树:边由叶子指向根,度数矩阵存出度;
求矩阵树首先需要删掉一行一列,如果指定了根,就必须删掉根所在的行列了。

1 # include <cstdio> 2 # include <iostream> 3 # define R register int 4 5 using namespace std; 6 7 const int maxn=260; 8 const int mod=10007; 9 int n,m,x,y,a[maxn][maxn]; 10 11 int qui (int a,int b) 12 { 13 int s=1; 14 while(b) 15 { 16 if(b&1) s=s*a%mod; 17 a=a*a%mod; 18 b>>=1; 19 } 20 return s; 21 } 22 23 int Gauss () 24 { 25 int ans=1,maxx; 26 for (R i=2;i<=n;++i) 27 { 28 maxx=i; 29 for (R j=i;j<=n;++j) if(a[j][i]>a[maxx][i]) maxx=j; 30 if(maxx!=i) swap(a[i],a[maxx]),ans=mod-ans; 31 for (R j=i+1;j<=n;++j) 32 { 33 if(!a[j][i]) continue; 34 int t=a[j][i]*qui(a[i][i],mod-2)%mod; 35 for (R k=i;k<=n;++k) 36 a[j][k]=(a[j][k]-a[i][k]*t%mod+mod)%mod; 37 } 38 ans=ans*a[i][i]%mod; 39 if(ans<0) ans+=mod; 40 } 41 return (ans%mod+mod)%mod; 42 } 43 44 int main() 45 { 46 scanf("%d%d",&n,&m); 47 for (R i=1;i<=m;++i) 48 { 49 scanf("%d%d",&x,&y); 50 a[y][x]--; a[x][x]++; 51 } 52 for (R i=2;i<=n;++i) 53 for (R j=2;j<=n;++j) 54 a[i][j]=(a[i][j]%mod+mod)%mod; 55 printf("%d",Gauss()); 56 return 0; 57 }
---shzr
