zoukankan html css js c++ java

树形dp

　　树上的dp虽然听起来挺可怕，其实却比较简单，因为dp要求最优子结构，有时候可能很难构造模型，但是树上自带子结构就非常棒啦！

树上背包：

　　树上的背包问题出现还挺多的，一般都与泛化物品有关系。树形依赖背包的最优做法是O(N^V),找了一篇国家队论文就是讲这个的，等有空的时候学一学。https://wenku.baidu.com/view/8ab3daef5ef7ba0d4a733b25.html

一般的题目似乎O(N*V^2)也没被卡过，在父节点处采取泛化物品合并的方法把儿子们都合起来就可以啦。

　　选课：https://www.luogu.org/problemnew/show/P2014

　　题目概述：在一棵树上选出x个点，若选到i点，则i点到根路径上的所有点也必选，使得点权和最大。

　　非常模板的树上背包，有一个问题在于所有的课不一定全部连通，这种问题已经成套路了，就是加一个虚点把所有的根都连上。这种加虚点的题一定要注意对于虚点的处理，对于这道题，m在读入后就要++，虚点的点权是0就可以啦。

关于加0计划，这道题的n完全可以再加一个0，O(N*V^2)的做法就跑不了了，得用正规的树上背包。

# include <cstdio>
# include <iostream>
# include <cstring>
# include <string>

# define R register int

using namespace std;

struct edge
{
    int to,nex;
};

int si,h=0,n,m;
edge g[605];
char c;
int firs[500]={0};
int dp[301][301],a[305]={0};// 在i及其子树中选择j门课所能得到的最大得分 
bool vis[301]={false};

void add(int u,int v)
{
    g[++h].to=v;
    g[h].nex=firs[u];
    firs[u]=h;
}

void dfs(int x)
{
    dp[x][1]=a[x];
    vis[x]=true;
    int j;
    for (R i=firs[x];i;i=g[i].nex)
    {
        j=g[i].to;
        if(j>n) continue;
        if(vis[j]) continue;
        dfs(j);
        for (R v=m+1;v>=2;v--)
          for (R k=1;k<=v;k++)
            dp[x][v]=max(dp[x][v],dp[x][k]+dp[j][v-k]);
    }
    return ;
}

int main()
{
    scanf("%d %d",&n,&m);
    memset(g,0,sizeof(g));
    for (R i=1;i<=n;i++)
    {
        scanf("%d%d",&si,&a[i]);
        add(i,si);
        add(si,i);
    }
    dfs(0);
    printf("%d",dp[0][m+1]);
    return 0;
}

选课

　　偷天换日: https://www.luogu.org/problemnew/show/P3360

　　题目概述：在一棵树上选出。。。其实和上一道差不多。

　　这道题的读入非常毒瘤，要递归读入，边权在转移的时候要乘二加进体积，且体积不能用光，对于每个叶子先做一个01背包，注意这些就没什么问题了。

# include <cstdio>
# include <iostream>

using namespace std;

struct edge
{
    int too,nex,co;
}g[6009];

int h=0,n,t,x,co,s=0;
int roo,firs[1009];
int dp[400][609];
int v[400],w[400];

void add(int x,int y,int co)
{
    g[++h].too=y;
    g[h].co=co;
    g[h].nex=firs[x];
    firs[x]=h;
}

void build(int roo)
{
    s++;
    int no=s;
    scanf("%d",&t);
    add(roo,no,t*2);
    scanf("%d",&x);
    if(x)
    {
        for (int i=1;i<=x;i++)
          scanf("%d%d",&v[i],&w[i]);
        for (int i=1;i<=x;i++)
          for (int j=n;j>=w[i];j--)
            dp[no][j]=max(dp[no][j],dp[no][j-w[i]]+v[i]);
    }
    else
    {
        build(no);
        build(no);
    }
    return ;
}

void dfs(int x)
{
    int j;
    for (int i=firs[x];i;i=g[i].nex)
    {
        j=g[i].too;    
        if(firs[j]) dfs(j);
        for (int vv=n;vv>=1;vv--)
          for (int z=0;z<=vv;z++)
          {
            if(vv-z-g[i].co>=0) dp[x][vv]=max(dp[x][vv],dp[x][z]+dp[j][vv-z-g[i].co]);
          }
    }
    return ;
}

int main()
{
    scanf("%d",&n);
    n--;
    build(0);
    dfs(0);
    printf("%d",dp[0][n]);
    return 0;
}

偷天换日

　　“访问”美术馆：https://www.luogu.org/problemnew/show/P1270

　　上一道题的弱化版，这两道题似乎不能用O(NV)的做法，因为每个结点都不是独立的物体，大概是这样。

# include <cstdio>
# include <iostream>

using namespace std;

struct edge
{
    int too,nex,co;
}g[6009];

int h=0,n,t,x,co,s=0;
int roo,firs[1009];
int dp[400][609];
int v[400],w[400];

void add(int x,int y,int co)
{
    g[++h].too=y;
    g[h].co=co;
    g[h].nex=firs[x];
    firs[x]=h;
}

void build(int roo)
{
    s++;
    int no=s;
    scanf("%d",&t);
    add(roo,no,t*2);
    scanf("%d",&x);
    if(x)
    {
        for (int i=1;i<=x;i++)
            dp[no][i*5]=i;
    }
    else
    {
        build(no);
        build(no);
    }
    return ;
}

void dfs(int x)
{
    int j;
    for (int i=firs[x];i;i=g[i].nex)
    {
        j=g[i].too;    
        if(firs[j]) dfs(j);
        for (int vv=n;vv>=1;vv--)
          for (int z=0;z<=vv;z++)
            if(vv-z-g[i].co>=0) dp[x][vv]=max(dp[x][vv],dp[x][z]+dp[j][vv-z-g[i].co]);
    }
    return ;
}

int main()
{
    scanf("%d",&n);
    n--;
    build(0);
    dfs(0);
    printf("%d",dp[0][n]);
    return 0;
}

“访问”美术馆

　　有线电视网：https://www.luogu.org/problemnew/show/P1273

　　题目概述：给定一棵有边权和点权的树，选出若干与根联通的路径，求收益不为负时选出的叶子结点个数的最大值。

　　树上背包。。。dp[i][j]表示以i为根的子树中收益为j的最大结点数。不得不说洛谷数据是真的弱，很多题解都是错的，其实对于某一棵子树可能会出现收益为负，但是只要整体收益不负也不是不可以，很多题解竟然数组先清0，还要取max，那不就相当于钦定每个点的收益都不为负了？如果不用正规做法的话此题就成了卡常神题，不能以n为体积来更新，要先统计一下每个点有几个儿子，加上这个玄学优化竟然水过了。

# include <cstdio>
# include <iostream>
# include <cstring>

using namespace std;

struct edge
{
    int co,nex,too;
}g[6009];

int a,c,k,rx,rf,n,m,h=0,ans;
int firs[3009],v[3009],son[3009];
char rc;
int dp[3009][3009];

void add(int x,int y,int co)
{
    g[++h].too=y;
    g[h].co=co;
    g[h].nex=firs[x];
    firs[x]=h;
}

inline int read()
{
    rx=0,rf=1;
    rc=getchar();
    while (!isdigit(rc))
    { 
        if (rc=='-') rf=-rf; 
        rc=getchar(); 
    }
    while (isdigit(rc))
    {
        rx=(rx<<3)+(rx<<1)+(rc^48); 
        rc=getchar(); 
    }
    return rx*rf;
}

void dfs(int x)
{
    int j;
    if(firs[x]==0) 
    {
        dp[x][1]=v[x];
        return ;
    }
    for (int i=firs[x];i;i=g[i].nex)
    {
        j=g[i].too;
        dfs(j);
        for (int s=son[x];s>=1;s--)
              for (int r=0;r<s;r++)
            {
              if(r&&dp[x][r]!=-2147483647&&dp[j][s-r]!=-2147483647) dp[x][s]=max(dp[x][s],dp[x][r]+dp[j][s-r]-g[i].co);
              if(r==0&&dp[j][s]!=-2147483647) dp[x][s]=max(dp[x][s],dp[j][s]-g[i].co);
            }
    }
    return ;
}

int build(int x)
{
    if(firs[x]==0)
        return 1;
    int ans=0,j;
    for (int i=firs[x];i;i=g[i].nex)
    {
        j=g[i].too;
        son[j]=build(j);
        ans+=son[j];
    }
    return ans;
}

int main()
{
    n=read();
    m=read();
    for (int i=1;i<=n;i++)
      for (int j=0;j<=m;j++)
        dp[i][j]=-2147483647;
    for (int i=1;i<=n-m;i++)
    {
        k=read();
        for (int j=1;j<=k;j++)
        {
            a=read();
            c=read();
            add(i,a,c);
        }
     }
     son[1]=build(1);
     for (int i=n-m+1;i<=n;i++)
         v[i]=read();
     dfs(1);
     for (int i=1;i<=m;i++)
         if(dp[1][i]>=0) ans=max(ans,i);
     printf("%d",ans);
     return 0;
}

有线电视网

　　[HAOI2010]软件安装：https://www.luogu.org/problemnew/show/P2515

　　题意概述：一些有依赖的软件，每个软件最多依赖另外的一个软件，有价值和体积，求最大价值。

　　看起来像是个普普通通的树形背包，然而依赖关系可以成环，我以为环是不能用的，然而wzx告诉我这道题强行要考缩点，所以缩完点可以一起安装...趁着软件还没反应过来一次把一个环上的都安上？缩完点还是普普通通的树形dp.

  1 // luogu-judger-enable-o2
  2 # include <cstdio>
  3 # include <iostream>
  4 # define R register int
  5 
  6 using namespace std;
  7 
  8 int n,m,Top,x,bp,cnt;
  9 int firs1[105],firs2[105],sta[105],w[105],v[105],color[105],V[105],W[105];
 10 int h1,h2,d[105],low[105],id[105],A[105],vis[105],r[105],dp[105][505];
 11 
 12 struct edge
 13 {
 14     int too,nex;
 15 }g1[1005],g2[1005];
 16 
 17 void add1(int x,int y)
 18 {
 19     g1[++h1].too=y;
 20     g1[h1].nex=firs1[x];
 21     firs1[x]=h1;
 22 }
 23 
 24 void add2(int x,int y)
 25 {
 26     g2[++h2].too=y;
 27     g2[h2].nex=firs2[x];
 28     firs2[x]=h2;
 29 }
 30 
 31 void dfs1(int x)
 32 {
 33     id[x]=low[x]=++cnt;
 34     sta[++Top]=x;
 35     vis[x]=true;
 36     int j;
 37     for (R i=firs1[x];i;i=g1[i].nex)
 38     {
 39         j=g1[i].too;
 40         if(!id[j]) 
 41         {
 42             dfs1(j),low[x]=min(low[x],low[j]);
 43         }
 44         else 
 45         {
 46             if(vis[j]) low[x]=min(low[x],low[j]);
 47         }
 48     }
 49     if(low[x]==id[x])
 50     {
 51         color[x]=++bp;
 52         vis[x]=false;
 53         V[bp]+=v[x];
 54         W[bp]+=w[x];
 55         while (sta[Top]!=x)
 56         {
 57             color[ sta[Top] ]=bp;
 58             V[bp]+=v[ sta[Top] ];
 59             W[bp]+=w[ sta[Top] ];
 60             vis[ sta[Top] ]=false;
 61             Top--;
 62         }
 63         Top--;
 64     }
 65 }
 66 
 67 void dfs2(int x)
 68 {
 69     for (R i=W[x];i<=m;++i) dp[x][i]=V[x];
 70     int j;
 71     for (R i=firs2[x];i;i=g2[i].nex)
 72     {
 73         j=g2[i].too;
 74         dfs2(j);
 75         for (R v=m-W[x];v>=0;v--)
 76             for (R k=0;k<=v;++k)
 77                 dp[x][v+W[x]]=max(dp[x][v+W[x]],dp[x][v+W[x]-k]+dp[j][k]);
 78     }
 79     return ;
 80 }
 81 
 82 int main()
 83 {
 84     scanf("%d%d",&n,&m);
 85     for (R i=1;i<=n;++i)
 86         scanf("%d",&w[i]);
 87     for (R i=1;i<=n;++i)
 88         scanf("%d",&v[i]);
 89     for (R i=1;i<=n;++i)
 90     {
 91         scanf("%d",&d[i]);
 92         if(d[i]==0) continue;
 93         add1(d[i],i);
 94     }
 95     for (R i=1;i<=n;++i)
 96             if(!id[i]) dfs1(i);
 97     for (R i=1;i<=n;++i)
 98     {
 99         if(color[i]!=color[ d[i] ]&&d[i])
100             add2(color[ d[i] ],color[i]),r[ color[i] ]++;
101     }
102     for (R i=1;i<=bp;++i)
103         if(!r[i]) add2(0,i);
104     dfs2(0);
105     printf("%d",dp[0][m]);
106     return 0;
107 }

软件安装

Others:

　　没有上司的舞会：https://www.luogu.org/problemnew/show/P1352

　　题目概述：树上…最大独立集？

　　这是我做的第一道树上dp，当时还是用邻接矩阵存的树，时间慢到不可思议，后来wzx教了我用邻接表又重构了一次，直接降到0ms，%%%wzx。因为树上的子结构，于是可以考虑用儿子来转移父亲。如果上司要去，下属就不能去，如果上司不去，下属去不去都可以。这道题的复杂度大概是O(N)的，所以再加3~4个零是没有太大问题的，下次造几个数据试试。

# include <cstdio>
# include <iostream>

using namespace std;

struct edge
{
    int too,nex;
}g[6009];

int h=0,n,Headmaster,clerk,boss,rx,rf;
char rc;
int T[6009],F[6009],firs[6009];
bool R[6009];

inline int read()
{
    rx=0,rf=1;
    rc=getchar();
    while (!isdigit(rc))
    { 
        if (rc=='-') rf=-rf; 
        rc=getchar(); 
    }
    while (isdigit(rc))
    {
        rx=(rx<<3)+(rx<<1)+(rc^48); 
        rc=getchar(); 
    }
    return rx*rf;
}

void add(int x,int y)
{
    g[++h].too=y;
    g[h].nex=firs[x];
    firs[x]=h;
}

void dp(int x)
{
    int j;
    for (int i=firs[x];i;i=g[i].nex)
    {
        j=g[i].too;
        if(firs[j]) dp(j);
        T[x]+=max(0,F[j]);
        F[x]+=max(T[j],max(F[j],0));
    }
    return ;
}

int main()
{
    n=read();
    for (int i=1;i<=n;i++)
        T[i]=read();
    for (int i=1;i<n;i++)
    {
        clerk=read();
        boss=read();
        add(boss,clerk);
        R[clerk]=true;
    }
    for (int i=1;i<=n;i++)
      if (!R[i]) 
      {
        Headmaster=i;
         break;
      }
    dp(Headmaster);
    printf("%d",max(T[Headmaster],F[Headmaster]));    
    return 0;
}

没有上司的舞会

　　战略游戏：https://www.luogu.org/problemnew/show/P2016

　　当然不是SDOI2018的那个啦。

　　题意概述：给定一颗树，选出最少的点使得所有的边都至少有一个端点被选中。

树上dp，如果儿子没有被选，那儿子与父亲的那条连边必须由父亲覆盖，如果儿子被选中，父亲可以不选。

# include <cstdio>
# include <iostream>
# define R register int

using namespace std;

int no,rx,rf,h=0,n,k,x,firs[1509],dep[1509];
int dp[1509][2];
char rc;
bool vis[1509],leaf[1509]={0};

struct edge
{
    int too,nex;
}g[3009];

void add(int x,int y)
{
    g[++h].too=y;
    g[h].nex=firs[x];
    firs[x]=h;
}

inline int read()
{
    rx=0,rf=1;
    rc=getchar();
    while (!isdigit(rc))
    { 
        if (rc=='-') rf=-rf; 
        rc=getchar(); 
    }
    while (isdigit(rc))
    {
        rx=(rx<<3)+(rx<<1)+(rc^48); 
        rc=getchar(); 
    }
    return rx*rf;
}

void build(int x)
{
    int j;
    for (R i=firs[x];i;i=g[i].nex)
    {
        j=g[i].too;
        if(dep[j]) continue;
        dep[j]=dep[x]+1;        
        build(j); 
    }
    return ;
}

void dfs(int x)
{
    int j;
    dp[x][1]=1;
    for (R i=firs[x];i;i=g[i].nex)
    {
        j=g[i].too;
        if(dep[j]<=dep[x]) continue;
        dfs(j);
        dp[x][1]+=min(dp[j][1],dp[j][0]);
        dp[x][0]+=dp[j][1];
    }
    return ;
}

int main()
{
    n=read();
    for (R i=0;i<n;i++)
    {
        no=read();
        k=read();
        for (R j=1;j<=k;j++)
        {
            x=read();
            add(no,x);
            add(x,no);
        }
    }
    dep[0]=1;
    build(0);
    dfs(0);
    printf("%d",min(dp[0][0],dp[0][1]));
    return 0;
}

战略游戏

　　做这道题的时候不知道在想什么，交了三次才过，回顾一下迷之错误。

　　　　　 1.这个不算错误：如果把根节点的深度认为是1，build时就不用设置vis数组，只要dep==0即为没访问过。

2.一开始对于每个节点是否是叶子进行了分类讨论，后来发现不仅没必要，还更容易出错，其实是不是叶子并没有什么关系。

3.对于一个叶子，不选他且覆盖全部子树边的方案数。。。是0啊！不要赋一个极大值！谁说这种情况不存在啊！

　　[SDOI2006]保安站岗：https://www.luogu.org/problemnew/show/P2458

　　题意概述：在一棵树上选出一些点，每个点可以覆盖与它有边相连的其它点，每个点有一个选的代价，求用最小的代价覆盖所有的点。

　　看起来非常easy啊，好像和上面那道一模一样啊，然后就只得了20分。仔细想一想发现并不一样，上面那道是覆盖所有的边，这个是覆盖所有的点...

　　$dp[x][0]$表示不选本身，用儿子覆盖所有的点的最小代价,$dp[x][1]$表示选自己的最小代价,$dp[x][2]$表示不选自己，用父亲覆盖自己的最小代价。转移有一点麻烦，但是和那道消防局的设立很像，其实这种题是有一个贪心做法的。

 1 // luogu-judger-enable-o2
 2 # include <cstdio>
 3 # include <iostream>
 4 # define R register int
 5 
 6 const int maxn=2000;
 7 int h,n,id,m,x,firs[maxn];
 8 int co[maxn],dp[maxn][3],dep[maxn];
 9 
10 int min(int a,int b)
11 {
12     if(a<b) return a;
13     return b;
14 }
15 
16 struct edge
17 {
18     int too,nex;
19 }g[maxn<<1];
20 
21 inline int read()
22 {
23     int x=0;
24     char c=getchar();
25     while (!isdigit(c))
26         c=getchar();
27     while (isdigit(c))
28     {
29         x=(x<<3)+(x<<1)+(c^48);
30         c=getchar();
31     }
32     return x;
33 }
34 
35 void add(int x,int y)
36 {
37     g[++h].too=y;
38     g[h].nex=firs[x];
39     firs[x]=h;
40 }
41 
42 void dfs(int x)
43 {
44     dp[x][1]=co[x];
45     int j;
46     for (R i=firs[x];i;i=g[i].nex)
47     {
48         j=g[i].too;
49         if(dep[j]!=0&&dep[j]<=dep[x]) continue;
50         dep[j]=dep[x]+1;
51         dfs(j);
52         dp[x][1]+=min(dp[j][0],min(dp[j][1],dp[j][2]));
53         dp[x][2]+=min(dp[j][0],dp[j][1]);
54     }
55     dp[x][0]=1e9;
56     for (R i=firs[x];i;i=g[i].nex)
57     {
58         j=g[i].too;
59         if(dep[j]!=0&&dep[j]<=dep[x]) continue;
60         dp[x][0]=min(dp[x][0],dp[x][2]-min(dp[j][1],dp[j][0])+dp[j][1]);
61     }
62     return ;
63 }
64 
65 int main()
66 {
67     scanf("%d",&n);
68     for (R i=1;i<=n;++i)
69     {
70         id=read();
71         co[id]=read();
72         m=read();
73         while (m--)
74         {
75             x=read();
76             add(x,id);
77             add(id,x);
78         }
79     }
80     dep[1]=1;
81     dfs(1);
82     printf("%d",min(dp[1][1],dp[1][0]));
83     return 0;
84 }

保安站岗

　　佳佳的魔法药水：https://www.luogu.org/problemnew/show/P1875

　　题意概述：给出n种药品的价格，以及一些合成表（用a和b制造c），求得到0号的最小价格以及方案数。

　　这道题的题解都是最短路计数，但是我写了一个很奇怪的树形DP(搜索)。本来想的是如果a+b=c则a，b为c的子树，然而可能有多组ab可以造c，所以用结构体&链表存子树就可以了！一种药水的最小代价可能是直接买（方案数:1）,也可能是某个或多个子树中ab方案数的积（生成a有x种，生成b有y种，所以生成的方案为 X*Y ），也可能是上边两者的和。

# include <cstdio>
# include <iostream>
# define R register 

using namespace std;

struct rec
{
    int x,y;
    int nex;
};

int a[1005]={0};// a[i]:合成或直接买i的最小代价 
int f[1005]={0};// f[i]:用a[i]的代价制造或买i的方案数 
rec b[1000008]={0}; //存边的结构体数组 
int n,h=0,x1,y1,to,x,F;
char c;//快读 
int firstt[1005]={0};
bool vis[1005]={false}; //vis[i]:i点的最小代价是否已经求出 

int readd()
{
    x=0,F=1,c=getchar();
    while (!isdigit(c))
    {
        if(c=='-') F=-F;
        c=getchar();
    }
    while (isdigit(c))
    {
        x=(x<<3)+(x<<1)+(c^48);
        c=getchar();
    }
    return x*F;
}

void dp(int n)
{
    for(R int i=firstt[n];i;i=b[i].nex) //枚举n点的子树 
    {
        int x,y;
        x=b[i].x;
        y=b[i].y;
        vis[n]=true;  //这个地方还是很重要的，因为数据中含有环，但是用自己和别人造自己显然是不合算的，所以要先打标记，不先打标记只能得10分 
        if(!vis[x]) dp(x);
        if(!vis[y]) dp(y);
        if(a[x]+a[y]<a[n]) 
        {
            a[n]=a[x]+a[y];
            f[n]=f[x]*f[y]; 
        }
        else
        if(a[x]+a[y]==a[n])
          f[n]+=f[x]*f[y];      
    }
}

int main()
{
    n=readd();
    for (R int i=0;i<n;i++)
    {
      a[i]=readd();
      f[i]=1;
    }
    while (scanf("%d%d%d",&x1,&y1,&to)!=EOF)  //链表 
    {
        b[++h].x=x1;
        b[h].y=y1;
        b[h].nex=firstt[to];
        firstt[to]=h;
    }
    dp(0);
    printf("%d %d",a[0],f[0]);
}

佳佳的魔法药水

　　今天点开学姐之前弄的树形dp题目单，发现还有一道题没做...

　　骑士：https://www.luogu.org/problemnew/show/P2607

　　题意概述：选出一些点，使得没有任何一个点与它痛恨的点在一起，且一个点有且仅有一个痛恨的点。$n<=10^6$

　　基环树$dp$.注意基环树不等于仙人掌...严格来说基环树不是树,但是对它的处理方法往往是断掉某一条边后做树形$dp$

　　$n$个点$n$条边必然是基环树,也可能是基环树森林,这个关系不大,对于每棵树单独做就行.

　　首先$dfs$找出环,在环上随便找出一个点,把与它相连的环边断掉一条,以这条边的两个端点分别作为根进行$dp$,此时不能选相连的另一个点.两种方法取$max$.

 1 // luogu-judger-enable-o2
 2 # include <cstdio>
 3 # include <iostream>
 4 # include <cstring>
 5 # include <cmath>
 6 # include <algorithm>
 7 # include <string>
 8 # define R register int
 9 # define ll long long
10 
11 using namespace std;
12 
13 const int maxn=1000006;
14 int n,m,h=1,cu,x,a[maxn],firs[maxn],vis[maxn],roo1,roo2,roo;
15 ll dp[maxn][2],t,ans;
16 struct edge
17 {
18     int too,nex;
19 }g[maxn<<1];
20 
21 void add (int x,int y)
22 {
23     g[++h].nex=firs[x];
24     firs[x]=h;
25     g[h].too=y;
26 }
27 
28 bool dfs (int x,int fa)
29 {
30     vis[x]=true;
31     int j;
32     for (R i=firs[x];i;i=g[i].nex)
33     {
34         j=g[i].too;
35         if(j==fa) continue;
36         if(vis[j])
37         {
38             roo1=x;
39             roo2=j;
40             cu=(i|1)-1;
41             return true;
42         }
43         if(dfs(j,x)) return true;
44     }
45     return false;
46 }
47 
48 void Dp (int x,int noo,int f)
49 {
50     int j;
51     dp[x][0]=0;
52     dp[x][1]=a[x];
53     vis[x]=true;
54     for (R i=firs[x];i;i=g[i].nex)
55     {
56         j=g[i].too;
57         if(j==f||i==cu||(i^1)==cu) continue;
58         Dp(j,noo,x);
59         dp[x][1]+=dp[j][0];
60         dp[x][0]+=max(dp[j][1],dp[j][0]);
61     }
62 }
63 
64 int main()
65 {
66     scanf("%d",&n);
67     for (R i=1;i<=n;++i)
68     {
69         scanf("%d%d",&a[i],&x);
70         add(i,x),add(x,i);
71     }
72     for (R i=1;i<=n;++i)
73         if(!vis[i]) 
74         {
75             dfs(i,0);
76             roo=roo1;
77             Dp(roo1,roo2,-1);
78             t=dp[roo1][0];
79             roo=roo2;        
80             Dp(roo2,roo1,-1);
81             t=max(t,dp[roo2][0]);
82             ans+=t;
83         }
84     printf("%lld",ans);
85     return 0;
86 }

骑士

　　[HNOI 2003] 消防局的设立：https://www.luogu.org/problemnew/show/P2279

　　题意概述：给定一棵树，选出的点可以覆盖距离不超过2的点，求最少要选出几个点。

　　其实还有个相似的题叫做将军令，那道题似乎可以贪心，也可以写非常复杂的dp，这道题就是它的弱化版了，决定练一下树形dp。

　　其实这道题写dp非常复杂啊...理性分析一下：$dp[i][j]$表示第$i$个点第$j$种状态时所需的最少点数。听起来很棒！然后再看一下需要哪几种状态。

　　1.选自己；2；选了至少一个儿子；3.选了至少一个孙子；4.能覆盖所有儿孙，不一定覆盖自己(伟大的奉献精神...)；5.能覆盖所有的孙子。

　　考虑一下复杂的转移过程：

　　1.如果选了自己，那么儿子选与不选都可以，用所有儿子的5种状态中最小值的和加1即可；

　　2.如果选了至少一个儿子，就可以用这个儿子覆盖其他的所有儿子，但是除了那个选出的儿子的儿子，其他的儿子的儿子（孙子）就必须再找方法覆盖了，可以用其他点的1-4状态来转移。那么选择哪一个点呢？选出那个1状态与min(1,2,3,4)状态差别最大的。

　　3.选了某个孙子，也就是说某个儿子选择了2状态。其余的儿子必须用1-3状态进行转移。那么选择哪一个儿子呢？也是选出2状态与min(1,2,3)差别最小的。

　　4.一个比一个复杂，然而这个却出人意料的简单明了：如果只能覆盖到儿孙，其实也就是所有儿子的1-3状态取min求和；

　　5.所有儿子的1-4状态取min求和。

　　所以真是一道复杂的dp呢。

　　后来看了一个题解，学了一种比较简单的方法，用dp[i][k] (k>=2)表示min(dp[i][1],dp[i][2]...dp[i][k]),转移起来比较方便。

 1 # include <cstdio>
 2 # include <iostream>
 3 
 4 using namespace std;
 5 
 6 int dp[1001][5],n,firs[1001];
 7 int k,a[1001],h,mi;
 8 struct edge
 9 {
10     int too,nex;
11 }g[1005];
12 
13 void add(int x,int y)
14 {
15     g[++h].too=y;
16     g[h].nex=firs[x];
17     firs[x]=h;
18 }
19 
20 int main()
21 {
22     scanf("%d",&n);
23     for (int i=2;i<=n;++i)
24     {
25         scanf("%d",&a[i]);
26         add(a[i],i);
27     }
28     for (int i=n;i>=1;--i)
29     {
30         int m1=1e7,m2=1e7;
31         dp[i][0]=1;
32         for (int j=firs[i];j;j=g[j].nex)
33         {
34             k=g[j].too;
35             dp[i][0]+=dp[k][4];
36             dp[i][3]+=dp[k][2];
37             dp[i][4]+=dp[k][3];
38             m1=min(m1,dp[k][0]-dp[k][3]);
39             m2=min(m2,dp[k][1]-dp[k][2]);
40         }
41         dp[i][1]=dp[i][4]+m1;
42         dp[i][2]=dp[i][3]+m2;
43         dp[i][2]=min(dp[i][2],min(dp[i][0],dp[i][1]));
44         dp[i][3]=min(dp[i][3],dp[i][2]);
45         dp[i][4]=min(dp[i][4],dp[i][3]);
46     }
47     printf("%d",dp[1][2]);
48     return 0;
49 }

消防局的设立

　　会议：https://www.luogu.org/problemnew/show/P1395

　　题意概述：在树上找出一个点，使得其他所有点到它的距离最小。

　　指定根以后就是有根树了，首先dfs一次，求出每个点下方的点到它的距离，再进行第二次dfs，用父亲更新儿子，求出其他点到它的距离。方程比较复杂，想清楚再写。

 1 # include <cstdio>
 2 # include <iostream>
 3 
 4 using namespace std;
 5 
 6 const int maxn=50009;
 7 int n,h;
 8 int F[maxn],firs[maxn],dp1[maxn],an[maxn],p[maxn],ans;
 9 struct edge
10 {
11     int too,nex;
12 }g[maxn<<1];
13 
14 void add (int x,int y)
15 {
16     g[++h].too=y;
17     g[h].nex=firs[x];
18     firs[x]=h;
19 }
20 
21 void dfs1 (int x)
22 {
23     p[x]=1;
24     int j;
25     for (int i=firs[x];i;i=g[i].nex)
26     {
27         j=g[i].too;
28         if(j==F[x]) continue;
29         F[j]=x;
30         dfs1(j);
31         p[x]+=p[j];
32         dp1[x]+=dp1[j]+p[j];
33     }
34 }
35 
36 void dfs2 (int x)
37 {
38     int j;
39     for (int i=firs[x];i;i=g[i].nex)
40     {
41         j=g[i].too;
42         if(j==F[x]) continue;
43         an[j]=an[x]-dp1[j]-p[j]+n-p[j]+dp1[j];
44         dfs2(j);
45     }
46 }
47 
48 int main()
49 {
50     scanf("%d",&n);
51     int a,b;
52     for (int i=1;i<n;++i)
53     {
54         scanf("%d%d",&a,&b);
55         add(a,b);
56         add(b,a);
57     }
58     dfs1(1);
59     an[1]=dp1[1];
60     dfs2(1);
61     ans=an[1];
62     for (int i=1;i<=n;++i)
63         ans=min(ans,an[i]);
64     for (int i=1;i<=n;++i)
65         if(ans==an[i])
66         {
67             printf("%d %d",i,ans);
68             return 0;
69         }
70 }

会议

　　伟大的奶牛聚集：https://www.luogu.org/problemnew/show/P2986

　　和上面那个题非常相似，只不过多了点权和边权，其实本质上还是一样的。

 1 # include <cstdio>
 2 # include <iostream>
 3 # define R register int
 4 
 5 using namespace std;
 6 
 7 const int maxn=100009;
 8 int n,a,b,l,h=0;
 9 int c[maxn],firs[maxn],dep[maxn],siz[maxn];
10 long long dp[maxn],Sum=0;
11 struct edge
12 {
13     int too,nex,co;
14 }g[maxn<<1];
15 
16 int read()
17 {
18     int x=0;
19     char c=getchar();
20     while (!isdigit(c))
21         c=getchar();
22     while (isdigit(c))
23     {
24         x=(x<<3)+(x<<1)+(c^48);
25         c=getchar();
26     }
27     return x;
28 }
29 
30 void add (int x,int y,int z)
31 {
32     g[++h].too=y;
33     g[h].nex=firs[x];
34     firs[x]=h;
35     g[h].co=z;
36 }
37 
38 void dfs1 (int x)
39 {
40     int j;
41     siz[x]=c[x];
42     for (R i=firs[x];i;i=g[i].nex)
43     {
44         j=g[i].too;
45         if(dep[j]) continue;
46         dep[j]=dep[x]+1;
47         dfs1(j);
48         siz[x]+=siz[j];
49         dp[x]+=dp[j]+(long long)siz[j]*g[i].co;
50     }
51 }
52 
53 void dfs2 (int x)
54 {
55     int j;
56     for (R i=firs[x];i;i=g[i].nex)
57     {
58         j=g[i].too;
59         if(dep[j]<=dep[x]) continue;
60         dp[j]+=dp[x]-dp[j]+(long long)(Sum-2*siz[j])*g[i].co;
61         dfs2(j);
62     }
63 }
64 
65 int main()
66 {
67     scanf("%d",&n);
68     for (R i=1;i<=n;++i)
69         c[i]=read(),Sum+=c[i];
70     for (R i=1;i<n;++i)
71     {
72         a=read(),b=read(),l=read();
73         add(a,b,l);
74         add(b,a,l);
75     }
76     dep[1]=1;
77     dfs1(1);
78     dfs2(1);
79     long long ans=dp[1];
80     for (R i=1;i<=n;++i)
81         ans=min(ans,dp[i]);
82     printf("%lld",ans);
83     return 0;
84 }

伟大的奶牛聚集

　　最大子树和：https://www.luogu.org/problemnew/show/P1122

　　题意概述:在一棵树上切掉一些枝条,使得剩下的点权和最大.

　　非常简单的题目.$dp_i$表示以$i$为根的子树内选择$i$的最大收益,转移时如果发现某个子树的最大收益是负数就切掉好了.注意$1$号点不一定选，所以答案要边做边取.这道题写的比较早,可能出现码风不符的情况..

 1 # include <cstdio>
 2 # include <iostream>
 3 
 4 using namespace std;
 5 
 6 const int N=32005;
 7 
 8 int n,x,y,szr=0,top=0,ans=0;
 9 int a[N]={0};
10 int dp[N]={0};
11 int E[N]={0},son[N]={0},next[N]={0};
12 
13 
14 void add(int x,int y)
15 {
16     next[++top]=son[x];
17     son[x]=top;
18     E[top]=y;
19 }
20 
21 int dfs(int x,int f)
22 {
23     int S=a[x];
24     for (register int i=son[x];i;i=next[i])
25       if(E[i]!=f)
26         S+=max(dfs(E[i],x),0);
27     ans=max(ans,S);
28     return S;
29 }
30 
31 int main()
32 {
33     scanf("%d",&n);
34     for (register int i=1;i<=n;i++)
35         scanf("%d",&a[i]);
36     for (register int i=1;i<n;i++)
37     {
38       scanf("%d%d",&x,&y);
39       add(x,y);
40       add(y,x);
41     }
42     ans=a[1];
43     dfs(1,0);
44     printf("%d",ans);
45     return 0;
46 }

最大子树和

　　附近的牛：https://www.luogu.org/problemnew/show/P3047　

　　题意概述：给定一棵带点权的树，求距离每个点距离不超过$k$的点的点权和.

　　经典的$up$ $and$ $down$的题目,首先肯定是要二维状态啦,$dp[i][j]$表示$i$的子树内与$i$的距离不超过$k$的点权和,一遍$dfs$就可以求解了,现在考虑$down$,从父亲直接更新显然是不行的,还要减掉本来就是从它更新过去的那些答案.用父亲更新儿子时注意循环的顺序,否则就会出现循环更新了.记得$asuldb$五月份的时候就切了这个题,他真的好神啊,我估计他不可能来翻这么早的文章了,而且他还没有$cnblog$的账号，所以$\%\%\%\%\%\%\%\%\%\%\%\%\%\%\%$

 1 # include <cstdio>
 2 # include <iostream>
 3 # define R register int
 4 
 5 using namespace std;
 6 
 7 const int maxn=100009;
 8 int x,y,n,k,h;
 9 int dp[maxn][21],firs[maxn],dep[maxn];
10 struct edge
11 {
12     int too,nex;
13 }g[maxn<<1];
14 
15 inline int read()
16 {
17     int x=0;
18     char c=getchar();
19     while (!isdigit(c)) c=getchar();
20     while (isdigit(c))  x=(x<<3)+(x<<1)+(c^48),c=getchar();
21     return x;
22 }
23 
24 inline void add (int x,int y)
25 {
26     g[++h].too=y;
27     g[h].nex=firs[x];
28     firs[x]=h;
29 }
30 
31 void dfs1 (int x)
32 {
33     int j;
34     for (R i=firs[x];i;i=g[i].nex)
35     {
36         j=g[i].too;
37         if(dep[j]) continue;
38         dep[j]=dep[x]+1;
39         dfs1(j);
40         for (R z=1;z<=k;++z)
41             dp[x][z]+=dp[j][z-1];
42     }
43 }
44 
45 void dfs2 (int x,int roo)
46 {
47     int j;
48     if(roo!=0)
49         for (R z=k;z>=2;--z)
50                dp[x][z]+=dp[roo][z-1]-dp[x][z-2];
51     dp[x][1]+=dp[roo][0];
52     for (R i=firs[x];i;i=g[i].nex)
53     {
54         j=g[i].too;
55         if(j==roo) continue;
56         dfs2(j,x);
57     }
58 }
59 
60 int main()
61 {
62     n=read(),k=read();
63     for (R i=1;i<n;++i)
64         x=read(),y=read(),add(x,y),add(y,x);
65     for (R i=1;i<=n;++i)
66         dp[i][0]=read();
67     dep[1]=1;
68     dfs1(1);
69     dfs2(1,0);
70     int s;
71     for (R i=1;i<=n;++i)
72     {
73         s=0;
74         for (R j=0;j<=k;++j)
75             s+=dp[i][j];
76         printf("%d
",s);
77     }
78     return 0;
79 }

附近的牛

　　HOT-Hotel:https://www.luogu.org/problemnew/show/P3565

　　题意概述:给定一棵没有边权的树(相当于边权都是$1$),求有多少三元组$(x,y,z)$满足两两之间的距离相等.$n<=5000$

　　考虑三个点怎么才能满足这个条件,显然两两距离都是$1$是不可能的(树上出现三角形的环),那么距离至少是$2$,而且距离是奇数似乎都不行...那么只要是偶数距离就必然有一个中间点，三个点到它的距离是一样的.首先一遍$n^2$的树形$dp$求出距离每个点距离为$k$的点的个数,枚举中心点统计即可(思考一下).

　　真的吗?这样很显然是不行的啊...从样例就能看出来这个做法的错误了,举个栗子.

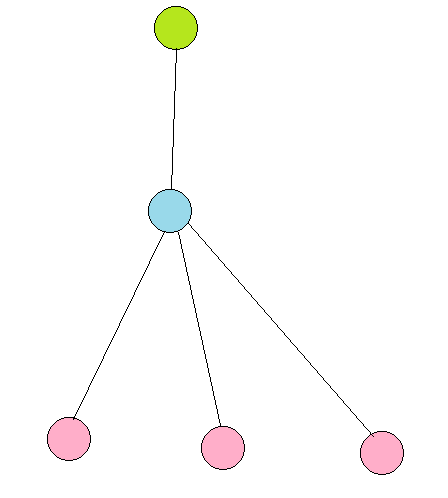
　　那三个粉色的点会在蓝色和绿色处分别被统计一次...

　　观察发现如果每个点只统计以他为根时,三个点分居不同子树的答案就不会重复了,组合数瞎搞一下就好了.然后我就被卡内存了,然后我就开了$short$,然后我就过了.

  1 # include <cstdio>
  2 # include <iostream>
  3 # include <queue>
  4 # include <cstring>
  5 # include <string>
  6 # define R register int
  7 # define ll long long
  8 
  9 using namespace std;
 10 
 11 const int maxn=5003;
 12 int x,y,n,h,firs[maxn],dep[maxn],len[maxn];
 13 short f[maxn][maxn],d[maxn][maxn];
 14 long long c[maxn][4],ans;
 15 struct edge
 16 {
 17     int too,nex;
 18 }g[maxn<<1];
 19 
 20 void add (int x,int y)
 21 {
 22     g[++h].too=y;
 23     g[h].nex=firs[x];
 24     firs[x]=h;
 25 }
 26 
 27 void Up (int x)
 28 {
 29     int j;
 30     f[x][0]=1;
 31     for (R i=firs[x];i;i=g[i].nex)
 32     {
 33         j=g[i].too;
 34         if(dep[j]) continue;
 35         dep[j]=dep[x]+1;
 36         Up(j);
 37         len[x]=max(len[x],len[j]+1);
 38     }
 39     for (R i=firs[x];i;i=g[i].nex)
 40     {
 41         j=g[i].too;
 42         if(dep[j]<dep[x]) continue;
 43         for (R k=0;k<=len[j];++k)
 44             f[x][k+1]+=f[j][k];
 45     }
 46 }
 47 
 48 void Down (int x)
 49 {
 50     int j;
 51     for (R i=firs[x];i;i=g[i].nex)
 52     {
 53         j=g[i].too;
 54         if(dep[j]<dep[x]) continue;
 55         for (R k=n;k>=2;--k)    
 56             d[j][k]=f[x][k-1]+d[x][k-1]-f[j][k-2];
 57         d[j][1]++;
 58         Down(j);
 59     }    
 60 }
 61 
 62 void dp (int x)
 63 {
 64     int k=0;
 65     for (R i=1;i<=n;++i)
 66     {
 67         ans+=c[ f[x][i]+d[x][i] ][3];
 68         for (R j=firs[x];j;j=g[j].nex)
 69         {
 70             k=g[j].too;
 71             if(dep[k]<dep[x]) continue;
 72             ans-=c[ f[k][i-1] ][3];
 73             ans-=c[ f[k][i-1] ][2]*(f[x][i]+d[x][i]-f[k][i-1]);
 74         }
 75         ans-=c[ d[x][i] ][3];
 76         ans-=c[ d[x][i] ][2]*f[x][i];
 77     }
 78     for (R i=firs[x];i;i=g[i].nex)
 79     {
 80         k=g[i].too;
 81         if(dep[k]<dep[x]) continue;
 82         dp(k);
 83     }
 84 }
 85 
 86 int main()
 87 {
 88     scanf("%d",&n);
 89     for (R i=1;i<n;++i)
 90     {
 91         scanf("%d%d",&x,&y);
 92         add(x,y);
 93         add(y,x);
 94     }
 95     c[0][0]=1;
 96     for (R i=1;i<=n;++i)
 97     {
 98         c[i][0]=1;
 99         for (R j=1;j<=3;++j)
100             c[i][j]=c[i-1][j-1]+c[i-1][j];
101     }
102     dep[1]=1;
103     Up(1);
104     Down(1);
105     dp(1);
106     printf("%lld",ans);
107     return 0;
108 }

HOT-Hotel

　　树：https://lydsy.com/JudgeOnline/problem.php?id=2466

　　题意概述：给定一棵树，每个点上有灯，初始时都为关闭，选择一些点，将

---shzr

查看全文

相关阅读:
delete误删除恢复
 oracle自增字段
 oracle唯一约束
 linux得到系统当前日期
 to_char+fm
oracle范围分区
 oracle之use_hash用法
 oracle11g的regexp函数
 第一个脚本输入参数
 使用ctl将txt或csv文件导入表数据

原文地址：https://www.cnblogs.com/shzr/p/9064722.html