贪心

贪心

　　正妹吃月饼：https://www.luogu.org/problemnew/show/P2431

　　题意概述：在$m-n$的区间中找出一个二进制表示中$1$最多的数，输出那个数有多少个$1$；

 

---

 

　　倒水：https://www.luogu.org/problemnew/show/P1582

　　题意概述：把$n$个装有一升水的瓶子经过合并变成不多于$k$个，可以买新的瓶子。(只有两个水量相同的瓶子才可以倒在一起）

　　这题真神奇啊，可以发现，合并到最后，每个瓶子里的水必然都是$2$的幂次方，所以我们求的就是 $sum_{i=1}^k2^{a_{i}}>=n$

　　求这个式子成立时总和减去 $n$ 的最小值。这样看起来好像不是很好做，但是每个大数都可以分解成两个小数，显然并不划算，所以只要不超过$n$，用越大的数越好。一旦已经用了$k-1$个，最后一个就必须大于$n$的剩余值。这道题有一个小细节，注意不要对$0$取$log$。这样就做完了。

　　

# include <cstdio>
# include <cmath>

using namespace std;

long long n;
int k;
long long p[35];

int main()
{
    scanf("%lld%d",&n,&k);
    p[0]=1;
    for (int i=1;i<=33;++i)
        p[i]=p[i-1]<<1;
    while (k>1)
    {
        if(n!=0)
            n-=p[ (int)floor( log2(n) ) ];
        k--;
    }
    if(n!=0) printf("%lld",p[ (int)ceil( log2(n) ) ]-n);
    else printf("0");
    return 0;
}

 

---

 

　　末日的传说：https://www.luogu.org/problemnew/show/P1338

　　题意概述：求一个最小的$1-n$的全排列,使得其中有m个逆序对，保证有解。

　　首先这里有一个暴力做法：$next-permutation$加树状数组。

　　这道题在洛谷的数学问题试炼场里，然而是个贪心。一个数列最多有$n*(n-1)/2$个逆序对，此时整个数列是降序的。现在回到这道题目，首先把$1$放进数列里面，放在开头：之后最多只能产生(n-1)*(n-2)/2个逆序对，如果这个数大于$m$，就可以把$1$放在结尾，因为这样生成的排列最小。如果放在结尾就会产生$n-1$个逆序对。按照这种贪心的思路一直安排好每一个数，就是答案了，非常巧妙。

　　

# include <cstdio>
# include <iostream>
# include <algorithm>

using namespace std;

int n,m;
int h,t;
int a[50005];

int main()
{
    scanf("%d%d",&n,&m);
    h=1,t=n;
    for (int i=1;i<=n;++i)
    {
        if((long long)(n-i)*(n-i-1)/2>=m)
            a[h++]=i;
        else
            a[t--]=i,m-=(t-h+1);
    }
    for (int i=1;i<=n;++i)
        printf("%d ",a[i]);
    return 0;
}

---

　　

　　国王游戏：https://www.luogu.org/problemnew/show/P1080

　　题意概述:$n$个人排成一排，每个人的得分等于他前面所有人的左手数的乘积整除他自己右手数的商，最小化最大得分。

　　这道题以前听人讲过，思路很有代表性。假设已经排好了n个人，如果交换相邻的两个人使得答案不能更优，需要满足什么条件呢？假设之前所有人左手数的乘积为s，前一个人的左手数为a，右手为b，后一个人的左手数为c，右手数为d。

　　不交换的最大得分为

　

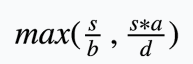
　　交换的最大得分为

　　

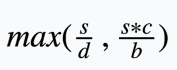
　　进行一下替换：$ans_1=max(r_1,r_2)$，$ans_2=max(r_3,r_4),r_2>r_3,r_4>r_1,ans_1<ans_2$,所以可以发现$r_4>r_2$,按照这个方法排排序就行啦。然后这道题要加高精度...

　　

# include <cstdio>
# include <iostream>
# include <algorithm>

using namespace std;

int A,B;
int n,t[10000],ans[10000],SS[10000],S[10000];
struct peo
{
    int l,r;
}a[1009];

bool cmp(peo a,peo b)
{
    return a.l*a.r<b.l*b.r;
}

void writ()
{
    while (ans[ ans[0] ]==0&&ans[0]) ans[0]--;
    for (int i=ans[0];i>=1;--i)
    {
        printf("%d",ans[i]);
    }
    if(ans[0]==0) printf("0");
}

void mul(int x)
{
    for (int i=1;i<=S[0];++i)
        S[i]*=a[x].l;
    for (int i=1;i<=S[0]+5;++i)
    {
        S[i+1]+=S[i]/10;
        S[i]%=10;
    }
    S[0]+=5;
    while (S[S[0]]==0&&S[0]) S[0]--;
}

void div(int x)
{
    for (int i=0;i<=S[0];++i)
        SS[i]=S[i];
    for (int i=SS[0];i>=1;--i)
    {
        SS[i]+=(SS[i+1]%x)*10;
        SS[i+1]/=x;
    }
    SS[1]/=x;
    while (SS[SS[0]]==0&&SS[0]) SS[0]--;
    while (ans[ans[0]]==0&&ans[0]) ans[0]--;
    if(SS[0]<ans[0]) return ;
    if(ans[0]<SS[0])
    {
        for (int i=0;i<=SS[0];++i)
            ans[i]=SS[i];
        return ;
    }
    for (int i=ans[0];i>=1;--i)
    {
        if(ans[i]>SS[i]) return;
        if(ans[i]<SS[i])
        {
            for (int i=0;i<=SS[0];++i)
            ans[i]=SS[i];
            return ;
        }
    }
    return ;
}

int main()
{
    scanf("%d",&n);
    scanf("%d%d",&A,&B);
    S[1]=A;
    for (int i=1;i<=5;i++)
        S[i+1]+=S[i]/10,S[i]%=10;
    while (S[S[0]]==0&&S[0]) S[0]--;
    S[0]=5;
    for (int i=1;i<=n;++i)
        scanf("%d%d",&a[i].l,&a[i].r);
    sort(a+1,a+1+n,cmp);
    for (int i=1;i<=n;++i)
    {
        div(a[i].r);
        mul(i);
    }
    writ();
    return 0;
}

---

　　观光公交：https://www.luogu.org/problemnew/show/P1315

　　题意概述：一辆公交车开在路上，有人说要从几号车站坐到几号车站以及几点到达开始车站，有一些氮气加速器，求怎么加速使得所有人的旅行时间最少。

---

　　

　　种树：https://www.luogu.org/problemnew/show/P1484

　　题意概述：在长度为n的序列中选出不超过k个不相邻的点，使得点权和最大。

　　有一个dp的方法，$dp[i][j]=max(dp[i-1][j],dp[i-2][j-1]+a[i])$,但是会TLE。

　　假设k等于1，那必然是选点权最大的点或者不选；

　　如果k大于1，那可以再选一个离之前选过的点比较远的点，或者删掉某个点之后选它两边的点。

　　所以就是贪心啦,链表写起来非常好玩啊。

　　

# include <cstdio>
# include <iostream>
# include <cmath>
# include <queue> 
# define R register int

using namespace std;

int N,rf,n,k,l[1000009],r[1000009];
long long rx,a[1000005];
typedef pair <long long,int> pii;
priority_queue <pii,vector<pii>,less<pii> > q;
char rc;
bool vis[1000009];
pii t;

long long read()
{
    rx=0,rf=1;
    rc=getchar();
    while (!isdigit(rc))
    {
        if(rc=='-') rf=-rf;
        rc=getchar();
    }
    while (isdigit(rc))
    {
        rx=(rx<<3)+(rx<<1)+(rc^48);
        rc=getchar();
    }
    return rx*rf;
}

int main()
{
    scanf("%d%d",&n,&k);
    N=n;
    for (R i=1;i<=n;++i)
    {
        a[i]=read();
        q.push(make_pair(a[i],i));
        l[i]=i-1;
        r[i]=i+1;
    }
    long long ans=0;
    while (k--)
    {
        t=q.top();
        q.pop();
        while (q.size()&&vis[t.second])
        {
            t=q.top();
            q.pop();    
        }
        int id=t.second;
        int v=t.first;
        if(v<0) break;
        ans+=v;
        vis[id]=true;
        vis[l[id]]=true;
        vis[r[id]]=true;
        N++;
        l[N]=l[ l[id] ];
        r[ l[N] ]=N;
        r[N]=r[ r[id] ];
        l[ r[N] ]=N;
        a[N]=a[ l[id] ]+a[ r[id] ]-a[id];
        q.push(make_pair(a[N],N));
    }
    printf("%lld",ans);
    return 0;
}

---

　　旅行家的预算：https://www.luogu.org/problemnew/show/P1016

　　题意概述：旅行家从城市$1$到$n$,路上经过的每个点都可以加油，每个点的油价不同，油箱有最大容量，求用最少的钱加油到达终点所需的最少钱数。

　　非常贪心...从头开始，如果从目前的起点加满油可以到达一个油价更低的地方，就加正好够去那个点的油，如果之后都没有更便宜的，就先加满油，再开到能开到的地方中最便宜的地方。如果从某一个点即使加满油也到不了下一个点，就输出无解。

　　

# include <cstdio>
# include <iostream>

using namespace std;

double res,m,d1,c,d2,p;
int n;
double co,D[10],P[10];

int main()
{
    scanf("%lf%lf%lf%lf%d",&d1,&c,&d2,&p,&n);
    for (int i=1;i<=n;++i)
        scanf("%lf%lf",&D[i],&P[i]);
    P[0]=p;
    D[n+1]=d1;
    int i=0;
    while (i<=n)
    {
        double m1=P[i],m2=P[i+1];
        int x1,x2=i+1;
        for (int j=i;j<=n+1;++j)
        {
            if((res+c)*d2<D[j]-D[i]) break;
            if(P[j]<m1&&m1==P[i]) m1=P[j],x1=j;
            if(P[j]<m2&&j!=i) m2=P[j],x2=j;
        }
        if((res+c)*d2<D[i+1]-D[i]) break;
        if(m1!=P[i])
        {
            co+=((D[x1]-D[i])/d2-res)*P[i];
            i=x1;
            res=0;
        }
        else
        {
            co+=(c-res)*P[i];
            res=c-(D[x2]-D[i])/d2;
            i=x2;
        }
    }
    if(i!=n+1) 
        printf("No Solution");
    else
        printf("%.2lf",co);
    return 0;
}

---

　　

　　皇后游戏：https://www.luogu.org/problemnew/show/P2123

　　题意概述：和国王游戏挺像的，不知道为什么公式总是插入失败，看图吧。

　　

　  果然还是插入图片比较好用呢...

　　看到这么相似的题面就猜到要贪心（从洛谷贪心区找出来的),所以就仿照那一道题证了一下，然后发现很不可做啊！

　　首先我发现这个东西并不是很好化简啊...于是我决定按照某本书讲的方法，从较小的情况看起。

　　

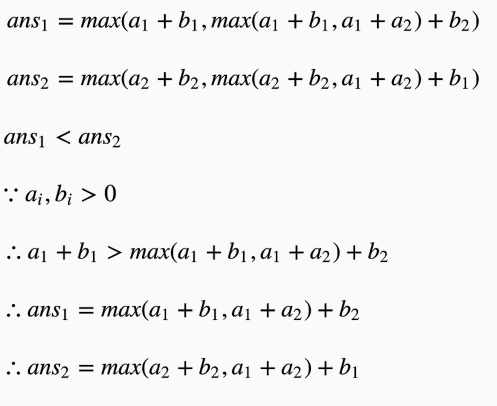
　　这个结果至少在n<=2的时候的确是对的，但是扩展开来就不能保证正确性了，然而它过了比较大的那个样例，于是我开心地把它交了上去：30；

　　于是现在来看一看正确的证明过程吧：

　　

　　

　　这道题的思路很巧妙，证明非常麻烦。写这个题用时十分钟，证明过程&&整理笔记用了3个小时...

　　我的排序思路被Hack了，因为不具有传递性，除非用冒泡才行...从题解区学了一种具有传递性的cmp函数，重构了一下。　　　　

　　感谢liuzibujian dalao的题解。

　　

# include <cstdio>
# include <iostream>
# include <algorithm>

using namespace std;

int T,n;
long long no,su,las;
long long ans=0;
struct peo
{
    int a,b,d;
}a[20005];

bool cmp(peo a,peo b)
{
    if(a.d!=b.d) return a.d<b.d;
    if(a.d<=0) return a.a<b.a;
    return a.b>b.b;
}

int SS (int x)
{
    if(x<0) return -x;
    return x;
}

int main()
{
    scanf("%d",&T);
    while (T--)
    {
        ans=0;
        su=0;
        las=0;
        scanf("%d",&n);
        for (int i=1;i<=n;++i)
        {
            scanf("%d%d",&a[i].a,&a[i].b);
            a[i].d=0;
            if(a[i].a!=a[i].b) a[i].d=(a[i].a-a[i].b)/(SS(a[i].a-a[i].b));
        }
        sort(a+1,a+1+n,cmp);
        for (int i=1;i<=n;++i)
        {
            if(i==1) 
                no=a[i].a+a[i].b;
            else
                no=max(las,su+a[i].a)+a[i].b;
            ans=max(ans,no);
            las=no;
            su+=a[i].a;
        }
        printf("%lld
",ans);
    }
    return 0;
}

---

　　智力大冲浪：https://www.luogu.org/problemnew/show/P1230

　　题意概述：给定n个任务，每个任务需要一单位时间完成，如果在给定时间内完成才有收益，每个任务的收益不同，找出一个最优的顺序使得收益最大化。

　　贪心，按照收益排序，从截止时间往前找，只要有空就塞进去，如果都没有就放到最后。为什么正确？如果一个任务在安排时发现截止时间前都安排满了，那就必须从前面找出一个来替换，但是之前的任务收益必然比它大，所以不能换。LOJ上还有一个加强版，理论上卡$N^2$做法，但是只要加一个前指针表示从1到指针处都满了也能过...似乎并没有理论正解。

　　

# include <cstdio>
# include <iostream>
# include <algorithm>

using namespace std;

int n,m;
bool vis[505],f;
struct nod
{
    int w,t;
}a[505];

bool cmp (nod a,nod b)
{
    return a.w>b.w;
}

int main()
{
    scanf("%d%d",&m,&n);
    for (int i=1;i<=n;++i)
        scanf("%d",&a[i].t);
    for (int i=1;i<=n;++i)
        scanf("%d",&a[i].w);
    sort(a+1,a+1+n,cmp);
    for (int i=1;i<=n;++i)
    {
        f=false;
        for (int j=a[i].t;j>=1;--j)
            if(!vis[j])
            {
                vis[j]=true;
                f=true;
                break;
            }
        if(f) continue;
        for (int j=n;j>=1;--j)
            if(!vis[j])
            {
                vis[j]=true;
                m-=a[i].w;
                break;
            }
    }
    printf("%d",m);
    return 0;
}

 

---

  

　　糖果传递：https://www.luogu.org/problemnew/show/P2512

　　题意概述：有$n$个小朋友坐成一圈，每人有$a_i$个糖果。每人只能给左右两人传递糖果。每人每次传递一个糖果代价为$1$。

 

---

 

　　阿狸与桃子的游戏:https://lydsy.com/JudgeOnline/problem.php?id=2563

　　题意概述:给定一张无向图,点有点权,两个人轮流选点,选完后,如果某条边的两端都被同一个人选了,那么他可以额外得到这条边的分数,要求最大化两个人的得分差.

　　看起来有点像网络流,不知道行不行,但是这里说一种特别简洁的做法:

　　首先发现这道题要求的不是最大得分,而是得分差,这里看起来好像很有趣.发现如果某条边的两端被不同的人选了,就都不得分,那么是不是也可以认为每人得一半的分呢?这样如果一个人把两个点都选走了,它就可以得到整个分数了.如果两个人分别选,相减之后还是等于都没有得分.把每条边的边权都分到点上,排个序,两个人按照顺序轮流选就可以得到答案.(luogu上大家齐心合力的把它评成了黑题)

　　

# include <cstdio>
# include <iostream>
# include <algorithm>
# define ll long long
# define R register int

using namespace std;

const int maxn=10004;
int n,m,x,y,z;
double v[maxn],a,b;

int main()
{
    scanf("%d%d",&n,&m);
    for (R i=1;i<=n;++i)
        scanf("%lf",&v[i]);
    for (R i=1;i<=m;++i)
    {
        scanf("%d%d%d",&x,&y,&z);
        v[x]+=(double)z/2;
        v[y]+=(double)z/2;
    }
    sort(v+1,v+1+n);
    for (R i=n;i>=1;--i)
        if(i%2) b+=v[i];
        else a+=v[i];
    printf("%.0lf",a-b);
    return 0;
}

---

 

　　钓鱼：https://loj.ac/problem/10009

　　题意概述：一条直线上有$n$个鱼塘,每个鱼塘里有鱼,每个鱼塘第一次钓时可以钓到$f_i$条鱼,等到下一次鱼的数量就会减少$d_i$,当然不会成负数,一开始站在$1$号鱼塘,相邻的鱼塘间有一个距离,求给定时间内最多钓多少鱼.$n<=100$

　　其实是挺水的一个题,但是第一次见的时候觉得太难了就一直没做,直到今天一看:

　　

　　不过还是要做一下,消除一下心理阴影.

　　首先这道题最重要的就是走的距离,只要确定了走的距离,用于钓鱼的时间也就确定了,所以...枚举最远走到哪个鱼塘即可.把每个鱼塘能钓到的鱼扔进一个堆里,每次取出最大值加进答案并更新这个鱼塘的鱼数即可.

　　

# include <cstdio>
# include <iostream>
# include <cstring>
# include <queue>
# define R register int

using namespace std;

int n,h;
int f[105],d[105],t[105],ans;
struct a
{
    int id,val;
    bool operator > (const a &b) const{
        return val>b.val;
    }
    bool operator < (const a &b) const{
        return val<b.val;
    }
};
priority_queue <a> q;

int solve (int n,int t)
{
    int ans=0;
    a x;
    while (q.size()) q.pop();
    for (R i=1;i<=n;++i)
    {
        x.id=i;
        x.val=f[i];
        q.push(x);
    }
    for (R i=1;i<=t;++i)
    {
        x=q.top();
        q.pop();
        ans+=x.val;
        x.val=max(0,x.val-d[x.id]);
        q.push(x);
    }
    return ans;
}

int main()
{
    scanf("%d%d",&n,&h);
    h*=12;
    for (R i=1;i<=n;++i)
        scanf("%d",&f[i]);
    for (R i=1;i<=n;++i)
        scanf("%d",&d[i]);
    for (R i=2;i<=n;++i)
        scanf("%d",&t[i]),t[i]+=t[i-1];
    for (R i=1;i<=n;++i)
        if(h>t[i]) ans=max(ans,solve(i,h-t[i]));
        else break;
    printf("%d",ans);
    return 0;
}

---shzr