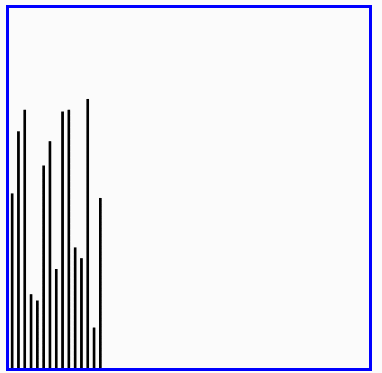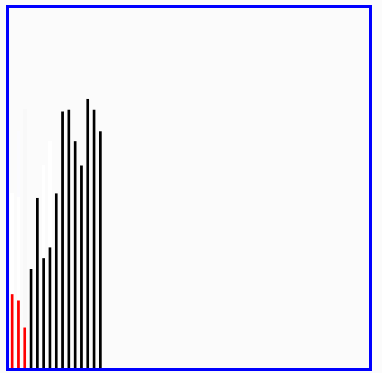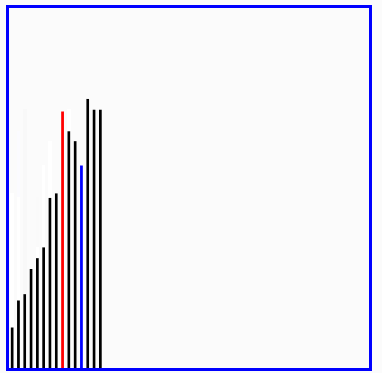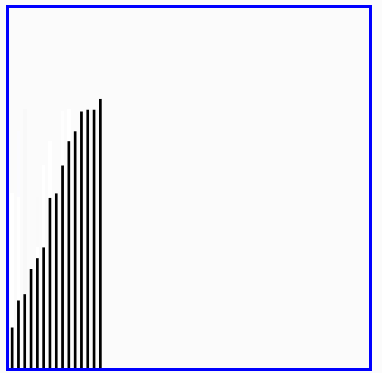
(1)快速排序:
快速排序(英语:Quicksort),又称划分交换排序(partition-exchange sort),通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
步骤为:
1.从数列中挑出一个元素,称为"基准"(pivot),
2.重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区结束之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
3.递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
递归的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递归下去,但是这个算法总会结束,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。
(2)快速排序的分析:
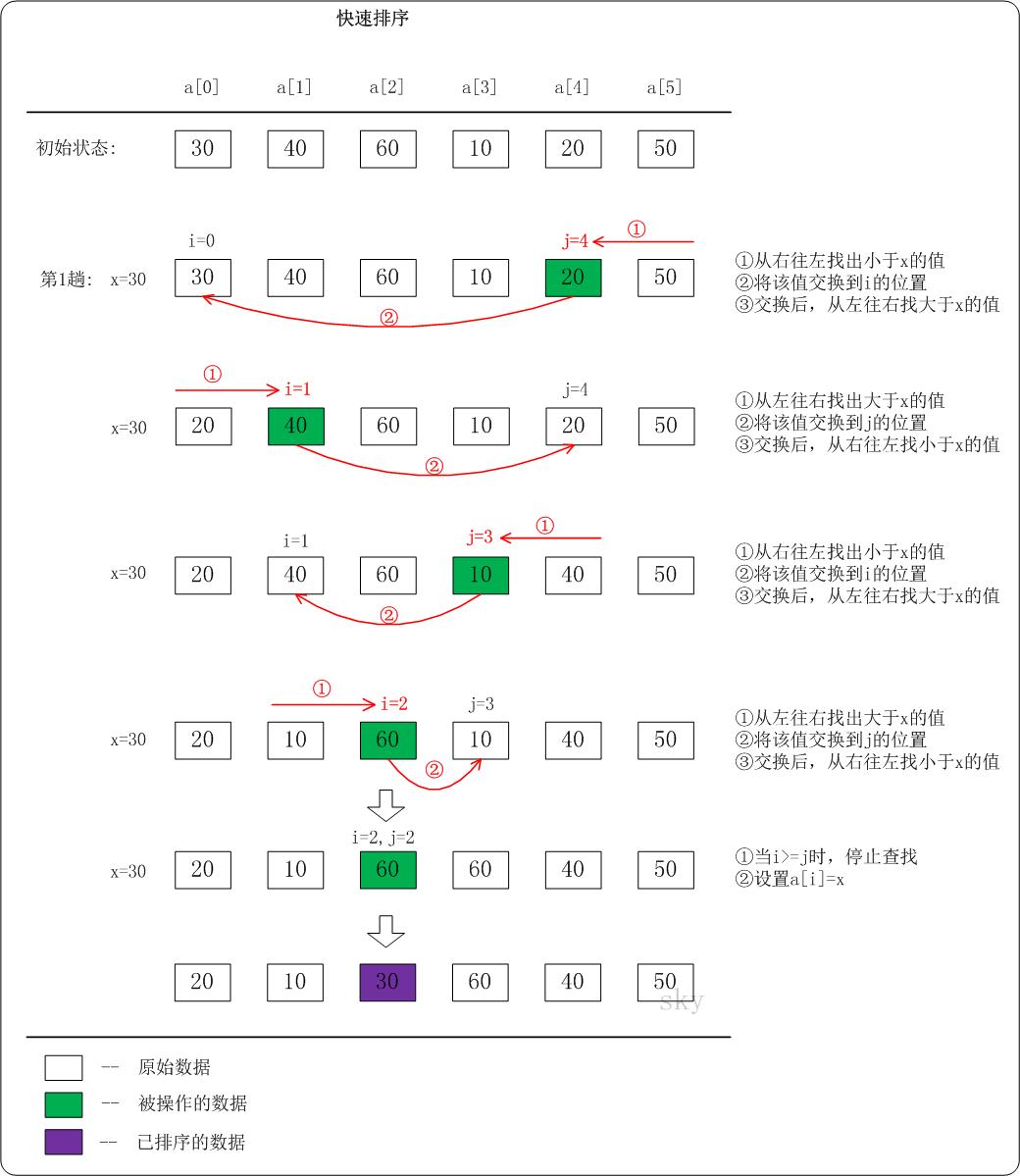
(3)代码实现:
1 def quick_sort(alist, first, last): 2 """快速排序""" 3 if first >= last: # 总体递归结束条件 4 return 5 mid = alist[first] 6 low = first 7 high = last 8 while low < high: 9 # high游标左移 10 while low < high and alist[high] >= mid: # 注意并列的两个while只有一个有=号,才能保证相同的元素在同一边 11 high -= 1 12 alist[low] = alist[high] 13 14 # low游标右移 15 while low < high and alist[low] < mid: 16 low += 1 17 alist[high] = alist[low] 18 # 从循环退出时,low==high 19 alist[low] = mid # <==>alist[high] = mid 20 21 # 对low左边的列表执行快速排序 22 quick_sort(alist, first, low-1) # quick_sort(alist[:low-1]) 23 24 # 对low右边的列表执行快速排序 25 quick_sort(alist, low+1, last) # quick_sort(alist[low+1:]) 26 27 28 if __name__ == "__main__": 29 li = [54, 26, 93, 17, 77, 31, 44, 55, 20] 30 print(li) 31 quick_sort(li, 0, len(li)-1) 32 print(li)
(4)运行结果:
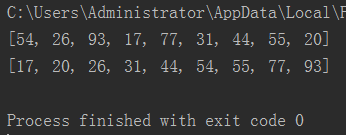
(5)时间复杂度:
最优时间复杂度:O(n log n)
最坏时间复杂度:O(n2)
稳定性:不稳定
从一开始快速排序平均需要花费O(n log n)时间的描述并不明显。但是不难观察到的是分区运算,数组的元素都会在每次循环中走访过一次,使用O(n)的时间。在使用结合(concatenation)的版本中,这项运算也是O(n)。
在最好的情况,每次我们运行一次分区,我们会把一个数列分为两个几近相等的片段。这个意思就是每次递归调用处理一半大小的数列。因此,在到达大小为一的数列前,我们只要作 log n 次嵌套的调用。这个意思就是调用树的深度是O(log n)。但是在同一层次结构的两个程序调用中,不会处理到原来数列的相同部分;因此,程序调用的每一层次结构总共全部仅需要O(n)的时间(每个调用有某些共同的额外耗费,但是因为在每一层次结构仅仅只有O(n)个调用,这些被归纳在O(n)系数中)。结果是这个算法仅需使用O(n log n)时间。
(6)快速排序演示: