二叉树基本操作

该二叉树可以实现二叉树的几种遍历操作，包括先序，中序，后序以及层序遍历，以及输出树的深度，添加节点等等。tree.c存放了二叉树的基本操作函数，treemain.c为主函数文件用来验证二叉树的各种操作的，代码如下：
tree.c文件

//start from the very beginning,and to create greatness
//@author: Chuangwei Lin
//@E-mail：979951191@qq.com
//@brief： 二叉树的基本操作
#include "tree.h"
/******************************************************
函数名：BinTreeInit(ChainBinTree *node)
参数：树节点
功能：初始化二叉树根结点 
*******************************************************/
ChainBinTree *BinTreeInit(ChainBinTree *node) 
{
     if(node!=NULL) //若二叉树根结点不为空 
         return node;
     else
         return NULL;
}
/******************************************************
函数名：BinTreeAddNode(ChainBinTree *bt,ChainBinTree *node,int n)
参数：bt为父结点，node为子结点,n=1表示添加左子树，n=2表示添加右子树 
功能：添加数据到二叉树 
*******************************************************/
int BinTreeAddNode(ChainBinTree *bt,ChainBinTree *node,int n)
{//该函数没有实现分配空间，将在另一个函数分配
    if(bt==NULL)
    {
        printf("父结点不存在，请先设置父结点!
");
        return 0;
    } 
    switch(n)
    {
        case 1: //添加到左结点 
            if(bt->left) //左子树不为空 
            {
                printf("左子树结点不为空!
");
                return 0;
            }else
                bt->left=node;
            break;
        case 2://添加到右结点
            if( bt->right) //右子树不为空 
            {
                printf("右子树结点不为空!
"); 
                return 0;
            }else
                bt->right=node;
            break;
        default:
            printf("参数错误!
");
            return 0;
    }
    return 1;
}
/******************************************************
函数名：BinTreeLeft(ChainBinTree *bt)  
参数：父节点
功能：返回左子结点
*******************************************************/
ChainBinTree *BinTreeLeft(ChainBinTree *bt)   
{
    if(bt)
        return bt->left;
    else
        return NULL;
}
/******************************************************
函数名：BinTreeRight(ChainBinTree *bt) 
参数：父节点
功能：返回右子结点
*******************************************************/
ChainBinTree *BinTreeRight(ChainBinTree *bt) 
{
    if(bt)
        return bt->right;
    else
        return NULL;
}
/******************************************************
函数名：BinTreeIsEmpty(ChainBinTree *bt)  
参数：二叉树节点
功能：检查二叉树是否为空，为空则返回1,否则返回0 
*******************************************************/
int BinTreeIsEmpty(ChainBinTree *bt)  
{
    if(bt)
        return 0;
    else
        return 1;
} 
/******************************************************
函数名：BinTreeDepth(ChainBinTree *bt)  
参数：二叉树节点
功能：求二叉树深度
*******************************************************/
int BinTreeDepth(ChainBinTree *bt)  
{
    int dep1,dep2;
    if(bt==NULL)
        return 0; //对于空树，深度为0
    else
    {
        dep1 = BinTreeDepth(bt->left); //左子树深度 (递归调用)
        dep2 = BinTreeDepth(bt->right); //右子树深度 (递归调用)
        if(dep1>dep2)
           return dep1 + 1; 
        else
            return dep2 + 1; 
    } 
} 
/******************************************************
函数名：BinTreeFind(ChainBinTree *bt,DATA data)
参数：树节点，欲查找的元素值
功能：在二叉树中查找值为data的结点
*******************************************************/
ChainBinTree *BinTreeFind(ChainBinTree *bt,DATA data) 
{
    ChainBinTree *p;
    if(bt==NULL)//若为空则返回
        return NULL;
    else
    {
        if(bt->data==data)
            return bt; 
        else{ // 分别向左右子树递归查找 
            if(p=BinTreeFind(bt->left,data))
                return p;
            else if(p=BinTreeFind(bt->right, data)) 
                return p;
            else
                return NULL; 
        } 
    } 
} 
/******************************************************
函数名：BinTreeClear(ChainBinTree *bt)
参数：数节点
功能：清空二叉树，使之变为一棵空树
*******************************************************/
void BinTreeClear(ChainBinTree *bt) 
{
     if(bt)//若该节点不空则清空其左右子树
     {
         BinTreeClear(bt->left); //清空左子树 
         BinTreeClear(bt->right);//清空右子树 
         free(bt);//释放当前结点所占内存 
         bt=NULL;
     }
     return; 
}
/******************************************************
函数名：BinTree_DLR(ChainBinTree *bt,void (*oper)(ChainBinTree *p))
参数：树节点，处理函数指针
功能：先序遍历
*******************************************************/
void BinTree_DLR(ChainBinTree *bt,void (*oper)(ChainBinTree *p))  
{     
     if(bt)//树不为空，则执行如下操作 
     {
         oper(bt); //处理结点的数据 
         BinTree_DLR(bt->left,oper);
         BinTree_DLR(bt->right,oper);
     }
     return; 
} 
/******************************************************
函数名：BinTree_LDR(ChainBinTree *bt,void(*oper)(ChainBinTree *p))
参数：树节点，处理函数指针
功能：中序遍历 
*******************************************************/
void BinTree_LDR(ChainBinTree *bt,void(*oper)(ChainBinTree *p))   
{
     if(bt)//树不为空，则执行如下操作 
     {
         BinTree_LDR(bt->left,oper); //中序遍历左子树
         oper(bt);//处理结点数据 
         BinTree_LDR(bt->right,oper); //中序遍历右子树/
     }
     return; 
} 
/******************************************************
函数名：BinTree_LRD(ChainBinTree *bt,void(*oper)(ChainBinTree *p))
参数：树节点，处理函数指针
功能： 后序遍历
*******************************************************/
void BinTree_LRD(ChainBinTree *bt,void (*oper)(ChainBinTree *p)) 
{
     if(bt)
     {
         BinTree_LRD(bt->left,oper); //后序遍历左子树 
         BinTree_LRD(bt->right,oper); //后序遍历右子树/
         oper(bt); //处理结点数据
     }
     return; 
}
/******************************************************
函数名：oper(ChainBinTree *p) 
参数：树节点
功能：操作二叉树结点数据
*******************************************************/
void oper(ChainBinTree *p)  
{
     printf("%c ",p->data); //输出数据
     return;
}
/******************************************************
函数名：BinTree_Level(ChainBinTree *bt,void (*oper)(ChainBinTree *p)) 
参数：树节点，处理函数指针
功能： 按层遍历
*******************************************************/
void BinTree_Level(ChainBinTree *bt,void (*oper)(ChainBinTree *p))  
{
     ChainBinTree *p;
     ChainBinTree *q[QUEUE_MAXSIZE]; //定义一个顺序队列 
     int head=0,tail=0;//队首、队尾序号 
     if(bt)//若队首指针不为空     
     {//tail队尾指针是指向队尾的下一个位置的
         tail=(tail+1)%QUEUE_MAXSIZE;//计算循环队列队尾序号 
         q[tail] = bt;//将二叉树根指针进队
     }
     while(head!=tail) //队列不为空，进行循环 ，进队列还有操作数据
     {//取余实现队列的循环，边进边取出来处理，处理之后其左右子树才进队列
         head=(head+1)%QUEUE_MAXSIZE; //计算循环队列的队首序号，所以while前面要先进队一次 
         p=q[head]; //获取队首元素 
         oper(p);//处理队首元素 
         if(p->left!=NULL) //若结点存在左子树，则左子树指针进队 
         {
             tail=(tail+1)%QUEUE_MAXSIZE;//计算循环队列的队尾序号 
             q[tail]=p->left;//将左子树指针进队 
         }              
         if(p->right!=NULL)//若结点存在右孩子，则右孩子结点指针进队 
         {
             tail=(tail+1)%QUEUE_MAXSIZE;//计算循环队列的队尾序号 
             q[tail]=p->right;//将右子树指针进队 
         }
     }
     return; 
}
/******************************************************
函数名：InitRoot()
参数：无
功能：初始化二叉树的根
*******************************************************/
ChainBinTree *InitRoot()   
{
    ChainBinTree *node;
    if(node=(ChainBinTree *)malloc(sizeof(ChainBinTree))) //分配内存
    {
        printf("
输入根结点数据:");
        scanf("%s",&node->data);
        node->left=NULL;
        node->right=NULL;
        return BinTreeInit(node);
    }
    return NULL;
}
/******************************************************
函数名：AddNode(ChainBinTree *bt)
参数：数节点
功能：向二叉树指定的节点添加子节点
*******************************************************/
void AddNode(ChainBinTree *bt)
{
     ChainBinTree *node,*parent;
     DATA data;
     char select;
    if(node=(ChainBinTree *)malloc(sizeof(ChainBinTree))) //分配内存
    {
        printf("
输入二叉树结点数据:");
        scanf("%s",&node->data);
        node->left=NULL; //设置左右子树为空 
        node->right=NULL;
        printf("输入父结点数据:");//新增的节点是在指定父节点下面
        scanf("%s",&data);
        parent=BinTreeFind(bt,data);//查找指定数据的结点 
        if(!parent)//若未找到指定数据的结点 
        {
            printf("未找到父结点!
");
            free(node); //释放创建的结点内存 
            return;
         }
         printf("1.添加到左子树
2.添加到右子树
");
         do{
            select=getchar();
            select-='0';
            if(select==1 || select==2)
                BinTreeAddNode(parent,node,select); //添加结点到二叉树 
         }while(select!=1 && select!=2);
    }
    return ;
}

treemain.c文件

//start from the very beginning,and to create greatness
//@author: Chuangwei Lin
//@E-mail：979951191@qq.com
//@brief： 二叉数结构的测试程序
#include "tree.h"
int main(int argc, char const *argv[])
{
    ChainBinTree *root=NULL; //root为指向二叉树根结点的指针 
    char select;
    void (*oper1)(); //指向函数的指针 
    oper1=oper; //指向具体操作的函数 
    do{
        printf("1.设置二叉树根元素    2.添加二叉树结点
");
        printf("3.先序遍历二叉树      4.中序遍历二叉树
");
        printf("5.后序遍历二叉树      6.层序遍历二叉树
");
        printf("7.输出二叉树深度      0.退出
");
        select=getchar();
        switch(select){
        case '1': //设置根元素 
             root=InitRoot();
             break;
        case '2': //添加结点 
             AddNode(root);//这里输入根节点即可，到时是查找父节点的值在添加节点的
             break;
        case '3'://先序遍历二叉树 
             printf("先序遍历结果如下；
");
             BinTree_DLR(root,oper1);
             printf("
");
             break;
        case '4'://中序遍历二叉树 
             printf("中序遍历结果如下：
");
             BinTree_LDR(root,oper1);
             printf("
");
             break;
        case '5'://后序遍历
             printf("后序遍历结果如下：
");
             BinTree_LRD(root,oper1);
             printf("
");
             break;
        case '6'://层序遍历
             printf("层序遍历结果如下：
");
             BinTree_Level(root,oper1);
             printf("
");
             break;
        case '7'://输出二叉树的深度
             printf("
二叉树的深度为：%d
",BinTreeDepth(root));
        case '0':
             break;
        }
        select=getchar();//这里加一个去掉回车符
    }while(select!='0');
    BinTreeClear(root);//清空二叉树 
    root=NULL;
    return 0;
}

tree.h主要是基本结构体和各种函数的声明

//start from the very beginning,and to create greatness
//@author: Chuangwei Lin
//@E-mail：979951191@qq.com
//@brief： 二叉树基本操作头文件
#include <stdio.h> 
#include <stdlib.h> 
#define QUEUE_MAXSIZE 50
typedef char DATA;       //定义元素类型 
typedef struct ChainTree  //定义二叉树结点类型 
{
    DATA data;              //元素数据
    struct ChainTree *left; //左子树结点指针
    struct ChainTree *right;//右子树结点指针
}ChainBinTree;
//各函数声明
ChainBinTree *BinTreeInit(ChainBinTree *node);
int BinTreeAddNode(ChainBinTree *bt,ChainBinTree *node,int n);
ChainBinTree *BinTreeLeft(ChainBinTree *bt);
ChainBinTree *BinTreeRight(ChainBinTree *bt);
int BinTreeIsEmpty(ChainBinTree *bt);
int BinTreeDepth(ChainBinTree *bt);
ChainBinTree *BinTreeFind(ChainBinTree *bt,DATA data);
void BinTreeClear(ChainBinTree *bt);
void BinTree_DLR(ChainBinTree *bt,void (*oper)(ChainBinTree *p));
void BinTree_LDR(ChainBinTree *bt,void(*oper)(ChainBinTree *p));
void BinTree_LRD(ChainBinTree *bt,void (*oper)(ChainBinTree *p));
void oper(ChainBinTree *p);
void BinTree_Level(ChainBinTree *bt,void (*oper)(ChainBinTree *p));
ChainBinTree *InitRoot();
void AddNode(ChainBinTree *bt);

Makefile文件也比较简单

#目标是lcwtree，右边为依赖
lcwtree:*.o 
    gcc -o lcwtree *.c 

clean:
    rm -f *.o 

运行结果如下：
我通过增加结点建立了如下的二叉树：

                                          - a
                                  b                  c
                    d                     e                   f

其他过程如下：

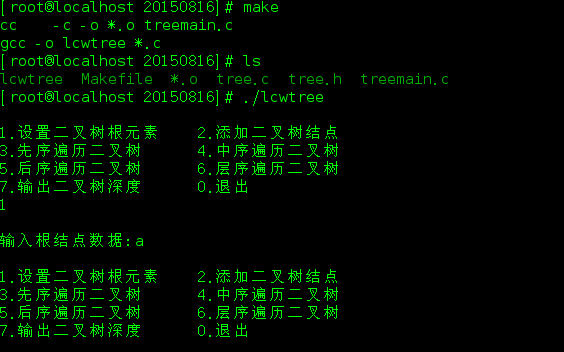
先序遍历：

中序遍历：

后序遍历：

层序遍历：