【斯坦福算法分析和设计】作业1(附视频)

 

附上一个视频，如何理解一个算法:

https://www.bilibili.com/video/BV1iZ4y1W7ep

• 选择题
• Q1
• Q2
• Q3
• Q4
• Q5
• 编码题

选择题

Q1

题目

3-way-MergeSort: 假设不将 MergeSort 的每一步分成两半，而是分成三份，单独进行排序，最后将它们全部合并。 该算法的整体渐近运行时间是多少？ （提示：请注意，合并步骤仍然可以在O(n)时间内实施。）

解答

Step 1: 写下循环

 # 当n是1的时候排序是O(1)

表示长度为n的数组的运行时间。而MergeSort将数组分成了三份，所以每份数组长度是，而合并步骤可以在O(n)时间完成，所以整个的运行时间如下:

Step 2: 假设 ，令，因此我们有

 # 在k=0时

 # 把k和n的关系带入step1的公式2

Step 3: 于是我们可以解决这个问题

 # 一直这样拆分

 # 去掉常数项

 # 把k根据上面的假设换成n

 

Q2

题目

给你函数f和g，使得。 那么吗?（这里c是正常数。）你应该假定f和g非递减，并且始终大于1。

解答

根据大O的定义，存在正常数和，时，有

让我们得出左侧的边界，我们有

为了进一步简化，我们得到，所以我们有

 带入公式

 # 提取公共项

 # 使用g(n)非递减性质

所以，存在正常数和，当时，有

于是

 

Q3

题目

再次假设两个（正）非递减函数f和g，使得。 那么吗？

解法

不完全是，让我们来检查一些简单的特殊情况。

情况1: f(n)=g(n)=n，这种情况下，2n=O(2n)是正确的。

情况2: f(n)=10n，g(n)=n，这种情况下我们有 # 课程2里面证明过，指数函数的指数和一个常数相乘改变了它的渐进性增长率。

这样，我们可以确定：

该说法并不总是正确的。

该说法并非总是错误的。

那么怎么让这种说法总是正确呢？

根据大O的定义，存在正常数c和，使得的时候，有，就是说，只需要让就好了。

 

Q4

题目

k-way-MergeSort： 假设给定k个排序数组，每个数组包含n个元素，并且你想将它们组合成一个kn个元素的单个数组。 考虑以下方法:

• 使用讲座中讲解的merge子程序，你可以合并前两个数组
• 然后将第三个给定数组与前两个数组的合并版本合并
• 然后将第四个给定数组与前三个数组的合并版本合并，依此类推
• 直到合并到最后一个（kth）输入数组为止。

将k，n作为输入，那么这个函数的运行时间是多少？

解法

为简单起见，我们说合并所需的时间仅等于列表长度的总和。(因为所有数组已经排好序了，只需要线性遍历它们)

因此对于第一次合并，我们有

对于第二次合并，我们有

...

这些数字的总和为

 

Q5

题目

）。

解法

一个比较简单的方法是计算一堆值：

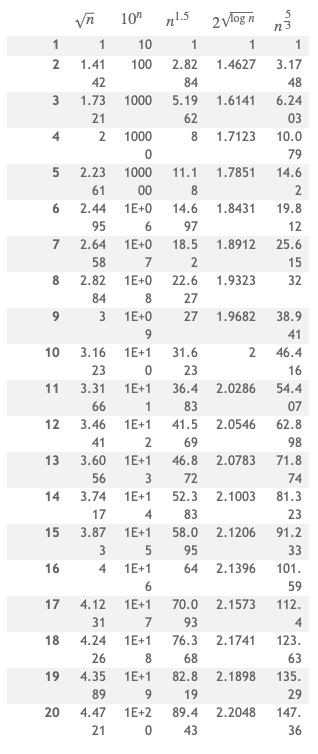
很显然答案是这样的:

实际上，我们再来看一下，取对数后（取对数不影响它们的渐进性），解决方案非常明显，所有的数取对数后

亚线性排序，有 

多项式排序，有 

指数增长是最快的 

所以排列顺序就出来了。

编码题

题目

实现课堂上的逆序对计数。

代码

def count_inversions_and_sort(array1, array2):
    """
    :param array1: 已排序的数组1
    :param array2: 已排序的数组2
    :return: (逆序对个数，排序后的合并数组)
    """
    res = []
    split_inv = 0  # 存放逆序对个数
    i = 0
    j = 0
    l1 = len(array1)
    l2 = len(array2)
    num = l1 + l2  # 总的元素个数

    for _ in range(num):
        if i == l1:  # 数组1遍历完了，只需要把数组2的剩下元素加入数组中就行
            res += [array2[x] for x in range(j, l2)]
            break
        if j == l2:
            res += [array1[x] for x in range(i, l1)]
            break

        if array1[i] < array2[j]:  # 左边的数小
            res.append(array1[i])
            i += 1
        else:
            res.append(array2[j])  # 右边的数小
            j += 1
            split_inv += (l1 - i)  # l1中所有剩余的元素

    return (split_inv, res)


def sort_and_count_inversions(array):
    """
    :param array: 需要排序的数组
    :return: (逆序对个数，排序后的数组)
    """
    if len(array) == 1:
        return (0, array)

    i = len(array) // 2  # 把数组分成左右两个部分
    l_inv, left = sort_and_count_inversions(array[0:i])  # 左逆序对
    r_inv, right = sort_and_count_inversions(array[i:])  # 右逆序对
    split_inv, merged = count_inversions_and_sort(left, right)  # 分离逆序对

    return (l_inv + r_inv + split_inv, merged)