数据结构之栈（stack）

1，栈的定义

　　栈：先进后出的数据结构，如下图所示，先进去的数据在底部，最后取出，后进去的数据在顶部，最先被取出。

　　　　　　

　　栈常用操作：　　　

s=Stack()         创建栈
s.push(item)      将数据item放在栈的顶部
s.pop()             返回栈顶部数据，并从栈中移除该数据
s.peek()           返回栈顶部数据，但不移除
s.size()            返回栈的大小
s.isEmpty()       返回栈是否为空                

　　操作示例：

　　　　　　　　　　　

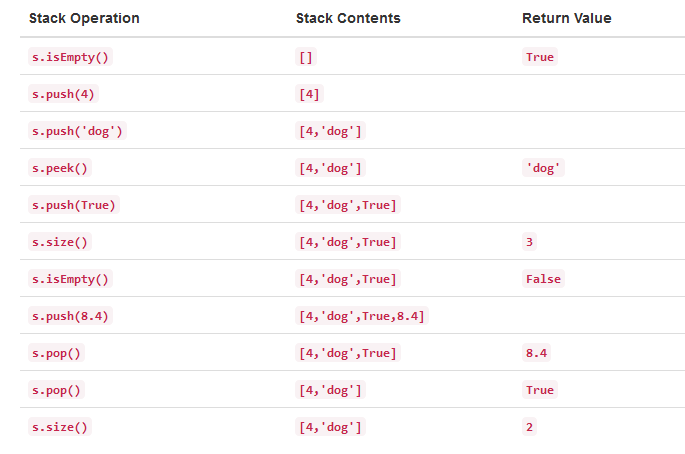
2，用python实现栈　

　　通过python的list来实现栈，其定义如下面代码所示。其中入栈和出栈操作也可以用insert(0,item)和pop(0)，但其时间复杂度为O(n)； 而append(item)和pop()时间复杂度为O(1)

class Stack(object):

    def __init__(self):
        self.items = []

    def push(self,item):
        self.items.append(item)

    def pop(self):
        return self.items.pop()

    def peek(self):
        return self.items[-1]

    def size(self):
        return len(self.items)

    def isEmpty(self):
        return self.items==[]

3, 栈的应用

　　3.1 判断单个括号是否平衡：如下图中的左括号和右括号是否依次匹配

　　　　

　　　　　　　　　　　　　　

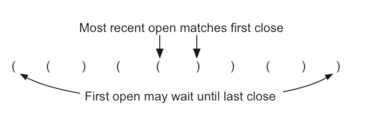
　　　　利用栈作为数据结构，左括号时入栈，右括号时出栈，相应的代码如下：

from stackDemo import Stack

parentheses = ['((((((())','()))','(()()(()','()()()','(()()']

def check_balence(pString):
    s = Stack()
    for i in range(len(pString)):
        if pString[i]=='(':
            s.push(i)
        else:
            if not s.isEmpty():
                s.pop()
            else:
                return False
    return s.isEmpty()
for pt in parentheses:
    print check_balence(pt)

　　3.2 判断多种括号是否平衡：{ [ ( 和 ) ] }应依次匹配

　　　　　　　平衡示例：

 　　　　　　

　　　　　　　不平衡示例：

　　　　　　　

　　　　实现代码如下：

from stackDemo import Stack
def check_balance(sym_string):
    s= Stack()
    for i in range(len(sym_string)):
        symbol = sym_string[i]
        if symbol in '{[(':
            s.push(symbol)
        else:
            if not s.isEmpty():
                top = s.pop()
                if not match(top,symbol):
                    return False
            else:
                return False
    return s.isEmpty()
def match(open,close):
    opens = '{[('
    closes = '}])'
    return opens.index(open)==closes.index(close)

symbols = ['{ { ( [ ] [ ] ) } ( ) }','[ [ { { ( ( ) ) } } ] ]','[ ] [ ] [ ] ( ) { }',
           '( [ ) ]','( ( ( ) ] ) )','[ { ( ) ]']

for sym_string in symbols:
　　sym_string = sym_string.replace(' ','') 
　　print check_balance(sym_string)

　　3.3. 将十进制数转化为二进制数

　　　过程：将十进制数不断除2，将余数入栈，最后再一次弹出。

　　　代码实现如下：

from stackDemo import Stack

def divideBy2(decNumber):
    s= Stack()
    while decNumber>0:
        remainder = decNumber%2
        s.push(remainder)
        decNumber = decNumber//2
    binStr = ''
    while not s.isEmpty():
        binStr = binStr + str(s.pop())
    return binStr
print divideBy2(8)

　　3.4. 将十进制数转化为二进制，八进制和十六进制数  

　　(修改代码便可以转换十进制数为任何base的数字)

from stackDemo import Stack

def baseConvetor(decNumber, base):
    s= Stack()
    while decNumber>0:
        remainder = decNumber%base
        s.push(remainder)
        decNumber = decNumber//base

    digits = '0123456789ABCDEF'   
    binStr = ''
    while not s.isEmpty():
        binStr = binStr + digits[s.pop()]
    if base==8:
        return "0"+binStr
    elif base==16:
        return "0x"+binStr
    else:
        return binStr
print baseConvetor(30,2)
print baseConvetor(30,8)
print baseConvetor(30,16)

 　　3.5 算术表达式的转换

　　　　　　一般的算术表达式顺序为Infix Expression，如下表所示，这种形式便于人类理解其执行顺序，但对于电脑，Prefix Expression 和 Postfix Expression 两种形式的表达式更容易理解。需要一个算法程序来完成Infix Expression 到 Prefix Expression 和 Postfix Expression的转换。

　　　　

　　　　Infix Expression 到 Postfix Expression的转换过程：    

　　　　　　1，新建一个stack来存放运算符，一个list来存放输出结果

　　　　　　2，对infix expression进行遍历，

　　　　　　　　当碰到运算数时将其加入到list末尾

　　　　　　　　当碰到左括号时，将其入栈，碰到右括号时，将栈中的内容依次移出并添加到list末尾，直到碰到相应的左括号停止

　　　　　　　　当碰到运算符+ - * /时，将其入栈stack，但若栈中有优先度比其高或相同的运算符，先将其移出并添加到list末尾

　　　　　　3，遍历完成后，将栈中剩余内容依次弹出，添加到list末尾

　　　　代码实现如下：

def infixtopostfix(infix):
    prec={'(':1,'+':2, '-':2, '*':3, '/':3}
    infix_list = infix.split()
    s=Stack()
    postfix_list=[]
    for item in infix_list:
        if item in "ABCDEFGHIJKLMNOPQRSTUVWXYZ" or item in "0123456789":
            postfix_list.append(item)
        elif item=='(':
            s.push(item)
        elif item==')':
            top = s.pop()
            while top!='(':
                postfix_list.append(top)
                top = s.pop()
        else:
            while not s.isEmpty() and (prec[item]<=prec[s.peek()]):
                top = s.pop()
                postfix_list.append(top)
            s.push(item)
    while not s.isEmpty():
        postfix_list.append(s.pop())
    return ' '.join(postfix_list)

print infixtopostfix("A * B + C * D")
print infixtopostfix("( A + B ) * C - ( D - E ) * ( F + G )")
print infixtopostfix("( A + B ) * C")
print infixtopostfix("( A + B ) * ( C + D )")

　　　　Postfix Expression的计算过程：

　　　　　　1，创建一个stack来存放运算数

　　　　　　2，遍历Postfix Expression

　　　　　　　　当碰到运算数时，将其入栈

　　　　　　　　当碰到运算符时，出栈两次，若第一次出栈为a，第二次出栈为b，计算 （b 运算符 a），并将结果入栈

　　　　　　3，遍历完成后，最终的计算结果在栈顶

　　　　代码实现如下：

def postfixEval(postfix):
    s = Stack()
    postfix_list = postfix.split()
    for token in postfix_list:
        if token in '0123456789':
            s.push(int(token))
        else:
            operand2 = s.pop()
            operand1 = s.pop()
            result = doMath(operand1,operand2,token)
            s.push(result)
    return s.pop()
def doMath(operand1,operand2,token):
    if token=='*':
        return operand1 * operand2
    elif token=='/':
        return operand1 / operand2
    elif token=='+':
        return operand1 + operand2
    else:
        return operand1 - operand2

print postfixEval('5 4 + 8 * 3 2 - 4 2 + * -')
print postfixEval('6 5 + 4 *')

　　　　Infix Expression 到 Prefix Expression: 将Infix Expression 翻转，左右括号互换，然后按infixtopostfix转换，最后再进行翻转？

　　　　过程示例： "( A + B ) * C" — " C * ( B + A ）"—"C B A + * "—" * + A B C"

参考：http://interactivepython.org/runestone/static/pythonds/BasicDS/WhatisaStack.html