神经网络中还有一些激活函数,池化函数,正则化和归一化函数等。需要详细看看,啃一啃吧。。
1. 激活函数
1.1 激活函数作用
在生物的神经传导中,神经元接受多个神经的输入电位,当电位超过一定值时,该神经元激活,输出一个变换后的神经电位值。而在神经网络的设计中引入了这一概念,来增强神经网络的非线性能力,更好的模拟自然界。所以激活函数的主要目的是为了引入非线性能力,即输出不是输入的线性组合。
假设下图中的隐藏层使用的为线性激活函数(恒等激活函数:a=g(z)),可以看出,当激活函数为线性激活函数时,输出不过是输入特征的线性组合(无论多少层),而不使用神经网络也可以构建这样的线性组合。而当激活函数为非线性激活函数时,通过神经网络的不断加深,可以构建出各种有趣的函数。

1.2 激活函数发展
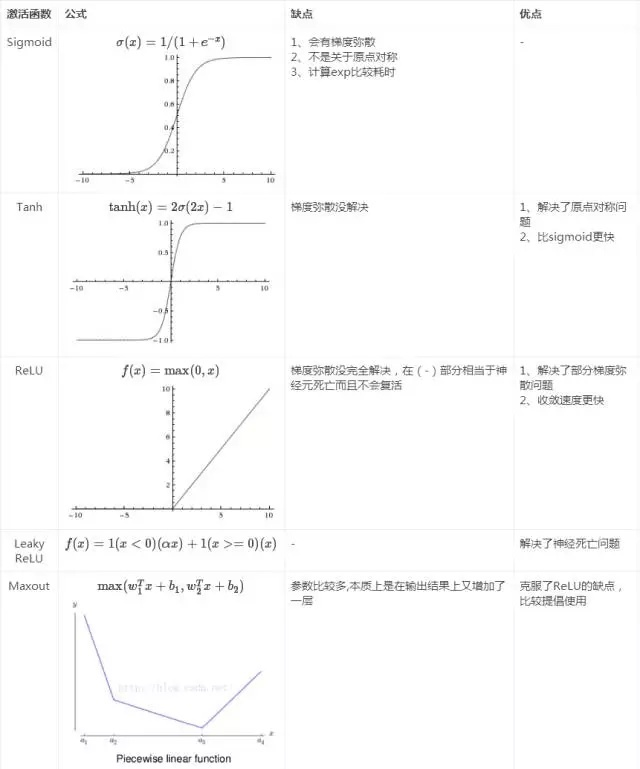
激活函数的发展过程:Sigmoid -> Tanh -> ReLU -> Leaky ReLU -> Maxout (目前大部分backbone中都采用ReLU或Leaky ReLU)。还有一个特殊的激活函数Softmax,但一般只用在网络的最后一层,进行最后的分类和归一化。借一张图总结下:
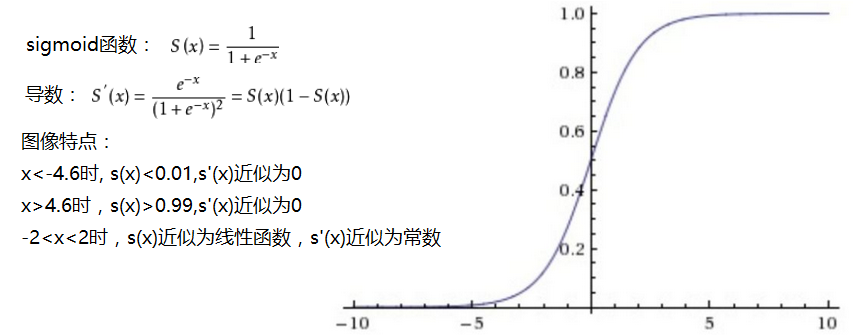
sigmoid函数:能将输入值映射到0-1范围内,目前很少用作隐藏层的激活函数,用在二分类中预测最后层输出概率值。函数特点如下:
存在问题:
- Sigmoid函数饱和使梯度消失。当神经元的激活在接近0或1处时会饱和,在这些区域梯度几乎为0,这就会导致梯度消失,几乎就有没有信号通过神经传回上一层。
- Sigmoid函数的输出不是零中心的。因为如果输入神经元的数据总是正数,那么关于
的梯度在反向传播的过程中,将会要么全部是正数,要么全部是负数,这将会导致梯度下降权重更新时出现z字型的下降。
tanh双曲正切函数:将输入值映射到-1—1范围内,目前很少用做隐藏层激活函数。
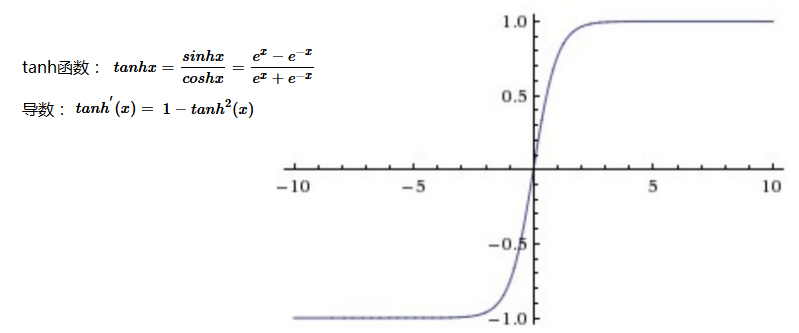
Tanh解决了Sigmoid的输出是不是零中心的问题,但仍然存在饱和问题。
(为了防止饱和,现在主流的做法会在激活函数前多做一步batch normalization,尽可能保证每一层网络的输入具有均值较小的、零中心的分布。)
ReLU函数(Rectified Linear unit):相较于sigmoid和tanh函数,计算比较简单,收敛速度较快,是目前主要的激活函数。
对比sigmoid类函数主要变化是:1)单侧抑制;2)相对宽阔的兴奋边界;3)稀疏激活性。
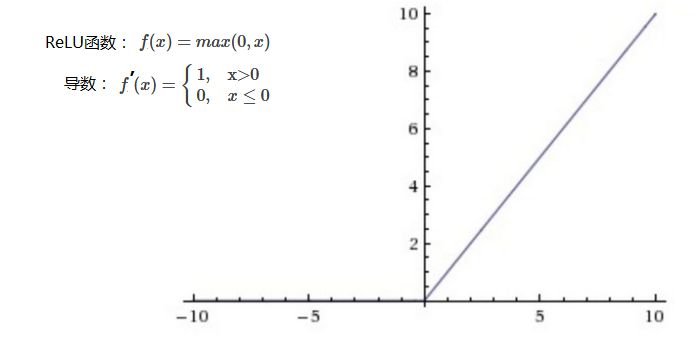
存在问题:ReLU单元比较脆弱并且可能“死掉”,而且是不可逆的,因此导致了数据多样化的丢失。通过合理设置学习率,会降低神经元“死掉”的概率。
Leaky ReLU:相比于ReLU,使负轴信息不会全部丢失,解决了ReLU神经元“死掉”的问题。
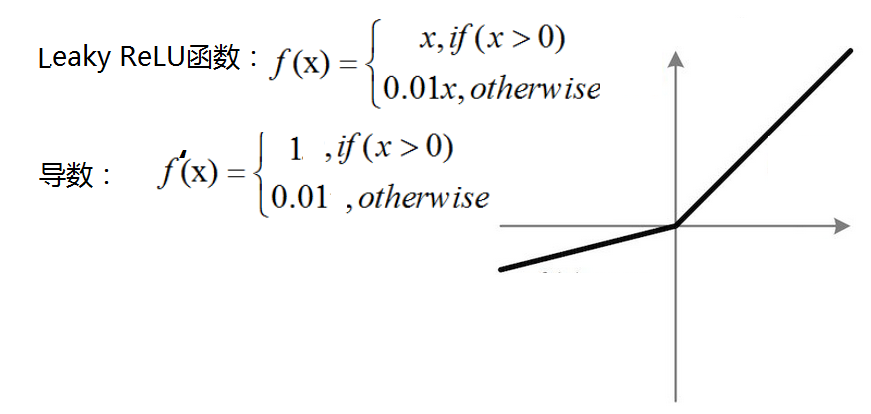
PReLU(Parametric ReLU): Leaky ReLU函数中的a,在训练过程中固定不变,常取值为0.01,而PReLU函数的a是一个学习参数,会随着梯度变化而更新。

ELUs函数(Exponential Linear Units):负半轴为指数函数,使x=0时的导数变化更加平滑


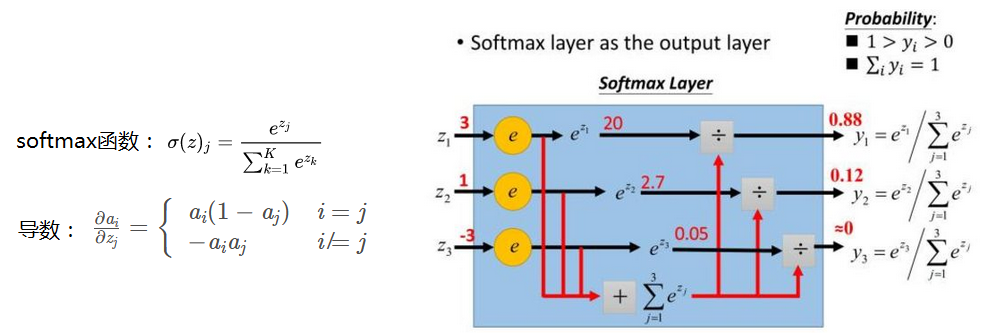
softmax: 用于多分类网络的输出,预测每一类的概率值,目的是让大的更大。
参考:https://www.jianshu.com/p/0cf1aff51117
https://www.cnblogs.com/lliuye/p/9486500.html
https://zhuanlan.zhihu.com/p/32610035
2. Batch Normalization(批量归一化)
论文:Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
2.1 背景
神经网络越深时,出现了两个问题,一是网络十分难训练,二是梯度消失。
而容易训练的数据,具有如下特征:独立同分布(Independent Identical Distribution); 不存在内部协方差偏移现象(Internal Covaraiant Shift)。
因此人们推测:在进行网络训练时,参数的变化导致每一层的输入分布会发生改变,进而上层的网络需要不停地去适应这些分布变化,使得我们的模型训练变得困难,并且这种微弱变化随着网络层数的加深而被放大(类似蝴蝶效应),这种现象便被称为Internal Covaraiant Shift。
Batch Normalization的原论文作者给了Internal Covariate Shift一个较规范的定义:在深层网络训练的过程中,由于网络中参数变化而引起内部结点数据分布发生变化的这一过程被称作Internal Covariate Shift。这句话该怎么理解呢?,我们定义每一层的线性变换为 ,其中
代表层数;非线性变换为
,其中
为第
层的激活函数。随着梯度下降的进行,每一层的参数
与
都会被更新,那么
的分布也就发生了改变,进而
也同样出现分布的改变。而
作为第
层的输入,意味着
层就需要去不停适应这种数据分布的变化,这一过程就被叫做Internal Covariate Shift。
总结Internal Covariate Shift带来的问题有两个:
(1)上层网络需要不停调整来适应输入数据分布的变化,导致网络学习速度的降低
(2)网络的训练过程容易陷入梯度饱和区,减缓网络收敛速度
(如采用饱和激活函数sigmoid时,数据分布落在了|x|>4.6的梯度饱和区域,即梯度为0)
2.2 解决思路
ICS(Internal Covariate Shift)产生的原因是由于参数更新带来的网络中每一层输入值分布的改变,并且随着网络层数的加深而变得更加严重,因此我们可以通过固定每一层网络输入值的分布来对减缓ICS问题。
(1)白化whitening: 主要是PCA白化与ZCA白化
PCA白化保证了所有特征分布均值为0,方差为1;而ZCA白化则保证了所有特征分布均值为0,方差相同。
白化是对输入数据分布进行变换,进而达到以下两个目的:使得输入特征分布具有相同的均值与方差;去除特征之间的相关性。
(2)Batch Normalization:Batch Normalization是对白化的简化版,从而减少计算量和易于实现。这是因为白化存在两个问题:
白化过程计算成本太高,并且在每一轮训练中的每一层我们都需要做如此高成本计算的白化操作
白化过程由于改变了网络每一层的分布,因而改变了网络层中本身数据的表达能力。底层网络学习到的参数信息会被白化操作丢失掉。
Batch Normalization实现算法:
(1) 白化计算量大,所以简化为对每个特征维度进行Normalization,让每个特征均值为0, 方差为1。 同时只是对每一个Mini-Batch进行Normalization
(2) 白化削弱了网络中每一层输入数据表达能力,所以Normalization后再加一个线性变换,尽可能恢复数据的表达能力。
论文中的算法公式如下:(注意求均值时是一个mini-batch上,同一个维度特征中数据的均值)

用pytorch使用了下BN方法, 并自己实现BN计算过程,代码如下:

#coding:utf-8 import torch import torch.nn as nn m = nn.BatchNorm2d(num_features=3, momentum=1) #默认的momentum=0.1,不设为1时,计算结果会和自己计算的不一样 input = torch.randn(4,3,4,4) #可以理解为batch为4, 3个channel, feature map尺寸为4*4 output = m(input) print(output) print(m.running_mean) #3个channnel的mean print(m.running_var) #3个channnel的var print(list(m.parameters())) #3个channel依次采用的γ 、β #自己计算BN weights = list(m.parameters()) output2 = torch.zeros(input.size()) me, va = [], [] for i in range(3): m = input[:, i, :, :].mean() #m1 = input[:, 0, :, :].sum()/(4*4*4), 四个batch,每个batch的feature map尺寸为4*4 v = input[:, i, :, :].var() me.append(m) va.append(v) output2[:, i, :, :] = ((input[:, i, :, :] - m)/v.sqrt()) * weights[0][i].item() + weights[1][i].item() print(output2) #和output相差0.001左右 print(me) print(va)
2.3 BN的作用
(1)BN使得网络中每层输入数据的分布相对稳定,加速模型学习速度
(2)BN使得模型对网络中的参数不那么敏感,简化调参过程,使得网络学习更加稳定
(3)BN允许网络使用饱和性激活函数(例如sigmoid,tanh等),缓解梯度消失问题
(4)BN具有一定的正则化效果
在Batch Normalization中,由于我们使用mini-batch的均值与方差作为对整体训练样本均值与方差的估计,尽管每一个batch中的数据都是从总体样本中抽样得到,但不同mini-batch的均值与方差会有所不同,这就为网络的学习过程中增加了随机噪音,与Dropout通过关闭神经元给网络训练带来噪音类似,在一定程度上对模型起到了正则化的效果。另外,原作者通过也证明了网络加入BN后,可以丢弃Dropout,模型也同样具有很好的泛化效果。
参考:https://zhuanlan.zhihu.com/p/34879333
https://zhuanlan.zhihu.com/p/24810318
3. Dropout
论文:Improving neural networks by preventing co-adaptation of feature detectors
3.1 背景
在进行神经网络的训练时,经常会出现过拟合的现象,特别是模型的参数太多,而训练样本又太少。过拟合现象表现为:训练集上损失函数较小,准确率高,测试集上损失函数大,准确率较低。而Dropout策略能在一定程度上缓解过拟合。
dropout策略:前向传播的时候,让神经元的激活值以一定的概率p停止工作,这样部分特征不会传递下去,可以使模型泛化性更强,因为它不会太依赖某些局部的特征。如下图所示:
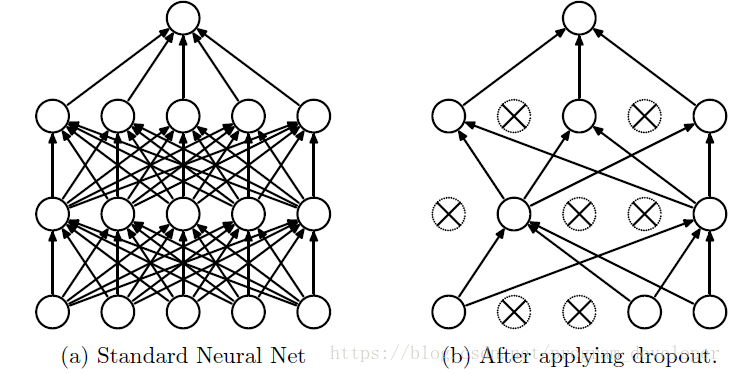
3.2 dropout算法实现
dropout算法的具体实现有两种,目前多用第二种,且概率常设置为0.5
(1)训练阶段以概率p舍弃神经元输出值,测试阶段神经元输出值乘以概率1-p。numpy实现代码如下:

#coding:utf-8 import numpy as np (1)训练阶段以概率p舍弃神经元输出值,测试阶段神经元输出值乘以概率1-p #train def dropout_train_step(x, p): zeros = np.zeros_like(x) x = np.max((zeros, input),axis=3) #ReLU mask = np.random.rand(*(x.shape)) < p #randn产生0-1的随机分布,其中值小于概率值p的为0 return x*mask #dropout,值小于概率值p的会被舍弃掉 #test def dropout_test_step(x, p): zeros = np.zeros_like(x) x = np.max((zeros, input),axis=3) #ReLU return x*(1-p) #直接乘以概率1-p, 因为每个值保留的概率值为1-p """ 由于不确定训练阶段舍弃的是那些神经元的值,测试阶段采取求期望的方式,推理如下: 假设x=[x0, x1], p=0.3; 在训练阶段的mask会出现四种情况:[0, 0], [0, 1], [1, 1], [1, 0], 每种情况的输出如下: mask=[0, 0]时, 概率为p1 = p*p=0.09, 结果为r1=[x0, x1]*[0, 0]=[0, 0] mask=[0, 1]时, 概率为p2 = p*(1-p)=0.21, 结果为r2=[x0, x1]*[0, 1]=[0, x1] mask=[1, 1]时, 概率为p3 = (1-p)*(1-p)=0.49, 结果为r3=[x0, x1]*[1, 1]=[x0, x1] mask=[1, 0]时, 概率为p4 = p*(1-p)=0.21, 结果为r4=[x0, x1]*[1, 0]=[x0, 0] 取平均值 r = (r1*p1 + r2*p2 +r3*p3 + r4*p4) = [0.7*x0, 0.7*x1] = x*(1-p) 因此在测试阶段,可以直接采用输出值乘以概率 """
由于不确定训练阶段舍弃的是那些神经元的值,测试阶段采取求期望的方式,推理如下:
假设x=[x0, x1], p=0.3; 在训练阶段的mask会出现四种情况:[0, 0], [0, 1], [1, 1], [1, 0], 每种情况的输出如下:
mask=[0, 0]时, 概率为p1 = p*p=0.09, 结果为r1=[x0, x1]*[0, 0]=[0, 0]
mask=[0, 1]时, 概率为p2 = p*(1-p)=0.21, 结果为r2=[x0, x1]*[0, 1]=[0, x1]
mask=[1, 1]时, 概率为p3 = (1-p)*(1-p)=0.49, 结果为r3=[x0, x1]*[1, 1]=[x0, x1]
mask=[1, 0]时, 概率为p4 = p*(1-p)=0.21, 结果为r4=[x0, x1]*[1, 0]=[x0, 0]
取平均值 r = (r1*p1 + r2*p2 +r3*p3 + r4*p4) = [0.7*x0, 0.7*x1] = x*(1-p)
因此在测试阶段,可以直接采用输出值乘以概率1-p
(2)训练阶段以概率p舍弃神经元输出值,并除以概率值1-p,测试阶段不处理。numpy实现代码如下:

#(2)训练阶段以概率p舍弃神经元输出值,并除以概率值1-p,测试阶段不处理 #train def dropout_train_step(x, p): zeros = np.zeros_like(x) x = np.max((zeros, input),axis=3) #ReLU mask = np.random.rand(*(x.shape)) < p #randn产生0-1的随机分布,其中值小于概率值p的为0 return x*mask/(1-p) #dropout,值小于概率值p的会被舍弃掉 #test def dropout_test_step(x, p): zeros = np.zeros_like(x) x = np.max((zeros, input),axis=3) #ReLU return x #训练阶段除以了概率1-p, 所以测试时不处理 if __name__=="__main__": input = np.random.randn(4, 3, 2, 2) print(dropout_train_step(input, 0.5))
由上面(1)可知,在测试阶段需要乘以概率1-p,可以改为在训练阶段除以概率1-p, 这样测试阶段可以的不用处理
4.正则化和归一化(Regularization and Normalization)
4.1 正则化(Regularization)
正则化(Regularization):在机器学习中,为了遏制过拟合,常使用正则化的方法。即在loss函数中引入正则化项,其实质是削弱特征值对loss的影响。
正则化形式:如下图中红色框中部分即引入的正则化项,依次为线性回归,逻辑回归和神经网络中的表示形式:

正则化原理: 下图中,对比Linear regression的正则化前后表达式,可以发现loss函数引入正则化项后,在进行梯度下降时,原参数θj 引入了一个权重(绿框部分),因此对应的输入数据对结果的影响变小了,从而削弱了特征值的影响。
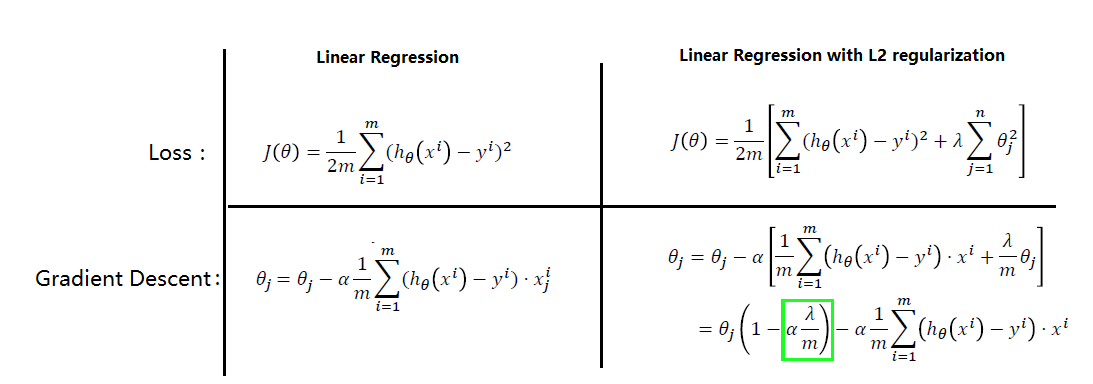
正则化种类:上述式子中都采用的是L2 Regularization,还有L1 Regularization。如下图所示:
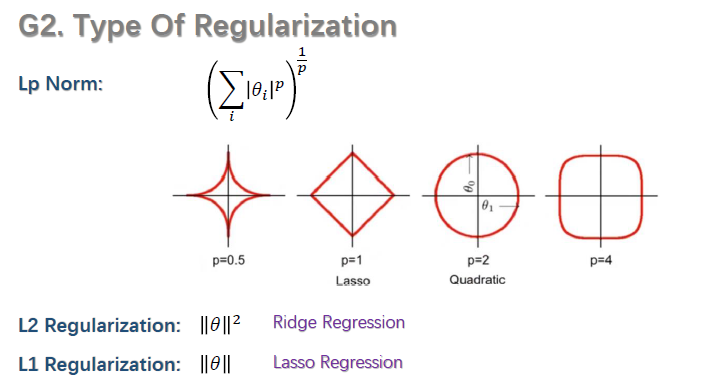
4.2 归一化(Normalization)
归一化:一条数据中常有多个特征,而每个特征维度上数据大尺度不一致,如房子有价格和房间数两个特征,价格都是过万的数字,而房间数都是十以内,差距较大,为了使其具有可比性,常在每个特征维度上进行归一化,将数据归一化到0-1范围内。归一化方法如下所示:

参考:https://www.zhihu.com/question/20924039/answer/131421690
https://www.cnblogs.com/maybe2030/p/9231231.html
