题目:
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
分析:
根据二叉树的前序和中序遍历,重建二叉树。
我们知道:
前序遍历:根节点,左子树,右子树。
中序遍历:左子树,根节点,右子树。
后序遍历:左子树,右子树,根节点。
可以发现,前序遍历的第一个数便是整个数的根节点,而这个数在中序遍历中,又将数组分成两部分,其中左边便是左子树,右边是右子树,根据划分出来的左右子树,我们又可以返回前序遍历,去查看左右子树数组中的第一个元素,这样就可以递归求解这个问题了。
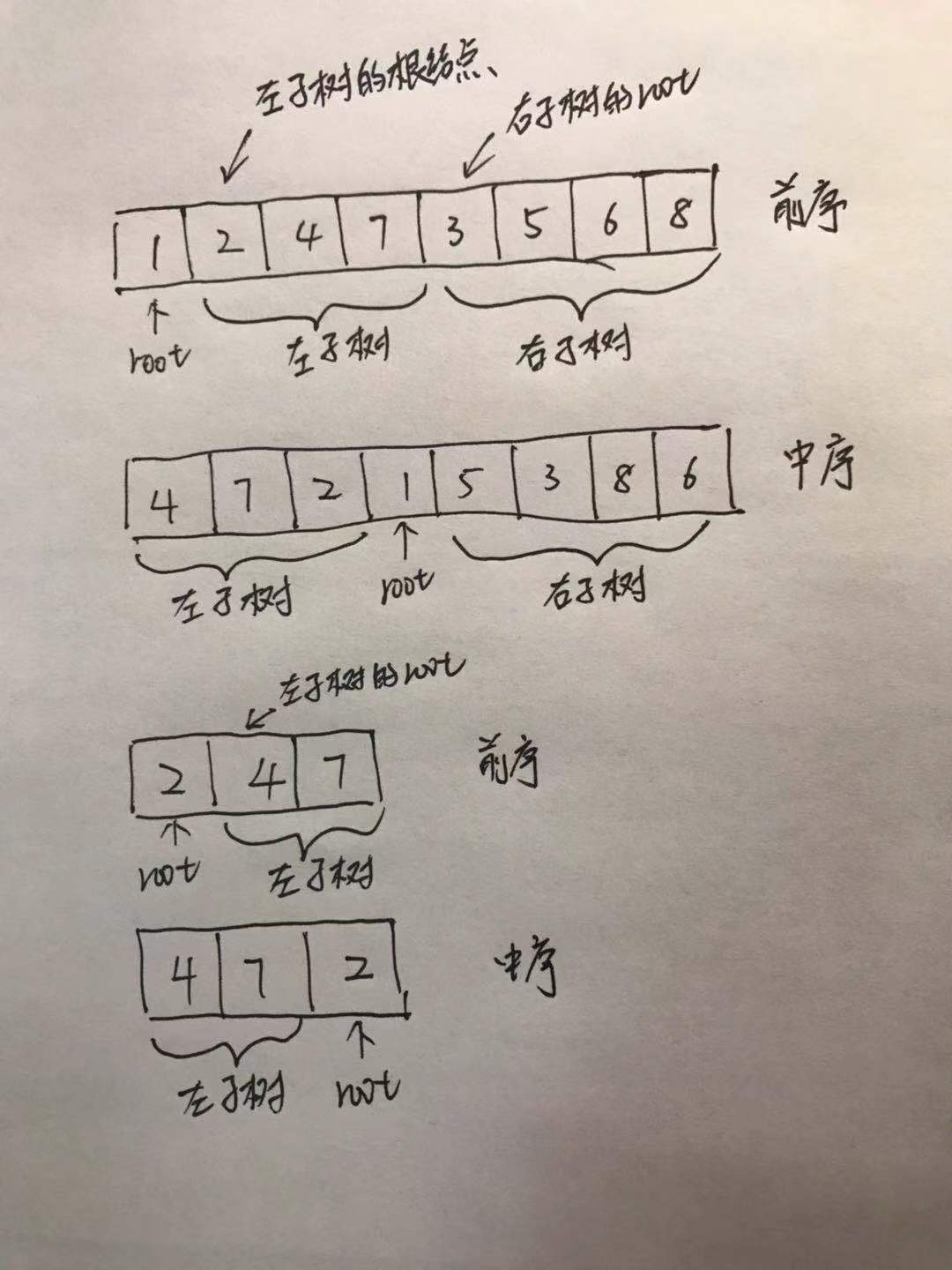
我们要记录好每次递归执行时的序列索引,这样有利于我们求解子问题需要数组的索引,前序遍历数组的左右索引记为leftPre,rightPre,中序遍历数组的左右索引是leftIn和rightIn。
则左子树的前序遍历数组左索引是leftPre+1,因为leftPre指的元素是root。
左子树的前序遍历数组右索引是leftPre+flag-leftIn,其中flag是root在中序遍历数组中的索引,而flag-leftIn正好是左子树元素的个数。
左子树的中序遍历数组索引是leftPre和flag-1,因为flag是我们找到的root元素,左边自然就是新的中序遍历数组了。
右子树的前序遍历数组左索引是leftPre+flag-leftIn+1,其实也就是左子树的右索引加1,因为在前序遍历中,左右子树是相连的。rightPre自然就成了右索引。
右子树的中序遍历数组索引是flag+1和rightIn。
不过在求解中,每次都要在中序遍历的数组中去查找根节点的索引,我们可以开始的时候将索引存进map中,需要的时候直接取,这样可以降低时间复杂度。
程序:
C++
class Solution { public: TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin) { return helper(pre, vin, 0, pre.size()-1, 0, vin.size()-1); } TreeNode* helper(vector<int>& preorder, vector<int>& inorder, int leftPre, int rightPre, int leftIn, int rightIn){ if(leftPre > rightPre) return nullptr; TreeNode* root = new TreeNode(preorder[leftPre]); if(leftPre == rightPre) return root; else{ int i = leftIn; for(;i <= rightIn; ++i){ if(inorder[i] == preorder[leftPre]) break; } root->left = helper(preorder, inorder, leftPre+1, leftPre+i-leftIn, leftIn, i-1); root->right = helper(preorder, inorder, leftPre+i+1-leftIn, rightPre, i+1, rightIn); return root; } } };
Java
//use HashMap import java.util.HashMap; public class Solution { public TreeNode reConstructBinaryTree(int [] pre,int [] in) { map = new HashMap<>(); for(int i = 0; i < in.length; ++i){ map.put(in[i], i); } return helper(pre, in, 0, pre.length-1, 0, in.length-1); } public TreeNode helper(int[] preorder, int[] inorder, int leftPre, int rightPre, int leftIn, int rightIn){ if(leftPre > rightPre) return null; TreeNode root = new TreeNode(preorder[leftPre]); if(leftPre == rightPre) return root; else{ int i = map.get(preorder[leftPre]); root.left = helper(preorder, inorder, leftPre+1, leftPre+i-leftIn, leftIn, i-1); root.right = helper(preorder, inorder, leftPre+i-leftIn+1, rightPre, i+1, rightIn); return root; } } private HashMap<Integer, Integer> map; }