-
狄利克雷分布:
是一个多维分布,一个K 维狄利克雷分布的参数是一个K维向量
 =[
=[ …
…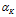 ],
],
狄利克雷分布的概率密度函数为:
 ——————————————————————1
——————————————————————1
其中 是变量,且
是变量,且 ;
; 表示伽马函数。在这里伽马函数部分充当的是归一化因子的作用。
表示伽马函数。在这里伽马函数部分充当的是归一化因子的作用。
我们把狄利克雷分布记作 。
。
2.分类分布(Categorical distribution),也叫离散分布(Discrete Distribution):
概率质量函数(分布列,相当于在连续分布中的概率密度函数)为:
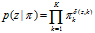 ,其中
,其中 ——————————————————2
——————————————————2
这个函数的意思就是,变量z取值为k的概率是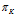 。
。
记作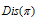 。
。
3.多项式分布:
我们从 中采样N 次,把取值为k 的样本个数记为
中采样N 次,把取值为k 的样本个数记为 ,那么随机变量
,那么随机变量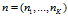 服从参数为N和
服从参数为N和 的多项式分布(Multinomial Distribution),其概率质量函数为
的多项式分布(Multinomial Distribution),其概率质量函数为
 ————————————————————————3
————————————————————————3
由以上三个分布的概率质量函数,现在以狄利克雷分布为先验(即让离散分布和多项分布中的参数π服从狄利克雷分布),在有了N个观测样本之后参数π的后验分布为:
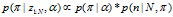
 ————————————————————————4
————————————————————————4
比较得,π的先验分布(式1)与后验分布(式4)具有相同的形式不同的参数,所以我们说狄利克雷分布是离散分布和多项式分布的共轭先验。
当我们观察到更多的样本时,只需更新后验分布的参数便可得到新的后验分布为 而不需要对π的分布进行估计。这是以狄利克雷分布作为先验的优势所在。
而不需要对π的分布进行估计。这是以狄利克雷分布作为先验的优势所在。