模式识别课堂笔记
假定用于分类的判别函数的参数形式已知，直接从样本来估计判别函数的参数。不需要有关概率密度函数的确切的参数形式。因此，属于无参数估计方法。
注：虽然判别函数有需要学习的参数，但却与前面所讲的非参数估计是一个框架下的，因为线性判别法并不关心数据的生成机理，完全由样本来确定类别情况。
分类：
线性判别函数、支持向量机、Fisher线性判别函数
广义线性判别函数、非线性判别函数、核学习机
基本思想：
步1：给定一个判别函数，且已知该函数的参数形式；
步2：采用样本来训练判别函数的参数；
步3：对于新样本，采用判别函数对其进行决策，并按照一些准则来完成分类。
技术路线：
–假定有 n 个 d 维空间中的样本，每个样本的类别标签已知，且一共有 c 个不同的类别。
–假定判别函数的形式已知，寻找一个判别函数。
–对于给定的新样本 x属于d维空间，判定它属于c中的哪个类别。
从两类分类函数入手，再设计多类问题，最后推广到广义线性模型。第二部分是关于如何训练这些函数。
1.先说二类分类函数;
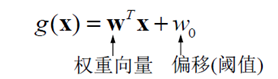
g(x)=0,定义了一个决策面H
性质：w是H 的法向量，任意一点到H的距离为
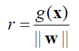这个r是有正负的，代表是否与法向量同方向。
2.接下来是多类分类:是建立在二类分类基础上的
2.1一对多情况，把第i类标记为正，其他类标记为负，这样可以构造c个二类分类面；
但是存在明显缺陷
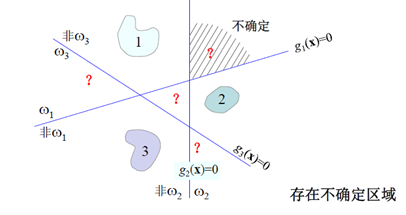
2.2一对一情况，两两进行构造分类面，构造时不考虑其他类（完全忽略），这样可以构造c(c-1)/2个分类面；
同样有缺陷，但相较于上一个不确定的区域少一点，因为分类面多了（三个的话没有效果，四个以上才有对比）
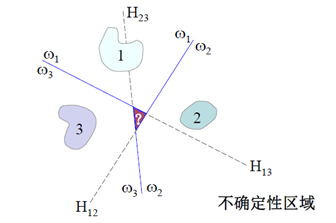
2.3对应与这种投票表决的方法有一种改进的叫最大决策的方法
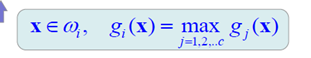
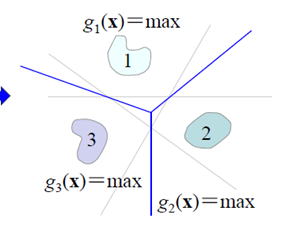
3.最后，由于线性机器有两个限制，决策区域要是凸的，而且要是单连通的。所以要对这种线性机制进行推广，得到广义线性判别函数。
原理是将低维中线性不可分的数据点x,通过非线性变化映射到高维空间中形成数据点y,以期望新的数据点y在高维空间中线性可分。
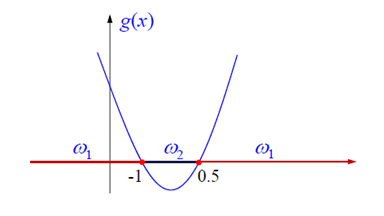
讨论完线性函数，在下一篇我们要讨论如何通过数据学习这些函数。