数据挖掘之Slope One

 计算偏差：

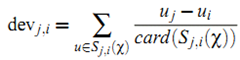
card() 表示集合包含的元素数量。

http://www.cnblogs.com/similarface/p/5385176.html

论文地址：http://lemire.me/fr/documents/publications/lemiremaclachlan_sdm05.pdf

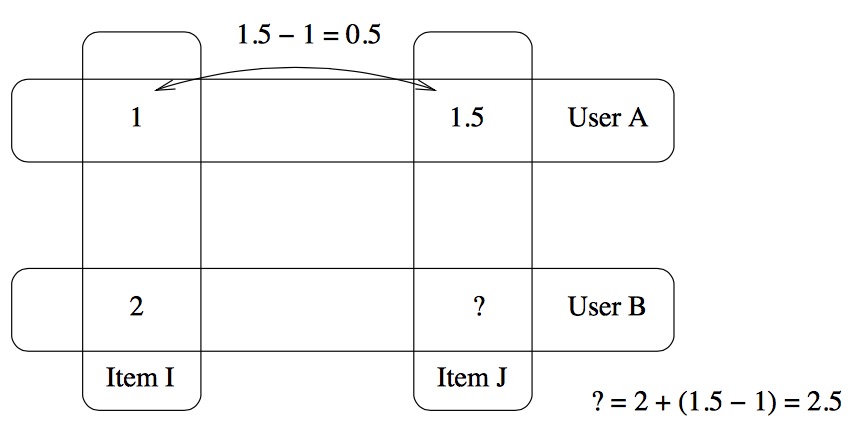
dev[itemI,itemJ]=[1.5-1]/1=0.5 这就是偏差

加权Slope One算法

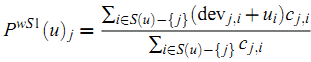
p(u)=(0.5+2)*1/1=2.5 

演绎:

	倩女幽魂	新白娘子传奇	白发魔女传
邓紫棋	4	3	4
赵丽颖	5	2	?
Angelababy	?	3.5	4
波多野结衣	5	?	3

step1:计算偏差矩阵

---

	倩女幽魂	新白娘子传奇	白发魔女传
倩女幽魂	0
新白娘子传奇		0
白发魔女传			0

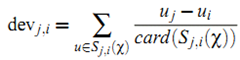
#［新白娘子传奇］到［倩女幽魂］的评分偏

dev(新白娘子传奇,倩女幽魂)=[(3-4)+(2-5)]/2=-2    {注：分母2表示同时对新白娘子传奇,倩女幽魂评分的用户数}

#［倩女幽魂］到［新白娘子传奇］的评分偏差

dev(倩女幽魂,新白娘子传奇)=[(4-3)+(5-2)]/2=2     

dev(白发魔女传,新白娘子传奇)=[(4-3)+(4-3.5)]/2=0.75

dev(白发魔女传,倩女幽魂)=[(4-4)+(3-5)]/2=-1

得到偏差矩阵：

	倩女幽魂	新白娘子传奇	白发魔女传
倩女幽魂	0	2	1
新白娘子传奇	-2	0	-0.75
白发魔女传	-1	0.75	0

step2:利用加权Slope One进行预测

---

 

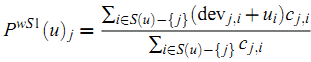
同时对i,j评分的集合

分母表示对所有除j之外用户u打过分的集合 

目标： 预测[波多野结衣]对[新白娘子传奇]的评分?

倩女幽魂 新白娘子传奇 白发魔女传
波多野结衣 5 ? 3

1. 波多野结衣 看来很喜欢“倩女幽魂” 给了5分
u(i)=5
2. 波多野结衣 她还没有看过“白娘子”，“新白娘子传奇”到“倩女幽魂” 的偏差是2
dev(j,i)=-2
3. “新白娘子传奇”和“倩女幽魂”有两个人看，哦，她们是邓紫棋 赵丽颖
c(j,i)=2
4. (dev(j,i)+u(i))*c(j,i)=(-2+5)*2=6
5. "波多野结衣" 还看了"白发魔女传" 原来绝技是学的这人的
　　u(白发魔女传)=3
6. “新白娘子传奇”到“白发魔女传” 的偏差是
　　dev(白发魔女传,新白娘子传奇)=-0.75
7. (dev(白发魔女传,新白娘子传奇)+u(白发魔女传))*2=(-0.75+3)*2=3.75*2=4.5
8. 纳尼终于 fenzi=6+4.5
9. 分母 对于每一个波多野结衣评过分的电影［"白发魔女传","倩女幽魂"］，同时对上集合和预测电影都评分的用户数的总和
　　"波多野结衣" 评分过2个电影 ［"白发魔女传","倩女幽魂"］
　　"白发魔女传"+"新白娘子传奇" = 2
　　"倩女幽魂"+"新白娘子传奇" = 2
　　于是分母＝2+2=4

10 result(波多野结衣,新白娘子传奇)=10.5/4=2.625

# coding:utf-8
__author__ = 'similarface'
'''
该数据:
{"用户":{"电影":评分}}
'''
users3 = {u"邓紫棋": {u"倩女幽魂": 4, u"新白娘子传奇": 3, u"白发魔女传": 4},
          u"赵丽颖": {u"倩女幽魂": 5, u"新白娘子传奇": 2},
          u"Angelababy": {u"新白娘子传奇": 3.5, u"白发魔女传": 4},
          u"波多野结衣": {u"倩女幽魂": 5, u"白发魔女传": 3}}

users2 = {"dzq": {"qnyh": 4, "xbnzcq": 3, "bfmnz": 4},
          "zly": {"qnyh": 5, "xbnzcq": 2},
          "Angelababy": {"xbnzcq": 3.5, "bfmnz": 4},
          "bdyjy": {"qnyh": 5, "bfmnz": 3}}

class recommender:
    def __init__(self, data, k=1, n=5):
        self.k = k
        self.n = n
        self.productid2name = {}
        if type(data).__name__ == 'dict':
            self.data = data
        #频率值 同时对A，B都进行评分的用户数目
        self.frequencies={}
        #样本A对样本B的偏差值
        self.deviations={}
    def computerDeviation(self):
        '''
        计算样本间的偏差
        :return:
        '''
        #{"用户":{"电影":评分1,"电影":评分2,"电影n":评分n}} =》 ratings={"电影":评分}
        for ratings in self.data.values():
            #"电影n":评分n
            for (item,rating) in ratings.items():
                #频率值 2样本同时都进行评分的用户数目
                #setdefault 如果键在字典中，返回这个键所对应的值。如果键不在字典中，向字典 中插入这个键，并且以{}为这个键的值，并返回{}
                self.frequencies.setdefault(item, {})
                #偏差值
                self.deviations.setdefault(item, {})
                for (item2,rating2) in ratings.items():
                    if item!=item2:
                        self.frequencies[item].setdefault(item2,0)
                        self.deviations[item].setdefault(item2,0.0)
                        self.frequencies[item][item2]+=1
                        self.deviations[item][item2]+=rating-rating2
        for (item,ratings) in self.deviations.items():
            for item2 in ratings:
                #dev(i,j)
                ratings[item2]/=self.frequencies[item][item2]

    def slopeOneRecommendations(self,userRatings):
        '''
        遍历用户u评论的所有样本：u[i]
            遍历用户u的偏差矩阵: dev[j,i]
                SUM((dev[j,i]+u[i])*c[j,i]) ==?c[j,i]=frequencies[j][i]
        :param userRatings:
        :return:
        '''
        recommendations={}
        frequencies={}
        #遍历用户u k 和 评分
        for (useritem,userRating) in userRatings.items():
            #遍历偏差矩阵
            for (diffItem,diffRatting) in self.deviations.items():
                #如果偏差矩阵的key不在用户的key中 用户的key在偏差[key]中 [新白娘子传奇 不在用户的评分中 and ["倩女幽魂","白发魔女传"] 在diffItem
                if diffItem not in userRatings and useritem in self.deviations[diffItem]:
                    #“新白娘子传奇”和“倩女幽魂”有两个人看，哦，她们是邓紫棋 赵丽颖
                    freq=self.frequencies[diffItem][useritem]
                    #
                    recommendations.setdefault(diffItem,0.0)
                    frequencies.setdefault(diffItem,0)
                    #(dev(j,i)+u(i))*c(j,i)
                    recommendations[diffItem]+=(diffRatting[useritem]+userRating)*freq
                    #求分母的和
                    frequencies[diffItem]+=freq
        recommendations=[(k,v /frequencies[k]) for k ,v in recommendations.items()]
        recommendations.sort(key=lambda artistTuple:artistTuple[1],reverse=True)
        return recommendations

if __name__ == '__main__':
    r=recommender(users2)
    r.computerDeviation()
    g=users2['bdyjy']
    result=r.slopeOneRecommendations(g)
    print(result[0][0]+' 预测评分'+str(result[0][1]))

 预测[波多野结衣]对[新白娘子传奇]的评分是2.625 

新白娘子传奇 预测评分2.625

Slope One 的算法复杂度

设有“n”个项目，“m”个用户，“N”个评分。计算每对评分之间的差值需要n(n-1)/2 单位的存储空间，最多需要 m n²步. 计算量也有可能挺悲观的:假设用户已经评价了最多 y 个项目, 那么计算不超过n²+my²个项目间计算差值是可能的。 . 如果一个用户已经评价过“x”个项目，预测单一的项目评分需要“x“步，而对其所有未评分项目做出评分预测需要最多 (n-x)x 步. 当一个用户已经评价过“x”个项目时，当该用户新增一个评价时，更新数据库需要 x步.