参考文献:https://blog.csdn.net/Dominic_S/article/details/83002153
1.硬间隔最大化


对于以上的KKT条件可以看出,对于任意的训练样本总有ai=0或者yif(xi) - 1=0即yif(xi) = 1
1)当ai=0时,代入最终的模型可得:f(x)=b,样本对模型没有贡献
2)当ai>0时,则必有yif(xi) = 1,注意这个表达式,代表的是所对应的样本刚好位于最大间隔边界上,是一个支持向量,这就引出一个SVM的重要性质:训练完成后,大部分的训练样本都不需要保留,最终的模型仅与支持向量有关。
2.软间隔最大化
如果数据加入了少数噪声点,而模型为了迁就这几个噪声点改变决策平面,即使让数据仍然线性可分,但是边际会大大缩小,这样模型的准确率虽然提高了,但是泛化误差却升高了,这也是得不偿失的。
或者有一些数据,线性不可分,或者说线性可分状况下训练准确率不能达到100%,即无法让训练误差为0。
此时此刻,我们需要让决策边界能够忍受一小部分训练误差,而不能单纯地寻求最大边际了。因为边际越大被分错的样本也就会越多,因此我们需要找出一个”最大边际“与”被分错的样本数量“之间的平衡,引入一个松弛系数ζ。
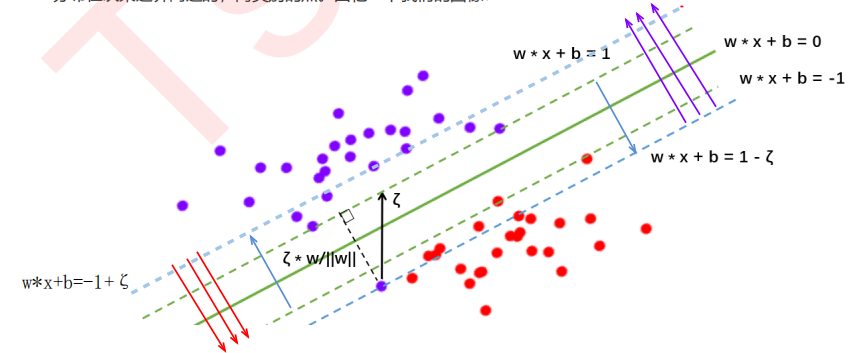
在硬间隔中:决策平面是绿色实线,约束条件是要保证两类样本点分别位于两条绿色虚线的两侧,所有样本点都被正确分类。
在软间隔中:决策平面是绿色实线,约束条件变为蓝色虚线,且红色样本点在红色箭头一侧即可,紫色样本点在紫色箭头一侧即可。
由于ζ是松弛量,即偏离绿色虚线的函数距离(绿色虚线到决策平面的距离为1),松弛量越大,表示样本点离绿色虚线越远,如果松弛量大于1,那么表示样本越过决策平面,即允许该样本点被分错。模型允许分类错误的样本数越多,模型精确性越低。因此需要对所有样本的松弛量之和进行控制,因此将所有样本量之和加入目标函数。
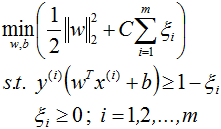
C表示的是在目标函数中松弛量的权重,C越大表示最小化时更多的考虑最小化ζ,即允许模型错分的样本越少,C值的给定需要调参。
同硬间隔最大化SVM,构造软间隔最大化的约束问题对应的Lagrange函数如下:
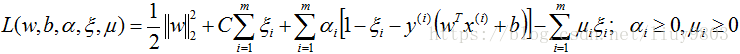
优化目标函数为: 
对偶问题为: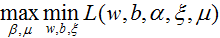

带入对偶函数得:
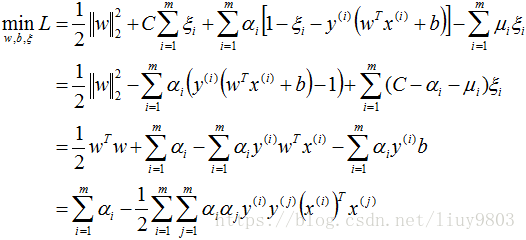
再对上式求α的极大值,即得对偶问题:
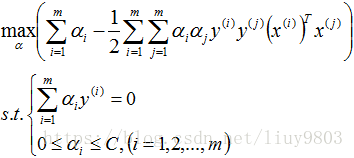
此处的约束条件由上面求导的2、3式可得。
软间隔SVM的KKT条件:
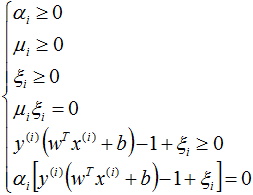
根据KKT条件中的对偶互补条件 αi(yi(wTxi+b)-1+ξi)=0 可知αi>0(即ai≠0)的样本为支持向量,在间隔边界上、间隔边界(yi(w*xi+b)=1)与决策超平面之间、或者在超平面误分一侧的向量都有可能是支持向量,因为软间隔模型中每个样本的αi、ξi不同,而αi、ξi不同的取值,样本就有可能落在不同的区域:
(1)αi<C,则μi>0,ξi=0,支持向量xi恰好落在间隔边界上;
(2)αi=C,则μi=0,则ζ≠0
0<ξi<1,则分类正确,xi在间隔边界与决策超平面之间;
ξi=1,则xi在决策超平面上;
ξi>1,则xi位于决策超平面误分一侧。
求得的每个样本点的α和ζ都不同,因此那条有松弛量的蓝色虚线超平面只是一个抽象概念,是不存在的,因为各个样本的松弛量都不同,C只是对总体样本的松弛量(即误差进行控制)。
支持向量是满足yi(w*xi+b)=1-ζi这个式子的样本,因为每个样本的ζi不同因此支持向量构不成线。间隔边界yi(w*xi+b)=1还在原来的地方。
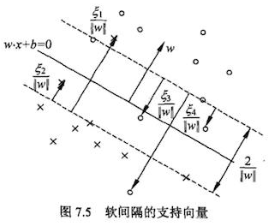
图中箭头所指的样本点都可以是支持向量。
如果给定的惩罚项系数C越小,在模型构建的时候就允许存在越多分类错误的样本,也就是表示此时模型的准确率比较低;如果给定的C越大,表示在模型构建的时候,允许分类错误的样本越少,也就表示此时模型的准确率比较高。