研究动机
异构信息网络是推荐系统中重要的数据表示。异构信息网络的推荐系统常常面临2个问题：如何去表示推荐系统的高级语义，如何向推荐系统中融入异构信息。在这篇文章中，我们首先将meta-graph融入到HIN-based推荐系统中，然后利用”MF+FM“的方法求解信息融合问题。对于每个meta-graph生成的相似性，利用MF的方法进行生成用户的潜在特征和项目的潜在特征。针对不同的mate-graph特征，我们提出了一种基于群lasso正则化的FM方法，去自动从观察到的信息中有效的选择有效的meta-graph方法。
传统的模型
为了结合丰富的语义，HIN首先构建异构网络的网络模式。比如，在Yelp中，网络模式是在实体类型上定义的 User，Review，Word，Business，然后，受实体类型约束的语义关联可以通过元路径上两个实体之间的相似性来定义。对于传统的协同过滤推荐，如果我们想把business推荐给用户，我们可以建立一个简单的meta-path Business->User然后从这个元路径中进行学习。同时，在异构网络中，我们也可以定义更复杂的meta-path，比如 User->Review -> Word -> Review -> Business, 这个meta-path定义了如果用户与其他用户对相同的Business进行了相似的评论，以度量用户是否倾向于喜欢某个业务。
存在的挑战
- 元路径可能不是描述丰富语义的最佳方法，所以可以采用meta-graph，相比 meta-path 要求必须是 sequence 的结构，meta-graph 只要求「一个起点和一个终点，中间结构并不限制」
- 不同的meta-path和不同的meta-graph会导致不同的相似性，如果有效的结合它们，是另一个挑战。考虑到我们最终的目标是生成一个user-item评分矩阵，所以可以将其考虑为一个矩阵补全问题，所以，解决的方法有两种：
- 第一种：使用meta-path生成大量的备选相似度，然后学习不同元路径的加权机制，将相似性显式地结合起来，逼近观察到的用户-项目评价矩阵，这种方法没有考虑jmeta-path的隐式因素，每个可选的相似矩阵可能非常稀疏，从而有助于最终的集成。
- 第二种：对每个元路径计算的用户项相似矩阵进行因子分解，然后利用潜在特征恢复一个新的用户项矩阵。然而这种方法不太好，因为每个meta-path不能看到其他的变量，只能看到其他变量预测出来的单个值。
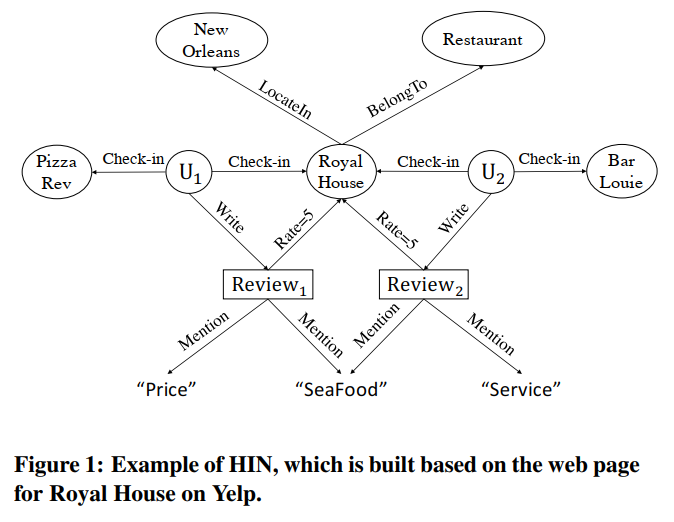
面对以上的挑战，作者想到了一个新的结合方法，来充分的结合不同的潜在特征。
- 不使用meta-path，而是使用meta-graph，将更复杂的语义信息融入到我们的预测问题之中
- 没有直接的去计算recovered矩阵，而是使用了所有meta-graphs的潜在特征。对于每一个meta-graph，我们首先计算user-item的相似度矩阵，然后利用MF方法，分解成user 和 itemde 潜在向量。然后从不同的meta-graph获取到不同的user 和 item 向量，并利用FM把它们组装起来。
通过这种方式，我们可以自动确定应该使用哪个元图来解决新出现的问题，以及对于生成的每个元图用户和项向量，应该如何对它们进行加权。
模型框架
基于meta-graph的相似度
Meta-graph的定义如下
作者写出了所有的meta-graph，我们可以看到所有的U(User)为源节点，B(Business)为目标节点。
根据以上的定义，我们需要计算源节点和目标节点的相似性。
commuting matrices [32] have been used to compute the counting based similarity matrix of a meta-path。
可交换矩阵维基百科定义
假设我们有一个meta-path，
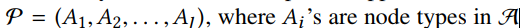
这时我们可以定义一个矩阵$W_{A_iA_j}$作为$A_i$和$A_j$的邻接矩阵。然后路径$P$的可交换矩阵（the commuting matrix）为
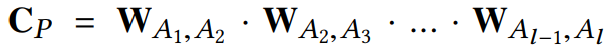
如何去计算meta-graph的可交换矩阵
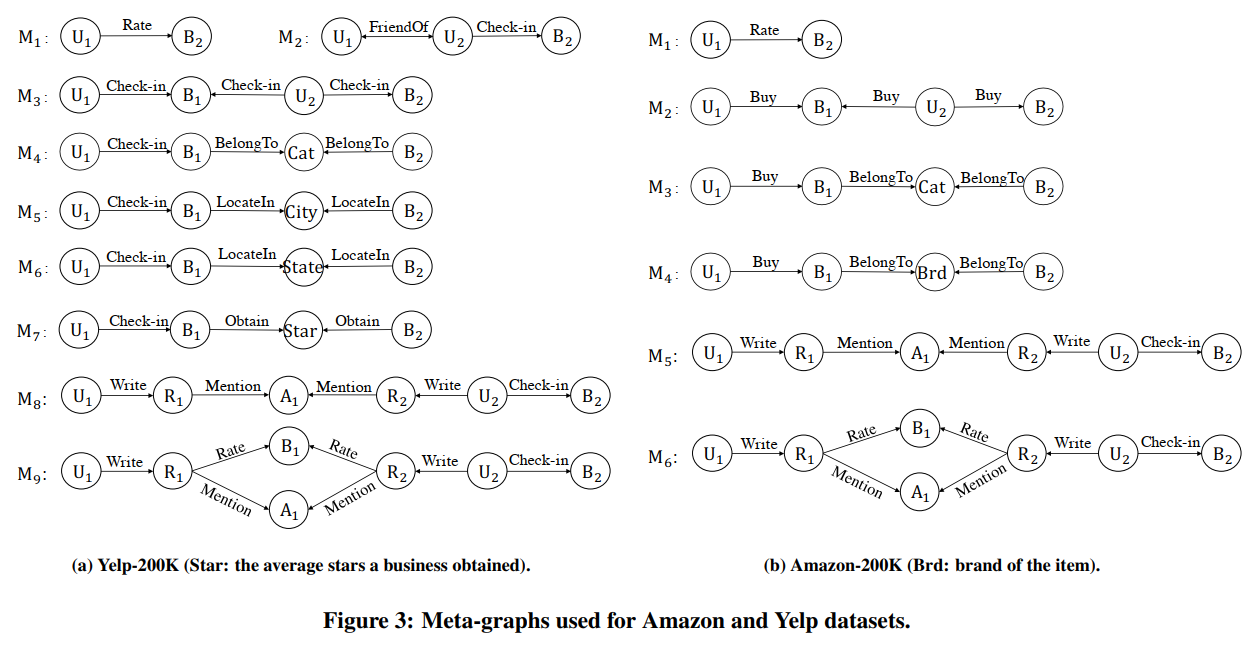
利用meta-graph计算完所有的users和item的相似度之后，我们就可以获得一个相似度矩阵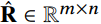
，其中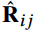
表示user $u_i$和item $b_j$在meta-graph下的相似度，其中$m$和$n$是users和items的数量。如果设计了L个meta－graph，那么就是L个个不同的user-item相似度矩阵，它们的表示为
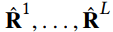
基于meta-graph的潜在特征
利用矩阵分解的方法，得到user和item的低维表示为
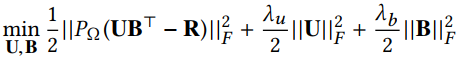
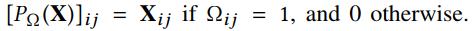
在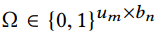
中被观察到的位置用1表示， $lambda_u$和$lambda_b$是正则项，防止过拟合。
对于L个基于meta-graph的用户与项目之间的相似性，我们可以得到L组用户与项目的潜在特征，记为
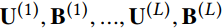
推荐模型
我们可以得到L组特征，每组的维度为$F$（在矩阵分解的时候，我们设定秩为$F$），那么我们就可以拼出一个维度为$2LF$的特征向量。
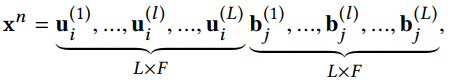
$x^n$表示的是连接后的第n个样本的特征向量。利用FM的方法
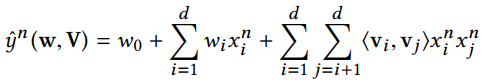
利用Least Squared loss
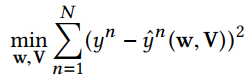
但是利用FM模型存在两个问题
第一个：在处理多个meta-graph的时候可能会产生噪音，进而影响模型的预测能力。此外，在实践中，一些元图可能是无用的，因为一些元路径提供的信息可以被其他元路径覆盖
第二个：计算的开销过大，计算学习模型参数和在线推荐参数的成本很大
为了解决以上2个问题，我们使用了Group Lasso 分组最小角回归算法，参数$p$的定义如下：
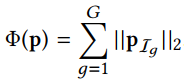
与以往基于潜在特征的模型进行了比较
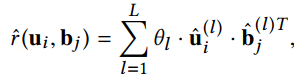
$L$表示的是meta-path的数量，$ heta_l$是第$l$个meta-path的权重，这里的预测方法是不够的，因为它不能捕捉到元图特征之间的交互，它可能会降低所有用户和项目特性的预测能力。
模型优化
目标函数
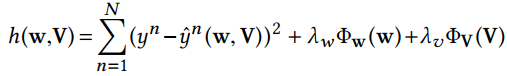
使用 group lasso 正则项之后，目标函数优化就变成了一个非凸非光滑（non-convex, non-smooth）的问题，我们使用了邻近梯度算法（proximal gradient）算法来求解它，采用的是nmAPG算法。使用的动机：
首先，非光滑性来自于所提出的正则化器，由于相应的近似步骤具有廉价的闭形式解，因此可以有效地处理。
其次，加速技术对于显著加快一阶优化算法的速度非常有用，而nmAPG是唯一能够处理一般非凸问题且具有良好收敛保证的技术。
实验
Baseline
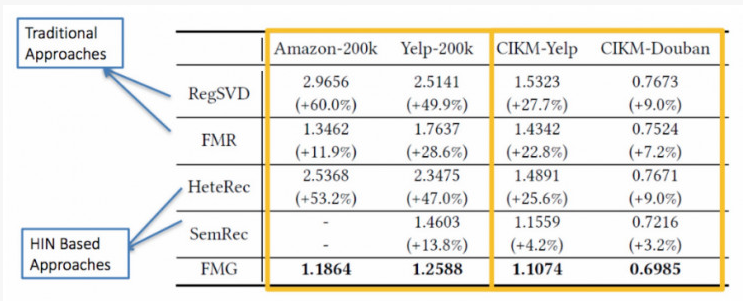
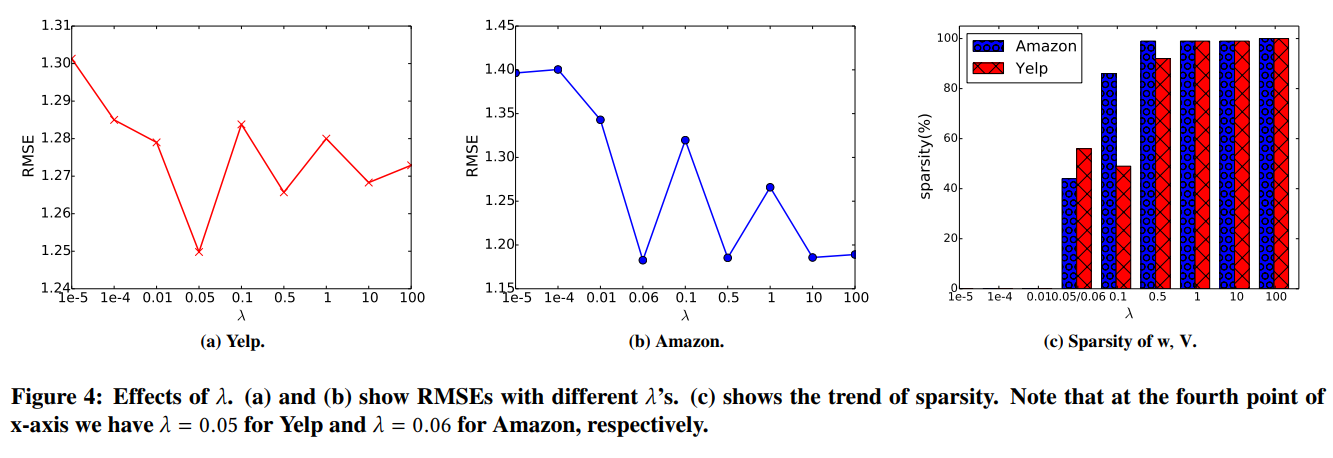
参数$lamda$
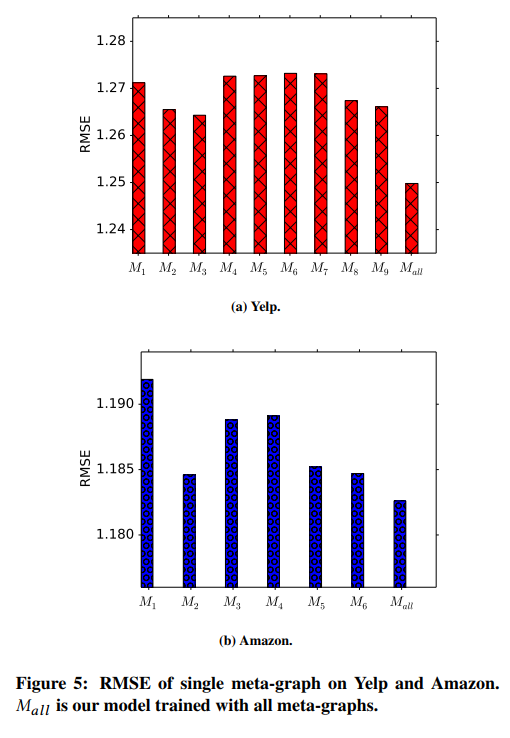
Recommending Performance with Single Meta-Graph
参数F和K
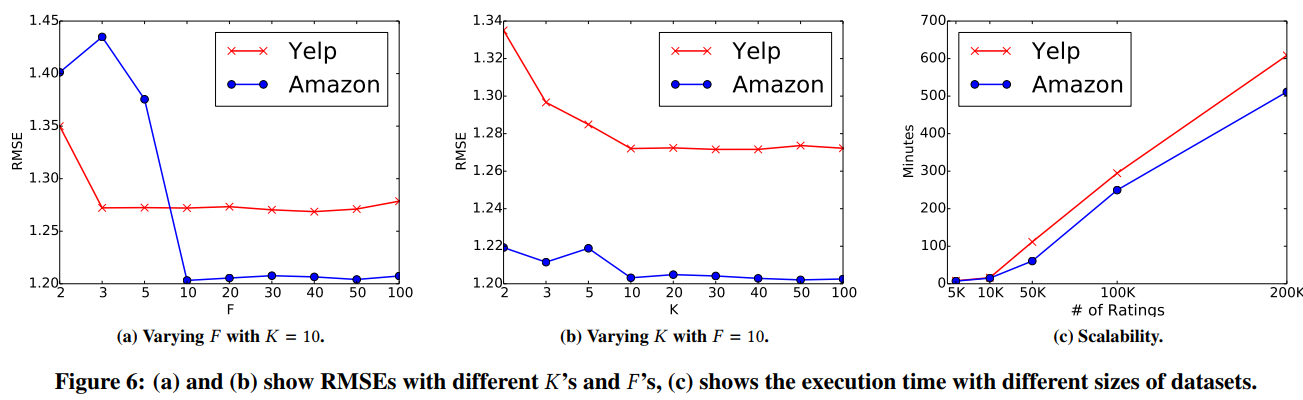
总结
该模型利用meta-graph提取复杂的语义关系，利用MF对user和item提取潜在特征，利用group lasso正则化的FM进行对不同meta-graph中提取的不同组语义信息进行融合，进而预测。