题意:
已知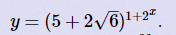 ,给你整数x,和一个素数M,求[y]%M
,给你整数x,和一个素数M,求[y]%M
思路:
设
(5+2√6)n=Xn+Yn*√6
Xn+Yn*√6 =(Xn-1+Yn-1*√6)*(5+2√6)
=> 5*Xn-1 + 12*Yn-1 + (2*Xn-1 + 5*Yn-1 )*√6
Xn = 5*Xn-1 + 12*Yn-1;
Yn = 2*Xn-1 + 5*Yn-1;

然而√6还是一个大问题,解决办法:
(5 - 2√6)n = Xn - Yn*√6
(5+2√6)n=Xn+Yn*√6 + Xn - Yn*√6 - (Xn - Yn*√6) = 2*Xn - (0.101)n
所以[ (5+2√6)n ]= 2*Xn - 1
由于n=1+2^x 是一个非常大的数,这时我们要知道广义斐波那契数列的循环节是(MOD-1)*(MOD+1)
代码:
#include <cstdio> #include <iostream> #include <cmath> #include <algorithm> #define ll long long using namespace std; const int N=2,M=2,P=2; ll MOD; struct Matrix { ll m[N][N]; }; Matrix A= {5,12, 2,5 }; Matrix I= {1,0, 0,1 }; Matrix multi(Matrix a,Matrix b) { Matrix ans; for(int i=0; i<N; i++) { for(int j=0; j<M; j++) { ans.m[i][j]=0; for(int k=0; k<P; k++) { ans.m[i][j]+=a.m[i][k]*b.m[k][j]%MOD; } ans.m[i][j]%=MOD; } } return ans; } Matrix power(Matrix a,ll k) { Matrix ans=I,p=a; while(k) { if(k&1) { ans=multi(ans,p); } k=k/2; p=multi(p,p); } return ans; } ll qmod(ll a,ll b,ll mod) { ll ans=1; a=a%mod; while(b) { if(b&1) { ans=(ans*a)%mod; } b=b/2; a=(a*a)%mod; } return ans; } int main(int argc, char const *argv[]) { int t,cas=1,n; cin>>t; while(t--) { cin>>n>>MOD; cout<<"Case #"<<cas++<<": "; n=qmod(2,n,(MOD*MOD-1))+1; Matrix ans=power(A,n-1); ll xn=(5*ans.m[0][0]+2*ans.m[0][1])%MOD; cout<<(2*xn-1)%MOD<<endl; } return 0; }